1.图
1.1 图的定义
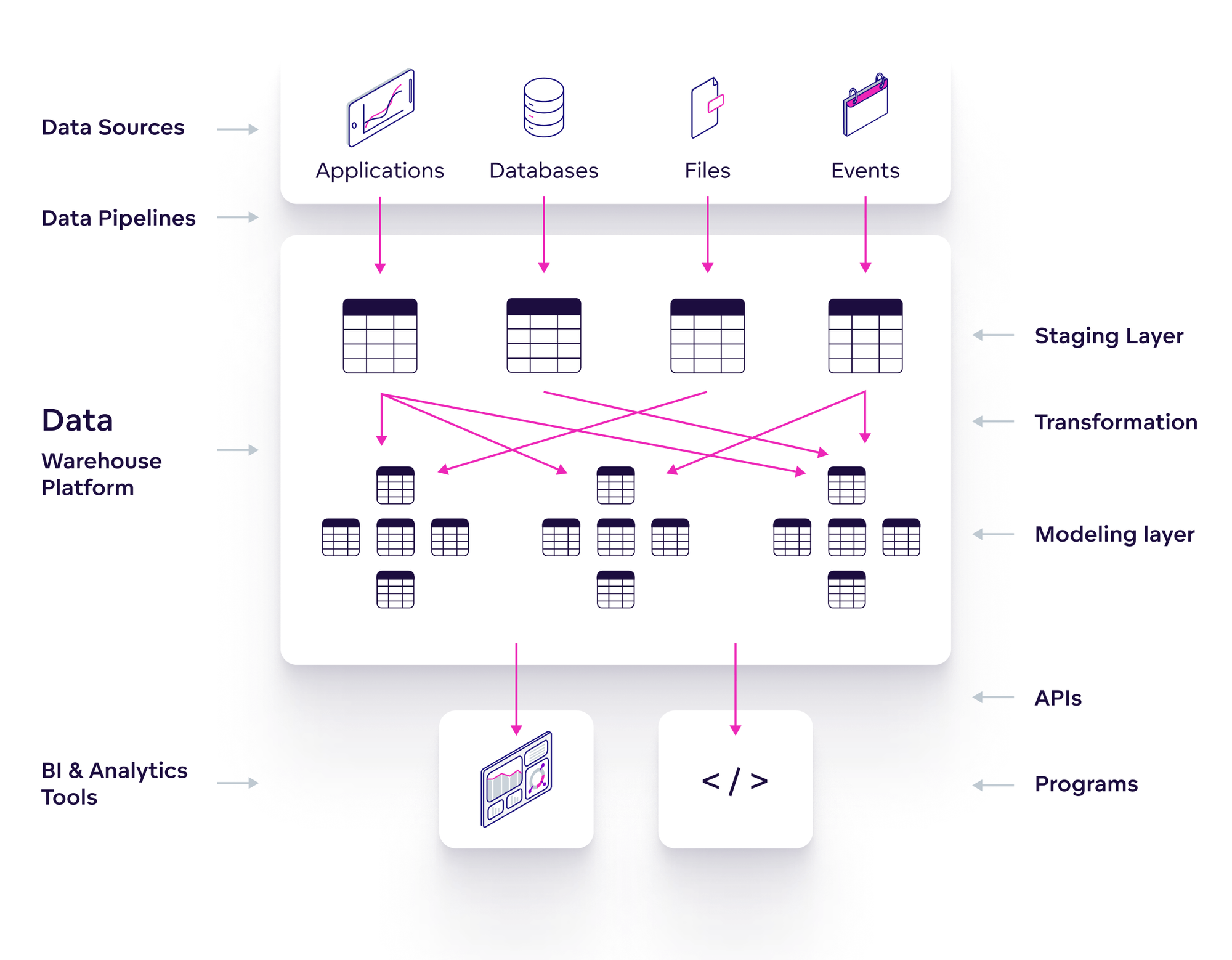
图是由节点(顶点)和边构成的数学结构。图用于表示对象之间的关系,其中节点表示对象,边表示对象之间的关系。

一个图,记为 G = <V, E> ,它包括以下两个要素:
1.节点(顶点)(Vertices):表示图中的对象或实体。通常用 V = {v1, v2, v3, …} 表示图的节点集合。
2.边(Edges):表示对象之间的关系。通常用E = {e1, e2, e2, …}表示图的边集合。也可用两个节点表示 E = {( v1, v2), (v2, v3), (v3, v4), …}
例如,一个简单的无向图,其中包含一些城市和它们之间的道路。表示为二元组 G = (V, E),其中:
- V = {a, b, c, d, e} 是城市的集合,分别代表着城市a, b, c, d, e 。
- E = { (a, b), (a, c), (b, d), (c, d), (d, e) } 是道路的集合,每一对表示一条连接的道路。
节点和边的信息可以是类别型,数值型的,例如:

1.2 图的类型
根据节点和边等特征,图可以分为不同类型:
- 有向图(Directed Graph):边有方向,从一个节点指向另一个节点。
- 无向图(Undirected Graph):边没有方向,表示对等关系。
- 加权图(Weighted Graph):边具有权重,代表关系的强度或成本。记为点 𝑣𝑖 到 𝑣𝑗 的权重为 𝑤𝑖𝑗.
- 无权图(Unweighted Graph):边没有权重。
- 简单图(Simple Graph):每对节点之间最多只有一条边,且没有自环。
- 多重图(Multigraph):允许多条边连接相同的节点。
- 连通图(Connected Graph):所有节点都可以通过路径连接到其他节点。
- 非连通图(Disconnected Graph):存在至少一个孤立节点或子图。
2.Python创建图
安装networkx库:
pip install -i https://pypi.tuna.tsinghua.edu.cn/simple networkx
networkx的中文教程 — NetworkX 2.8 文档![]() https://www.osgeo.cn/networkx/tutorial.html创建图的基本步骤
https://www.osgeo.cn/networkx/tutorial.html创建图的基本步骤
- 导入NetworkX:首先,导入NetworkX库。
- 创建图:可以创建一个空图,或通过数据结构(如列表、字典)直接构建图。
- 添加节点:使用
add_node()或add_nodes_from()添加单个或多个节点。 - 添加边:使用
add_edge()或add_edges_from()添加单个或多个边。 - 操作图:可以查询节点和边、计算图的属性、执行算法等。
2.1 创建一个图:
python">import networkx as nx
import matplotlib.pyplot as plt# 创建一个空图
G = nx.Graph()# 添加节点
G.add_nodes_from([1, 2, 3, 4, 5])# 添加边
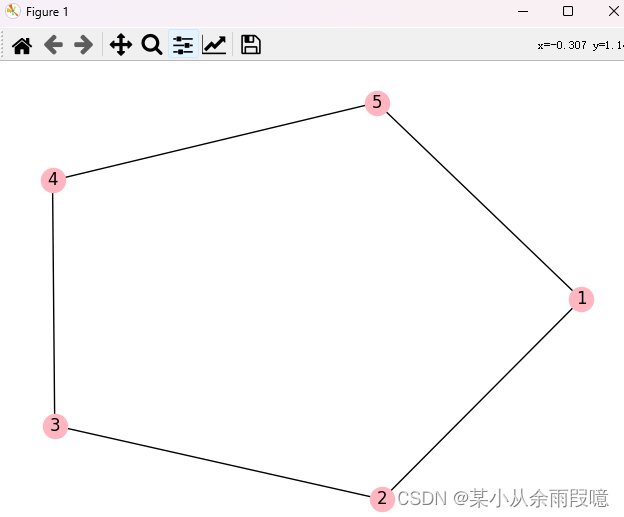
G.add_edges_from([(1, 2), (2, 3), (3, 4), (4, 5), (5, 1)])# 绘制图
nx.draw(G, with_labels=True, node_color='lightpink')
plt.show()输出:
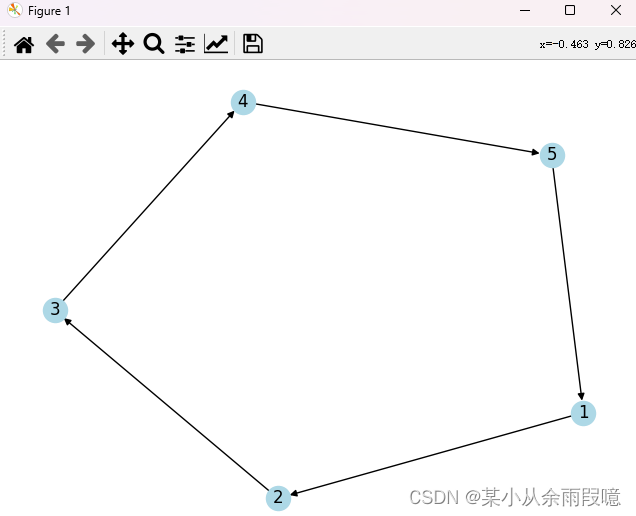
3.2 创建有向图:
python"># 有向图
import networkx as nx
import matplotlib.pyplot as plt# 创建一个空的有向图
G = nx.DiGraph()# 添加节点
G.add_nodes_from([1, 2, 3, 4, 5])# 添加有向边
G.add_edges_from([(1, 2), (2, 3), (3, 4), (4, 5), (5, 1)]) # 这些边是有方向的# 绘制有向图
# with_labels:是否有节点标签,node_color:节点的颜色
nx.draw(G, with_labels=True, node_color='lightblue', arrowstyle='-|>')
plt.show()输出:
2.3 创建有权图:
python"># 创建一个空的加权图
WG = nx.DiGraph() # 也可以是 nx.Graph(),取决于是否需要有向# 添加节点
WG.add_nodes_from([1, 2, 3, 4, 5])# 添加加权边
WG.add_edge(1, 2, weight=0.5)
WG.add_edge(2, 3, weight=1.2)
WG.add_edge(3, 4, weight=0.8)
WG.add_edge(4, 5, weight=1.5)
WG.add_edge(5, 1, weight=2.0)# 绘制加权图
# 使用边权重进行可视化
edge_labels = nx.get_edge_attributes(WG, 'weight')nx.draw(WG, with_labels=True, node_color='lightgreen', arrowstyle='-|>')
nx.draw_networkx_edge_labels(WG, pos=nx.spring_layout(WG), edge_labels=edge_labels)
plt.show()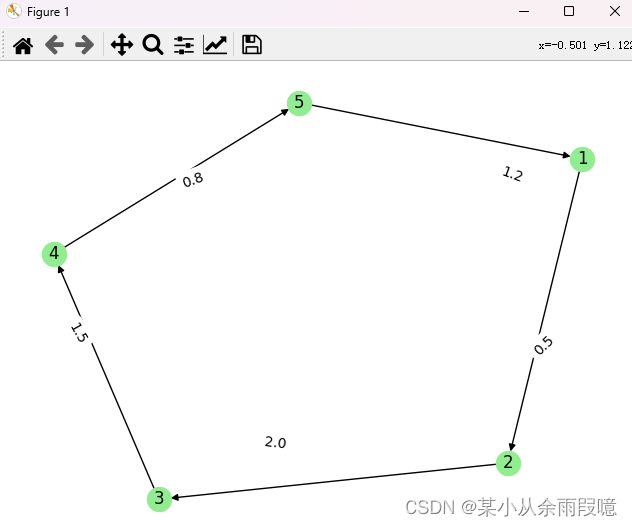
3.图的性质
3.1 邻接节点(neighbors)
- 节点 𝑣𝑖 的邻接节点是与节点 𝑣𝑖 直接相连的节点,其被记为 𝑁(𝑣𝑖)。
- 节点 𝑣𝑖 的 𝑘 跳远的邻接节点(neighbors with 𝑘-hop)是到节点 𝑣𝑖 要走 𝑘 步的节点(一个节点的 2 跳远的邻接节点包含了自身)。
3.2 图的度(degree)
一个顶点在图中的度 (degree)为与这个顶点相连接的边的数目。
如下图,武则天的度为6,上官婉儿的度为1。

在无向图中,节点的度表示与该节点直接相连的边的数量:
- 度(Degree):无向图中节点的度是连接到该节点的边的数量。度越高,表示该节点越活跃。
- 平均度:整个图中所有节点的平均度。
- 最大度和最小度:图中节点的最高和最低度。
在有向图中,度分为两种:入度和出度:
- 入度(In-degree):指向某个节点的边的数量,表示有多少条边进入该节点。
- 出度(Out-degree):从某个节点发出的边的数量,表示有多少条边从该节点出去。
- 总度(Total degree):入度和出度的总和。
我们使用一个 NetworkX 中自带的图 The Karate Club Network(空手道俱乐部网络)进行学习。空手道俱乐部网络描述了空手道俱乐部 34 名成员的社交网络,并记录了在俱乐部外互动的成员之间的链接。
python"># 创建一个空手道俱乐部网络
G = nx.karate_club_graph()# G 是否是一个有向图
print(type(G))# 可视化图
nx.draw(G, with_labels = True, node_color='Gold')
plt.show()# 计算了每个节点的度,接着计算了度的总和,并用节点数量求平均
# 获取所有节点的度
degrees = dict(G.degree())# 计算平均度
average_degree = sum(degrees.values()) / len(degrees)
print("空手道俱乐部网络的平均度是:", average_degree)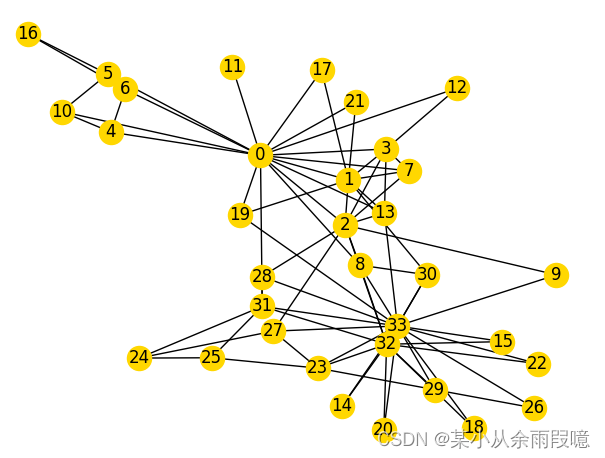
![]()
3.3 行走(walk)和路径(path)
- 𝑤𝑎𝑙𝑘(𝑣1,𝑣2)=(𝑣1,𝑒6,𝑒5,𝑒4,𝑒1,𝑣2),这是一次“行走”,它是一次从节点 𝑣1 出发,依次经过边 𝑒6,𝑒5,𝑒4,𝑒1,最终到达节点 𝑣2 的“行走”。
- 下图所示为 𝑤𝑎𝑙𝑘(𝑣1,𝑣2)=(𝑣1,𝑒6,𝑒5,𝑒4,𝑒1,𝑣2),其中红色数字标识了边的访问序号。
- 在“行走”中,节点是允许重复的。
- 路径是节点不可重复的行走。

3.4 节点间的距离和图的直径
节点距离(distance)指的是在图中两个节点之间的最短路径长度(shortest path)。对于无向图和有向图的距离计算略有不同:
- 无向图:节点之间的距离是指通过最少的边连接这两个节点的路径长度。
- 有向图:节点之间的距离是指沿着方向连接这两个节点的最短路径长度。
在NetworkX中,计算节点距离的方法有:
shortest_path_length(G, source, target): 计算两个特定节点之间的最短路径长度。all_pairs_shortest_path_length(G): 计算所有节点对之间的最短路径长度。
直径(diameter):给定一个连通图 𝐺={𝑉,𝐸}G={V,E},其直径为其所有节点对之间的最短路径的最大值。
python"># 创建一个简单的无向图
G = nx.Graph()
G.add_edges_from([(1, 2), (1, 3), (2, 3), (3, 4), (4, 5), (1, 5)])nx.draw(G, with_labels = True, node_color='LightGreen')
plt.show()# 计算两个节点之间的最短路径长度
distance_1_3 = nx.shortest_path_length(G, source=1, target=3)
distance_1_4 = nx.shortest_path_length(G, source=1, target=4)# 计算图的直径
graph_diameter = nx.diameter(G)print("节点 1 和 3 之间的距离:", distance_1_3)
print("节点 1 和 4 之间的距离:", distance_1_4)print("图的直径:", graph_diameter)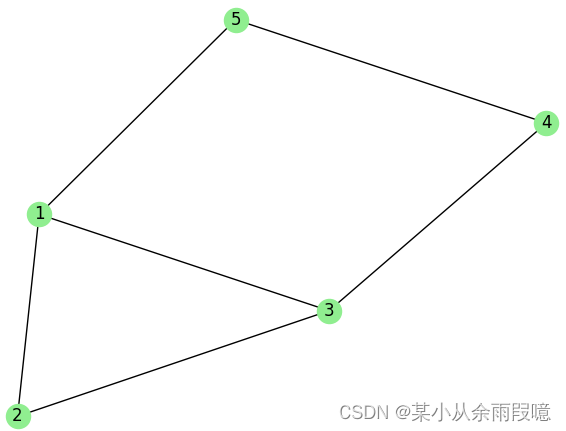

3.5 子图、连通分量,连通图
子图(Subgraph)
子图是从一个图中选择部分节点和边组成的新图。子图保留原始图中的连接关系,但通常包含更少的节点和边。
子图可以基于特定条件来构建,例如选择特定的节点或边。在NetworkX中,可以使用 subgraph() 方法从一个图中提取子图。例如:
python"># 创建一个空手道俱乐部网络
G = nx.karate_club_graph()# 可视化完整的空手道俱乐部网络
nx.draw(G, with_labels=True, node_color='Gold', edge_color='gray')
plt.show()# 创建子图,包括节点 0 到 5 及其连接的边
sub_G = G.subgraph([0, 1, 2, 3, 4, 5])# 可视化子图
nx.draw(sub_G, with_labels=True, node_color='lightgreen', edge_color='blue')
plt.show()# 打印子图中的节点和边
print("子图中的节点:", list(sub_G.nodes()))
print("子图中的边:", list(sub_G.edges()))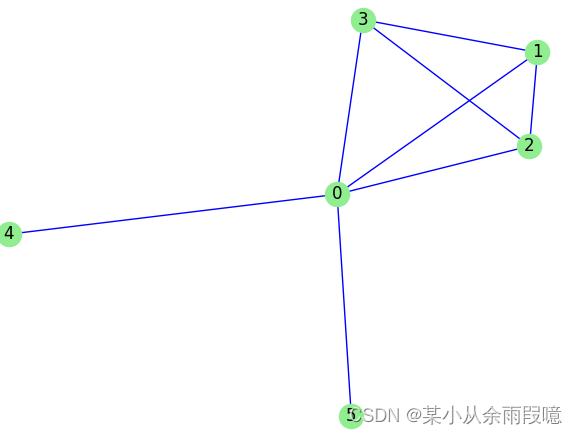
连通分量(Connected Component)
连通分量是指图中所有节点之间都有路径可以到达的最大子图。在无向图中,连通分量是图的一个重要性质,表示节点之间的连通性。在有向图中,有弱连通分量和强连通分量。弱连通分量是将有向图视为无向图后得到的连通分量,强连通分量则是指在有向图中,所有节点之间有路径可以到达的子图。
在NetworkX中,可以使用 connected_components() 方法找到无向图中的连通分量例如:
python"># 找到空手道俱乐部网络(无向图)中的连通分量
connected_components = list(nx.connected_components(G))
print("连通分量:", connected_components)
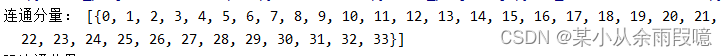
使用 strongly_connected_components() 和 weakly_connected_components() 方法找到有向图中的强连通和弱连通分量,例如:
python"># 创建一个有向图,让图中一些点不连接
# 找到有向图中的强连通分量DG = nx.DiGraph([(1, 2), (2, 3), (3, 1), (4, 5)])# 可视化图
nx.draw(DG, with_labels = True, node_color='Gold')
plt.show()strongly_connected_components = list(nx.strongly_connected_components(DG))
print("强连通分量:", strongly_connected_components)# 找到有向图中的弱连通分量
weakly_connected_components = list(nx.weakly_connected_components(DG))
print("弱连通分量:", weakly_connected_components)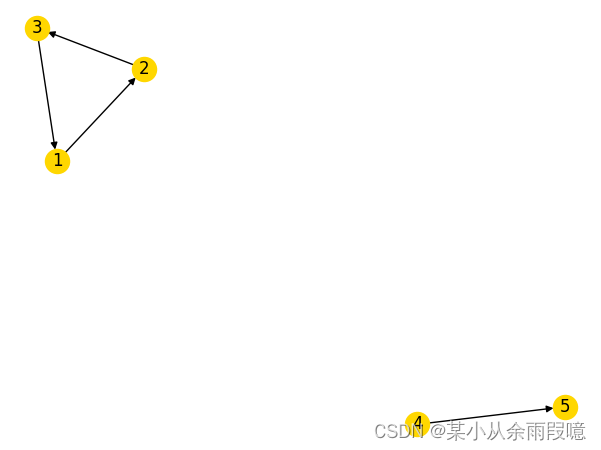

连通图(Connected Graph)
连通图是指一个无向图中,所有节点之间都存在至少一条路径。连通图只有一个连通分量。
在NetworkX中,可以使用 is_connected() 方法检查一个无向图是否是连通图。例如:
python"># 检查无向图是否是连通图
is_connected = nx.is_connected(G)
print("该图是否是连通图:", is_connected)3.6 聚类系数(Clustering Coefficient)

python"># 创建一个空手道俱乐部网络
G = nx.karate_club_graph()# 计算每个节点的局部聚类系数
local_clustering = nx.clustering(G)# 计算全局聚类系数(平均局部聚类系数)
global_clustering = nx.average_clustering(G)print("局部聚类系数:", local_clustering) # 打印所有节点的局部聚类系数
print("全局聚类系数:", global_clustering) # 打印全局聚类系数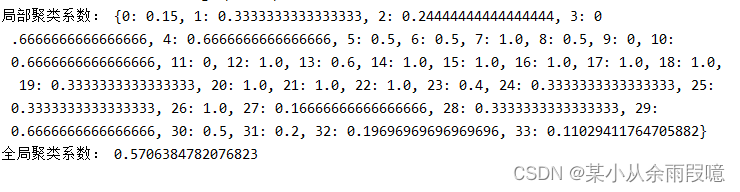
3.7 接近中心度 (closeness centrality)
接近中心度(Closeness Centrality)是一种度量图中节点的重要性或影响力的指标。它衡量了一个节点与其他所有节点之间的距离,也即最短路径的平均距离。接近中心度的值越高,意味着该节点与其他节点之间的距离越短,具有更大的影响力。
接近中心性计算:计算一个节点与其他节点之间的最短路径之和,再对得到的和求倒数,得到该节点的接近中心性得分。
更常见的做法是将该得分归一化,以此表示最短路径的平均长度,而不是最短路径之和。利用这一修正方法可以比较在不同规模的图中节点的接近中心性。

在NetworkX中,可以使用 closeness_centrality() 方法计算节点的接近中心度:
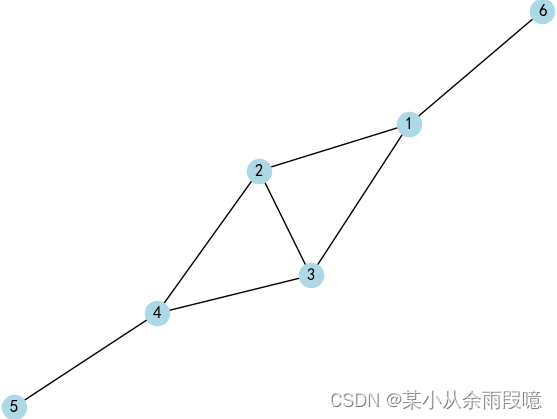
python"># 创建一个图
G= nx.Graph()# 添加节点和边
G.add_edges_from([(1, 2),(1, 3),(2, 3),(2, 4),(3, 4),(4,5)])# 计算接近中心度
closeness = nx.closeness_centrality(G)
# 将接近中心度转换为列表
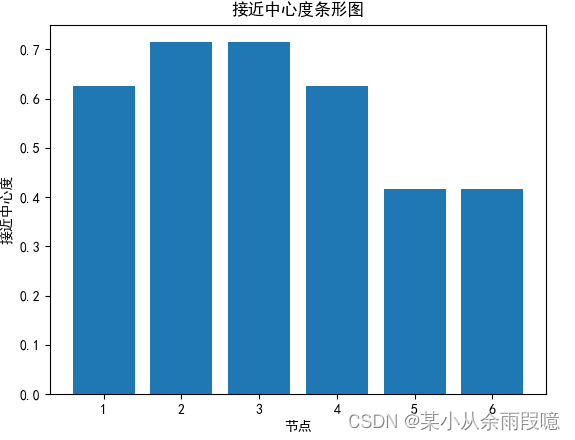
closeness_values =list(closeness.values())# 绘制条形
plt.bar(range(len(closeness_values)),closeness_values)
plt.xlabel("节点")
plt.ylabel("接近中心度")
plt.title("接近中心度条形图")# 标记节点
plt.xticks(range(len(closeness_values)),closeness.keys())
# 显示图形
plt.show()
4. 邻接矩阵、关联矩阵、拉普拉斯矩阵
4.1 邻接矩阵
邻接矩阵(Adjacency Matrix)是图的一种常用表示方式,它是一个方阵,用于表示图中的节点和边的关系。邻接矩阵的大小为 𝑛×𝑛,其中 𝑛 是图中的节点数量。
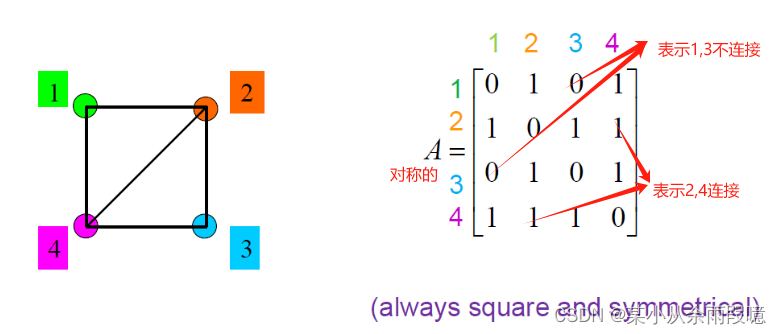
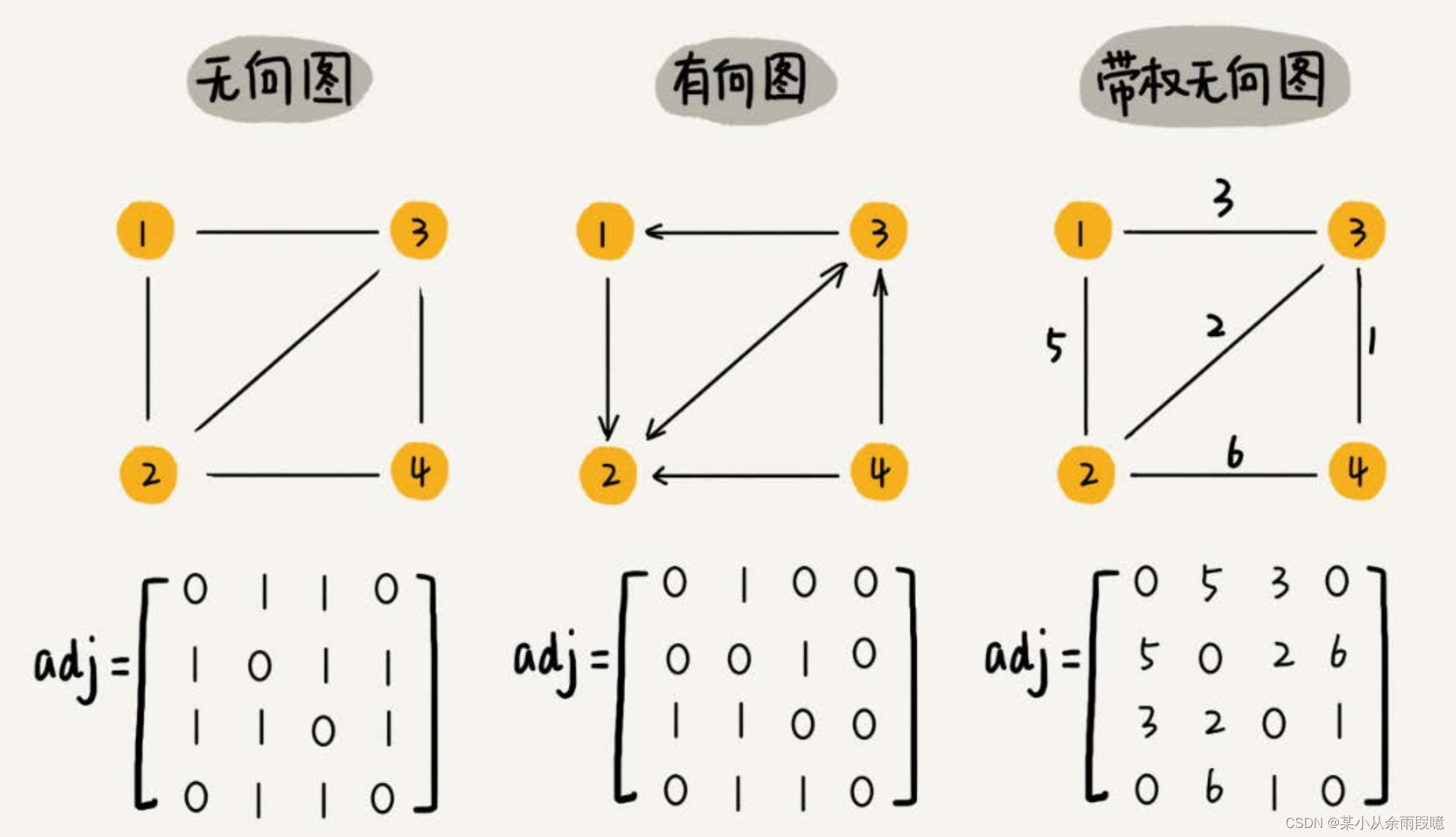
1.无向图的邻接矩阵
在无向图中,邻接矩阵是对称的。若节点 𝑖 和节点 𝑗 之间存在边,则矩阵的相应位置为 1,否则为 0。
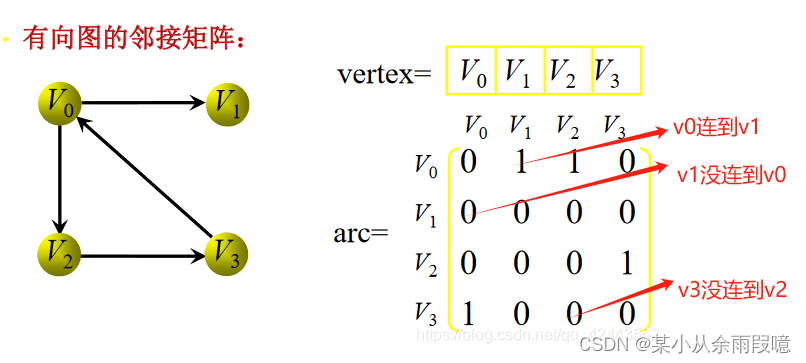
2.有向图的邻接矩阵
在有向图中,邻接矩阵不一定是对称的。若从节点 𝑖 到节点 𝑗 有边,则矩阵的位置 [𝑖,𝑗]为 1,否则为 0。
3.加权图的邻接矩阵
在加权图中,邻接矩阵的位置值是边的权重。如果没有边,则该位置的值可以设置为 0、无穷大或其他特殊值。
4.生成邻接矩阵
在NetworkX中,可以使用 to_numpy_array() 或 adjacency_matrix() 方法来生成图的邻接矩阵。
1.无向图的邻接矩阵:
python"># 创建一个图
G= nx.Graph()# 添加节点和边
G.add_edges_from([(1, 2),(1, 3),(2, 4),(3, 4),(4,5)])
nx.draw(G, with_labels = True, node_color='yellow')
plt.show()# 生成邻接矩阵
adj_matrix = nx.to_numpy_array(G)
print("无向图的邻接矩阵:\n", adj_matrix)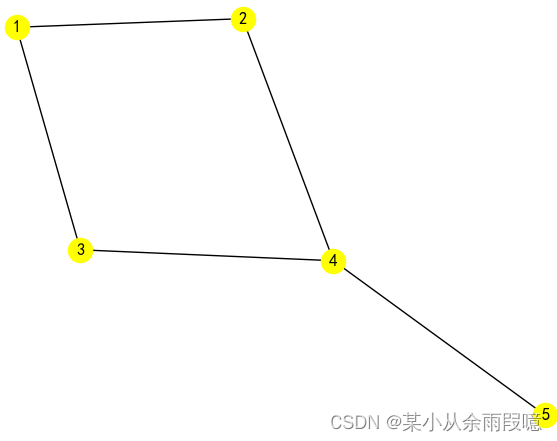

2.有向图的邻接矩阵
python"># 创建一个有向图
DG = nx.DiGraph([(1, 2), (2, 3), (3, 1), (4, 5)])
nx.draw(DG, with_labels = True, node_color='Lightblue')
plt.show()# 生成邻接矩阵
adj_matrix = nx.to_numpy_array(DG)
print("有向图的邻接矩阵:\n", adj_matrix) 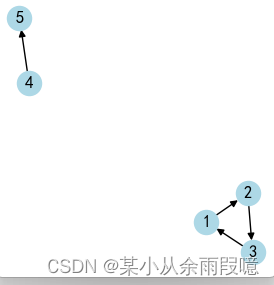

3.加权有向图的邻接矩阵:
python"># 创建一个空的加权图
WG = nx.DiGraph() # 也可以是 nx.Graph(),取决于是否需要有向# 添加节点
WG.add_nodes_from([1, 2, 3, 4])# 添加加权边
WG.add_edge(1, 2, weight=0.5)
WG.add_edge(2, 3, weight=1.2)
WG.add_edge(3, 4, weight=0.8)
WG.add_edge(4, 1, weight=0.5)# 绘制加权图
# 使用边权重进行可视化
edge_labels = nx.get_edge_attributes(WG, 'weight')nx.draw(WG, with_labels=True, node_color='lightgreen', arrowstyle='-|>')
nx.draw_networkx_edge_labels(WG, pos=nx.spring_layout(WG), edge_labels=edge_labels)
plt.show()# 生成加权邻接矩阵
adj_matrix = nx.to_numpy_array(WG, weight='weight')print("加权图的邻接矩阵:\n", adj_matrix)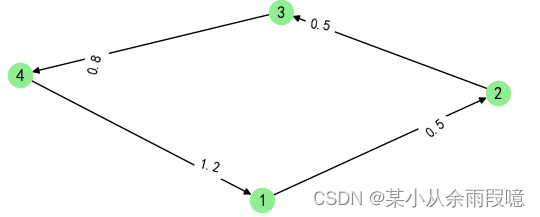

4.2 关联矩阵
关联矩阵(Incidence Matrix)是图的一种表示方式,展示了节点和边之间的关系。对于给定的图,关联矩阵是一个大小为 𝑛×𝑚n×m 的矩阵,其中 𝑛n 是节点的数量,𝑚m 是边的数量。
1.无向图的关联矩阵
在无向图中,关联矩阵的每一行对应一个节点,每一列对应一条边。如果某条边连接了节点 𝑖 和节点 𝑗,那么对应的列中这两个节点的行将设置为 1。
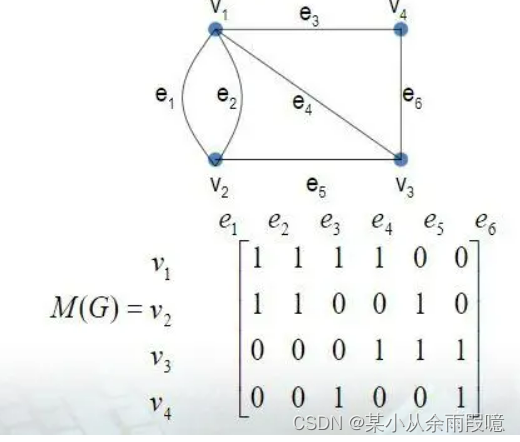
2.有向图的关联矩阵
在有向图中,关联矩阵不仅表示节点和边之间的关系,还表明边的方向。如果边从节点 𝑖 指向节点 𝑗,那么对应的列在节点 𝑖 的行中设置为 -1,而在节点 𝑗 的行中设置为 1。
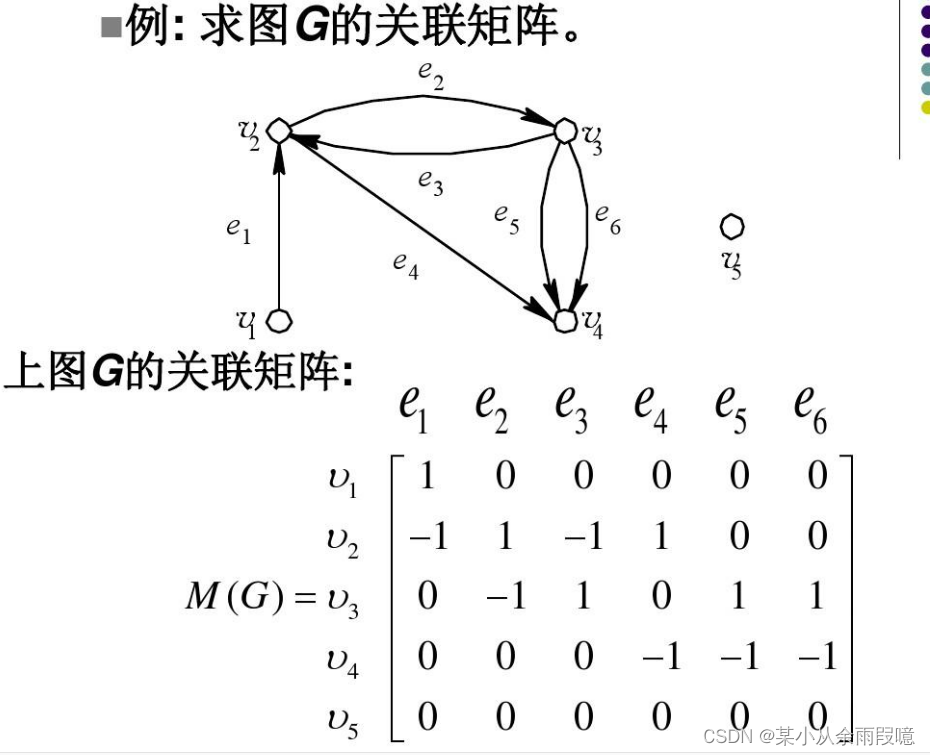
3.生成关联矩阵
在NetworkX中,您可以使用 incidence_matrix() 方法生成关联矩阵。
python"># 创建一个有向图
DG = nx.DiGraph([(1, 2), (2, 3), (3, 1), (4, 5)])
nx.draw(DG, with_labels = True, node_color='Lightblue')
plt.show()# 生成关联矩阵
inc_matrix = nx.incidence_matrix(DG, oriented=True).toarray()
print("有向图的关联矩阵:\n", inc_matrix)

python"># 创建一个空的加权图
WG = nx.DiGraph() # 也可以是 nx.Graph(),取决于是否需要有向# 添加节点
WG.add_nodes_from([1, 2, 3, 4])# 添加加权边
WG.add_edge(1, 2, weight=0.5)
WG.add_edge(2, 3, weight=1.2)
WG.add_edge(3, 4, weight=0.8)
WG.add_edge(4, 1, weight=0.5)
WG.add_edge(2, 4, weight=0.1)# 绘制加权图
# 使用边权重进行可视化
edge_labels = nx.get_edge_attributes(WG, 'weight')nx.draw(WG, with_labels=True, node_color='lightgreen', arrowstyle='-|>')
nx.draw_networkx_edge_labels(WG, pos=nx.spring_layout(WG), edge_labels=edge_labels)
plt.show()# 生成加权关联矩矩阵
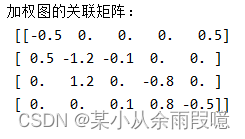
inc_matrix = nx.incidence_matrix(WG, oriented=True, weight='weight').toarray()
print("加权图的关联矩阵:\n", inc_matrix)
4.3 拉普拉斯矩阵
拉普拉斯矩阵(Laplacian Matrix)是基于图的度矩阵和邻接矩阵定义的。设 𝐷 为度矩阵,是一个对角矩阵,其中每个对角线元素表示相应节点的度;设 𝐴 为邻接矩阵,表示图中节点之间的连接关系。
拉普拉斯矩阵定义为: 𝐿=𝐷−𝐴
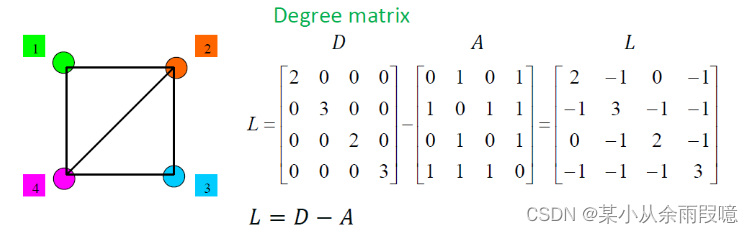
拉普拉斯矩阵的性质:
- 拉普拉斯矩阵是对称矩阵。
- 对于无向图,拉普拉斯矩阵的每一行和每一列的和都是零。
- 拉普拉斯矩阵的特征值可以反映图的性质,例如第二小的特征值(通常称为 Fiedler 值)与图的连通性相关。
生成拉普拉斯矩阵
在NetworkX中,可以使用 laplacian_matrix() 或 normalized_laplacian_matrix() 方法生成拉普拉斯矩阵。
5. 图的类型
- 按照不同的划分规则,图可以被划分为很多不同的种类。在 2.2 节中,我们根据边是否具有指向性,区分得到了有向图和无向图。下面,我们会根据更多不同的属性来对图进行划分。
5.1 图的拓扑结构
图的拓扑结构是指图中节点和边的组织方式,以及它们之间的连接关系。拓扑结构反映了图的整体布局和性质,揭示了图的某些特征和行为。
例如,环(Cycle):节点和边形成的闭合路径。 树(Tree):无环连通无向图。 森林(Forest):不连通的树的集合等。
根据图的拓扑结构,规则网络(regular network)可以分为
- 全连接网络(fully-connected network)(下图左)
- 环形网络(ring-shape network)(下图中)
- 星形网络(start-shape network)(下图右)
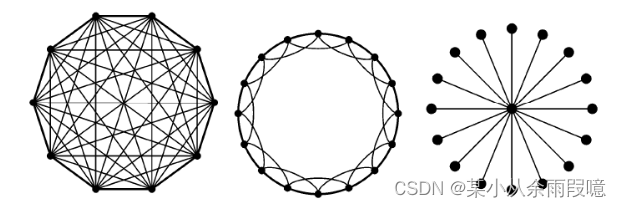
图的拓扑结构在分析网络、社交关系、数据流、任务依赖等方面具有重要意义。理解图的拓扑结构可以帮助我们理解系统的行为和特征。
5.2 同质图和异质图
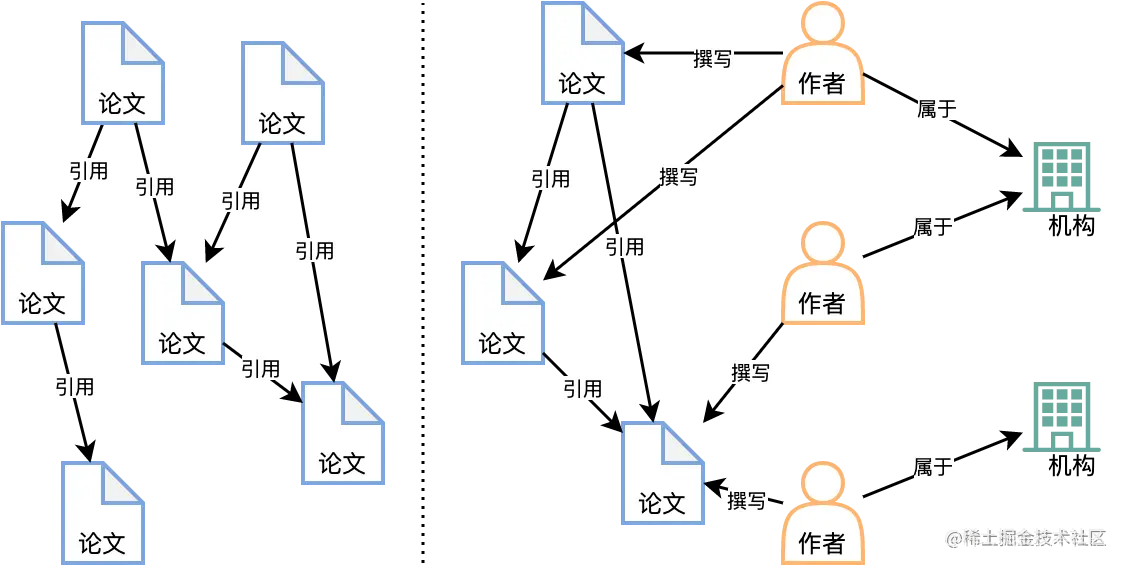
质图(Homogeneous Graph)和异质图(Heterogeneous Graph)是根据图中节点和边的性质分类的两种概念。这两个概念主要用来区分网络中节点和边的同质性或异质性。
- 同质图(Homogeneous Graph):只有一种类型的节点和一种类型的边的图。
- 异质图(Heterogeneous Graph):存在多种类型的节点和多种类型的边的图。
5.3 二分图
二分图是一类特殊的图,又称为二部图、偶图、双分图。二分图的顶点可以分成两个互斥的独立集合 U 和 V 的图,使得所有边都是连结一个 U 中的点和一个 V 中的点。
也就是,节点分为两类,只有不同类的节点之间存在边。

二分图在很多实际应用中都发挥着重要作用,包括:
- 匹配问题:如婚配问题、工作分配问题。
- 社交网络:表示两类不同节点的关系,例如用户和兴趣、学生和课程。
- 生物信息学:表示蛋白质与基因、药物与靶标的关系。
创建二分图:
python"># 创建一个二分图
B = nx.Graph()# 添加左组节点
B.add_nodes_from([1, 2, 3, 4], bipartite=0) # bipartite=0 表示左组
# 添加右组节点
B.add_nodes_from(['A', 'B', 'C', 'D'], bipartite=1) # bipartite=1 表示右组# 添加边,连接左右组
B.add_edges_from([(1, 'A'), (1, 'C'), (2, 'C'), (3, 'D'), (3, 'C'), (1, 'B'), (4, 'D')])# 检查是否是二分图
is_bipartite = nx.is_bipartite(B)# 确定布局
# data=True: bipartite为 1
left_nodes = {n for n, d in B.nodes(data=True) if d["bipartite"] == 0}
pos = nx.bipartite_layout(B, left_nodes)# 设置颜色
node_colors = ['lightblue' if node in left_nodes else 'lightgreen' for node in B.nodes()]# 可视化二分图
plt.figure(figsize=(8, 6))
nx.draw(B, pos, with_labels=True, node_color=node_colors, edge_color='gray')
plt.title("二分图的可视化")
plt.show() # 显示图形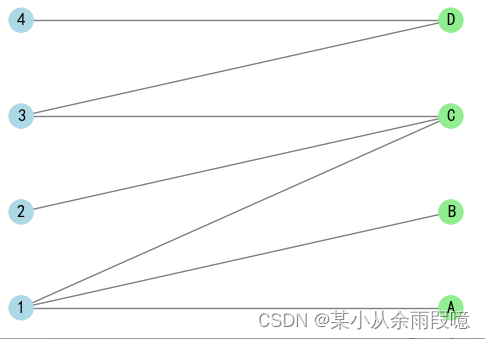
在分配问题中,我们通常有两个节点组:一个是资源或任务的提供者,另一个是需求者或接收者。二分图的特性使其非常适合表示这些分配问题。分配问题的目标通常是将左组和右组的节点进行最佳匹配,以满足某种条件或优化某个目标。在实际应用中,分配问题经常涉及优化,例如:
- 最大化匹配:找到在二分图中将两个组连接最多的匹配方式。
- 最小成本匹配:找到一种匹配方式,使总成本最小化(每条边有权重表示成本)。
- 任务-人员分配:在一个组织中,将任务有效分配给合适的人员。
解决分配问题的常用算法包括:
- 匈牙利算法:一种用于求解最大匹配和最小成本匹配的有效算法。
- Hopcroft-Karp算法:用于求解二分图最大匹配的高效算法。
eg. 匈牙利法求解指派问题(运筹学):