目录
Querying a Graph in Python
Querying a Graph in Python
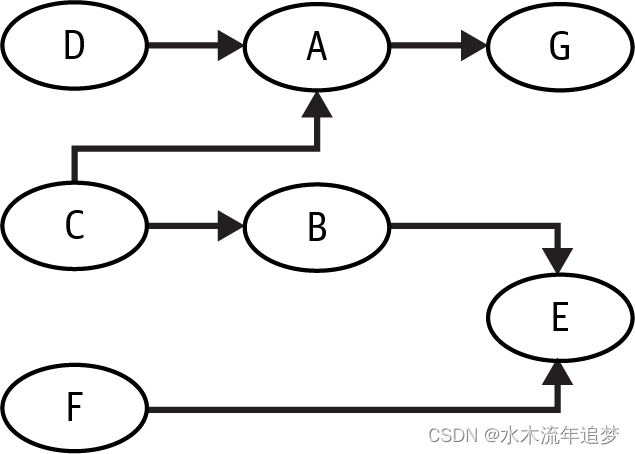
在接下来的时刻,你将把这个图输入到一个Python库中,这将使得回答关于它的问题变得相当容易。但在你这样做之前,作为一项练习,为了更好地理解你刚刚学到的概念,试着独立回答以下问题:
- D和C是否相互依赖?
- 在给定A的情况下,D和C是否相互依赖?
- 在给定G的情况下,D和C是否相互依赖?
- A和B是否相互依赖?
- 在给定C的情况下,A和B是否相互依赖?
- G和F是否相互依赖?
- 在给定E的情况下,G和F是否相互依赖?
现在,为了验证你的答案是否正确,你可以将这个图输入到networkx中的DiGraph。networkx是一个处理图形模型的库,它包含了许多有用算法,可以帮助你检查这个图
python"> import networkx as nxmodel = nx.DiGraph([("C", "A"),("C", "B"),("D", "A"),("B", "E"),("F", "E"),("A", "G"),])作为开始,让我们以D和C为例。它们构成了你之前看到的不道德结构(immorality structure),其中A是碰撞点(collider)。根据在不道德结构中关于独立性的规则,你知道D和C是独立的。你也知道,如果你在碰撞点A上进行条件化,那么它们之间开始产生关联。d_separated 方法可以告诉你在图中两个变量间是否存在关联流动(d-分离是表达图中两个变量间独立性的另一种方式)。为了对某个变量进行条件化,你可以将其添加到观察集合中。例如,为了检查在给定A的情况下D和C是否相关,你可以使用 d_separated 并传递第四个参数 z={"A"}。
python"> print("Are D and C dependent?")print(not(nx.d_separated(model, {"D"}, {"C"}, {})))print("Are D and C dependent given A?")print(not(nx.d_separated(model, {"D"}, {"C"}, {"A"})))print("Are D and C dependent given G?")print(not(nx.d_separated(model, {"D"}, {"C"}, {"G"})))Are D and C dependent?FalseAre D and C dependent given A?TrueAre D and C dependent given G?True接下来,注意D、A和G形成了一个链式结构。你知道在链式结构中关联会流动,因此D与G并非独立。然而,如果你在中间变量A上进行条件化,你就会阻断关联的流动:
python"> print("Are G and D dependent?")print(not(nx.d_separated(model, {"G"}, {"D"}, {})))print("Are G and D dependent given A?")print(not(nx.d_separated(model, {"G"}, {"D"}, {"A"})))Are G and D dependent?TrueAre G and D dependent given A?False最后一个需要回顾的结构是叉状结构。可以看到A、B和C形成了一个叉状结构,其中C是A和B的共同原因。你知道关联会通过叉状结构流动,因此A和B不是独立的。但是,如果你在共同原因上进行条件化,关联的路径就被阻断了:
python"> print("Are A and B dependent?")print(not(nx.d_separated(model, {"A"}, {"B"}, {})))print("Are A and B dependent given C?")print(not(nx.d_separated(model, {"A"}, {"B"}, {"C"})))Are A and B dependent?TrueAre A and B dependent given C?False最后,让我们将所有内容结合起来,讨论G和F。两者之间是否有关联流动?我们从G开始。你知道因为G和E处于叉状结构中,所以两者间存在关联。然而,关联会在碰撞点E处停止,这意味着G和F是独立的。但如果在E上进行条件化,关联就开始通过碰撞点流动,路径被打开,连接了G和F:
python"> print("Are G and F dependent?")print(not(nx.d_separated(model, {"G"}, {"F"}, {})))print("Are G and F dependent given E?")print(not(nx.d_separated(model, {"G"}, {"F"}, {"E"})))Are G and F dependent?FalseAre G and F dependent given E?True这真是太好了。你不仅学到了图中三种基本结构,还看到了如何使用现成的算法来检查图中的独立性。但这与因果推断有什么关系呢?现在是时候回到开头探讨的问题了。回想一下,我们试图理解聘请昂贵的一流顾问对公司业绩的影响,我们用以下图来描绘这个问题:
你可以利用新学到的技能来看为什么在这个图中关联并不等同于因果。注意到在这个图中有一个叉状结构。因此,在顾问和公司未来业绩之间存在两种关联流动:一条直接的因果路径和一条由共同原因混淆的非因果路径。后者被称为后门路径。在这个图中后门路径的存在表明,观察到的顾问与公司业绩之间的关联不能仅仅归因于因果关系。
理解关联如何通过非因果路径在图中流动,将使你在谈论关联与因果的区别时更加精确。出于这个原因,重新审视识别概念,现在在图形模型的新视角下,将是值得的。