前言
延续前面所讲的一维前缀和以及差分,现在来写写二维前缀和与差分
主要这个画图就比前面的一维前缀和与差分复杂一点,不过大体思路是一样的
一维和二维的主要思路在于一维是只针对对一行一列,而二维是针对与一个矩阵的
好吧,开始讲解
二维前缀和
问题描述
有一个二维数组,int arr[i][j]中从{x1,y1}->{x2,y2}的范围内求和
这里的范围是一个矩形而不是一个路径
举例 ,比如 下面对于一个三行五列的二维数组 求{1,1}->{2,2}的和就是求红色部分的和
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
暴力思路
那就是根据下表依次相加复杂度为o((x2-x1)*(y2-y1))
其实就是行乘列,这里的暴力代码实在是太简单了,但是不能太懒,还是给大家敲
#define col 5
#define line 3
int main()
{int arr[line][col] = {{1,2,3,4,5},{6,7,8,9,10},{11,12,13,14,15}};printf("请输入4个数表示两个坐标\n");int x1, y1, x2, y2;int sum = 0;scanf("%d %d %d %d", &x1,&y1,&x2,&y2);for (int i = x1; i<= x2; i++)for (int j = y1; j<= y2; j++)sum += arr[i][j];printf("%d", sum);return 0;
}这里的时间复杂度是平方级别的
二维前缀和的思路
1.二维前缀数组的构建
这玩意用文字讲,费时间呢,还是画图来讲解吧
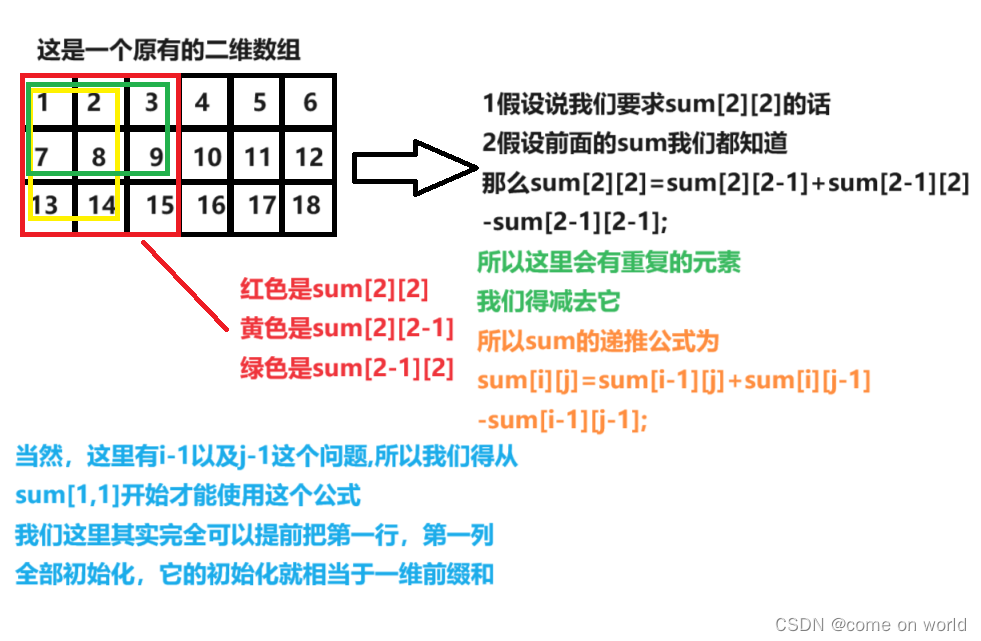
我们这里先把它的代码给出
void pre_sum(int arr[][col])
{sum[0][0] = arr[0][0];for (int i = 1; i < col; i++)sum[0][i] = sum[0][i - 1] + arr[0][i];for (int j = 1; j < line;j++)sum[j][0] = sum[j - 1][0] + arr[j][0];for (int i = 1; i < line; i++){for (int j = 1; j < col; j++){sum[i][j] = sum[i][j - 1] + sum[i - 1][j] - sum[i - 1][j - 1]+arr[i][j];}}
}2前缀和数组的使用
还是看图吧
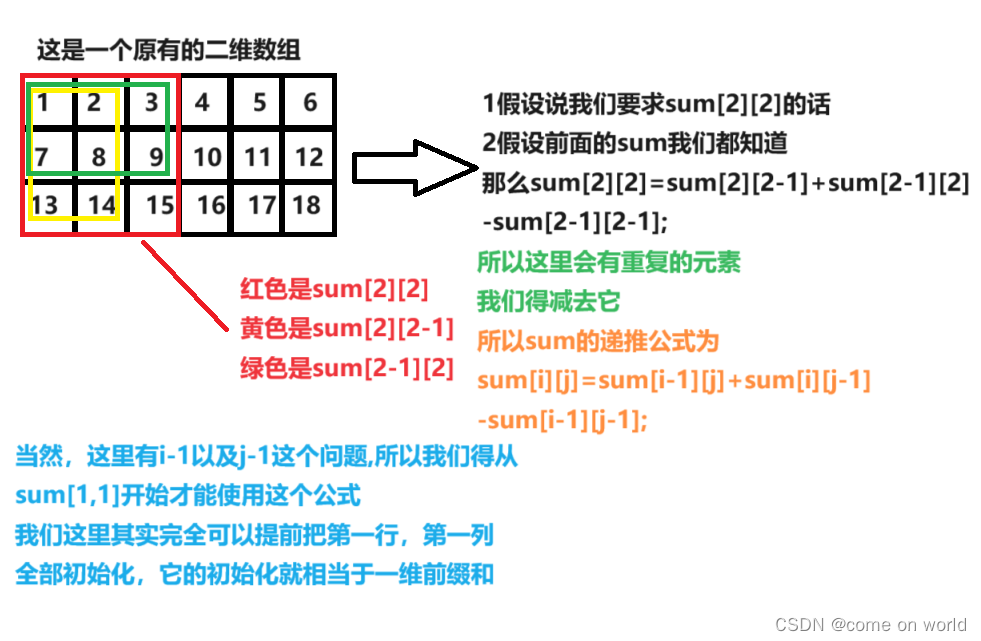
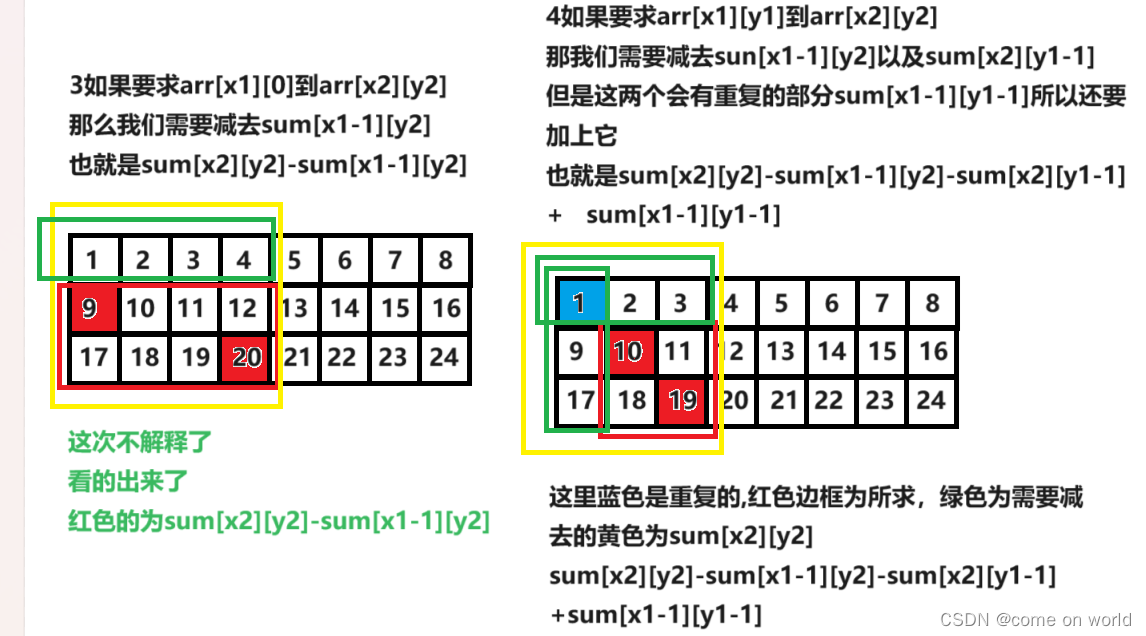
OK
我们来看代码吧
//二维前缀和
#define line 3
#define col 5
int sum[line][col];
void pre_sum(int arr[][col])
{sum[0][0] = arr[0][0];for (int i = 1; i < col; i++)sum[0][i] = sum[0][i - 1] + arr[0][i];for (int j = 1; j < line;j++)sum[j][0] = sum[j - 1][0] + arr[j][0];for (int i = 1; i < line; i++){for (int j = 1; j < col; j++){sum[i][j] = sum[i][j - 1] + sum[i - 1][j] - sum[i - 1][j - 1]+arr[i][j];}}
}
int result(int x1, int y1, int x2, int y2)
{if (x1 == 0 && y1 == 0)return sum[x2][y2];else if (x1 == 0)return sum[x2][y2] - sum[x2][y1 - 1];else if (y1 == 0)return sum[x2][y2] - sum[x1 - 1][y2];else return sum[x2][y2] - sum[x2][y1-1] - sum[x1-1][y2] + sum[x1 - 1][y1 - 1];
}
int main()
{int arr[line][col] = {{1, 2, 3, 4, 5},{6, 7, 8, 9, 10},{11,12,13,14,15}};pre_sum(arr);printf("%d", result(1, 0, 2, 2));
}那么接下来看差分了
二维差分
理解了二为前缀和,那么二维差分就很简单了,同样也是一个矩阵作为作用的对象
问题描述
有一个二维数组,int arr[i][j]中从{x1,y1}->{x2,y2}的范围内求和
这里的范围是一个矩形而不是一个路径
举例 ,比如 下面对于一个三行五列的二维数组 求{1,1}->{2,2}对他们加上某个数
假设这个数为1
1 1 1 1 1 那么结果是 1 1 1 1 1
1 1 1 1 1 1 2 2 1 1
1 1 1 1 1 1 2 2 1 1
暴力思路
其实真的有点不想写了,哎呦!!!!!!
还是再来吧!!!!!!
看代码
#define col 5
#define line 3
int main()
{int arr[line][col] = {{1,2,3,4,5},{6,7,8,9,10},{11,12,13,14,15}};printf("请输入4个数表示两个坐标\n");int x1, y1, x2, y2,val;scanf("%d %d %d %d", &x1,&y1,&x2,&y2);printf("再输入一个数作为操作数");scanf("%d",&val);for (int i = x1; i<= x2; i++)for (int j = y1; j<= y2; j++)arr[i][j]+=val;printf("%d", sum);return 0;
}差分思路
其实这里用不到差分数组,只是把一个比原来二维数组行列都大1的一个数组全部初始化为0
然后,作为一个影响,去进行前缀和,把产生的影响加到原有的数组中
看图吧
思路上与前缀和差不多,我们主要讲如何使用
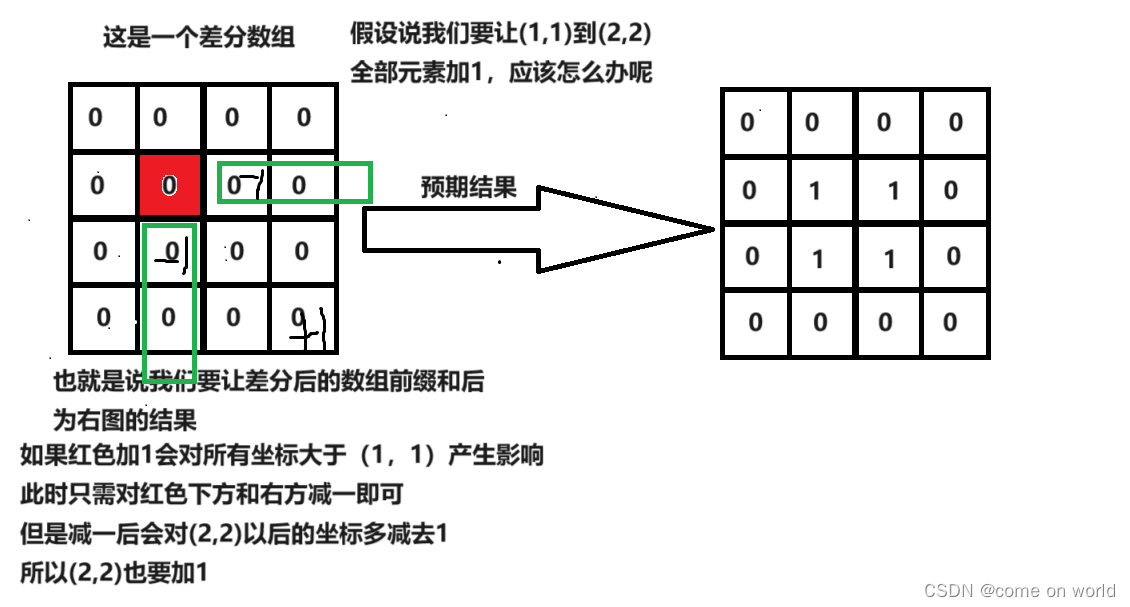
假设有两个坐标(x1,y1),(x2,y2)
构建一个二维数组,元素全部为0 d[line+1][col+1];
其实核心的代码为
d[x1][y1] += value;产生影响
d[x2 + 1][y1] -= value;让后面的元素不受影响
d[x1][y2 + 1] -= value;让后面的元素不受影响
d[x2 + 1][y2 + 1] += value;让后面的元素不受影响,多减去了
看图
看代码呗
#define line 3
#define col 5
int d[line + 1][col + 1] = {0};
void pre_d(int arr[][col])
{for (int i = 1; i <=col; i++)d[0][i]+=d[0][i-1];for (int j = 1; j <=line;j++)d[j][0]+=d[j-1][0];for (int i = 1; i <=line; i++){for (int j = 1; j <=col; j++){d[i][j]+=d[i][j-1]+d[i-1][j]-d[i-1][j-1];}}for (int i = 0; i < line; i++){for (int j = 0; j < col; j++){arr[i][j] += d[i][j];}}
}
void fun(int x1, int y1, int x2, int y2,int value)
{d[x1][y1] += value;d[x2 + 1][y1] -= value;d[x1][y2 + 1] -= value;d[x2 + 1][y2 + 1] += value;
}
void printf_a(int arr[][col])
{for (int i =0; i < line; i++){for (int j = 0; j < col; j++)printf("%d ", arr[i][j]);printf("\n");}
}
void printf_d()
{for (int i = 0; i <=line; i++){for (int j = 0; j<=col;j++)printf("%d ", d[i][j]);printf("\n");}
}
int main()
{int arr[line][col] = {{1, 2, 3, 4, 5},{6, 7, 8, 9, 10},{11,12,13,14,15}};fun(0, 0, 2, 1,-1);fun(0, 2, 2, 4, 5);pre_d(arr);printf("\n");printf_a(arr);
}
总结
最后,如果大家感兴趣的话可以试试三维数组
好吧,就这样吧,睡个好觉,祝大家开心啊!