1.ArrayList的缺陷
ArraryList由于底层是一段连续的空间,所以在ArrayList任意位置插入或者删除元素时,就 需要将后续元素往前或者往后搬移,时间复杂度为O(n),效率比较低,因此ArrayList不适合做任意位置插入和删除比较多的场景。因此,Java集合中还引入了LinkedList,即链表结构。
2.链表的概念和结构
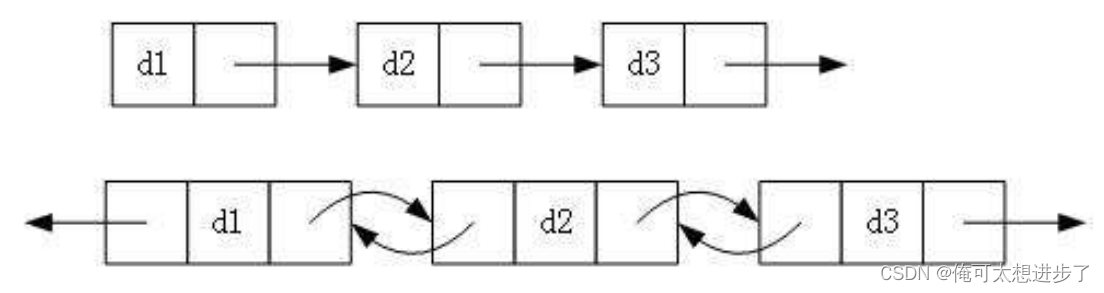
链表是一种物理结构上非连续的存储结构,数据元素的逻辑顺序是通过链表中的引用链接次序实现 的。我们先来看张图:

注意:
- 从上图可以看出,链式结构在逻辑上是连续的,但是物理上不一定连续
- 现实中的结点一般都是从堆上申请出来的
- 从堆上申请的空间,是按照一定的策略来分配的,两次申请的空间可能连续,也可能不连续
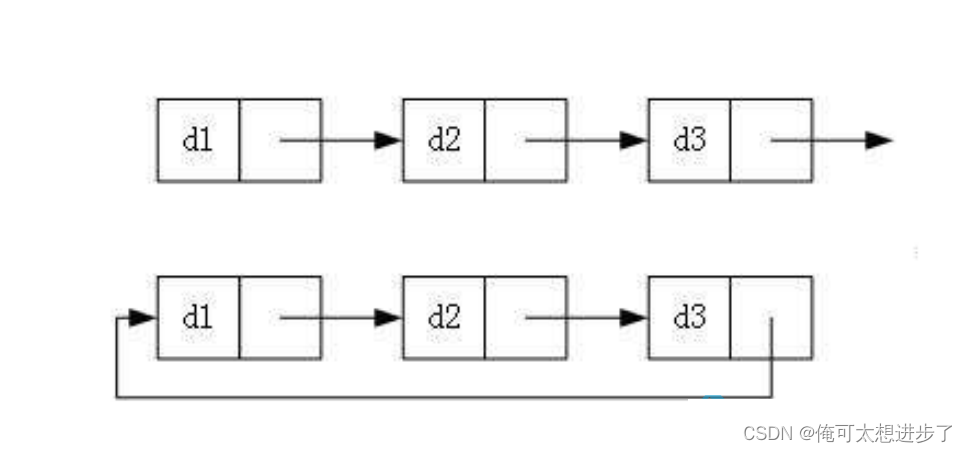
在实际情况中,链表的结构非常多样,以下情况组合起来就有八种链表结构:
1.单向或者双向
2.带头或者不带头

3.循环或者非循环
尽管链表的结构有这么多,但重要的有两种:
3.LinkedList
LinkedList 是一种常见的数据结构,它表示一个节点的集合,这些节点不仅保存了数据,还保存了指向下一个节点的引用。这种结构允许我们从头尾两个方向遍历数据,同时也可以在任意位置插入或删除节点。
LinkedList 的主要特点包括:
- 动态大小:
LinkedList的大小可以在运行时动态改变,可以方便地添加或删除元素。 - 有序性:元素在
LinkedList中是按照它们被插入的顺序排列的。 - 插入和删除的高效性:在
LinkedList的任何位置插入或删除元素的时间复杂度都是 O(1),因为只需要修改相邻节点的引用即可。但是,请注意,找到要插入或删除的位置的时间复杂度可能依赖于具体的实现和搜索策略。 - 空间开销:由于每个节点除了保存数据外,还需要保存指向下一个节点的引用,因此
LinkedList通常比数组或固定大小的列表占用更多的空间。 - 不支持随机访问:与数组不同,链表不支持快速随机访问元素,因为需要从头节点或尾节点开始逐个遍历才能找到目标元素。
LinkedList 的实现可以有多种形式,但最常见的两种是单向链表(每个节点只有一个指向下一个节点的引用)和双向链表(每个节点都有一个指向前一个节点和一个指向下一个节点的引用)。双向链表提供了更强大的功能,比如可以从尾部开始遍历,或者在任意位置向前或向后移动。
在集合框架中,LinkedList也实现了List接口,具体如下: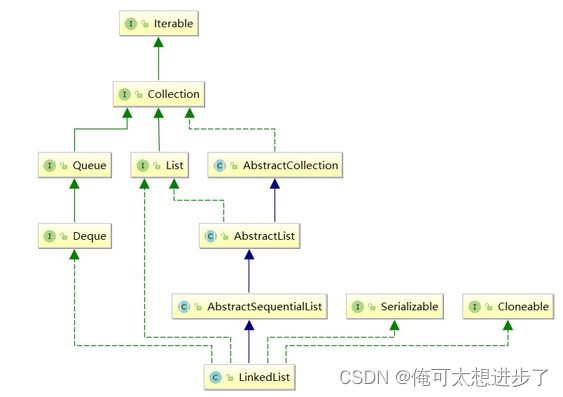
同样地我们能从上图得出一些结论:
- LinkedList实现了List接口
- LinkedList底层使用了双向链表
- LinkedList没有实现RandomAccess接口,因此LinkedList不支持随机访问
- LinkedList的任意位置插入删除元素时效率比较高,时间复杂度为O(1)
- LinkedList比较适合任意位置插入的场景
4.关于使用
4.1LinkedList的构造
| 方法 | 解释 |
| LinkedList() | 无参构造 |
| public LinkedList(Collection<? extends E> c) | 使用其他集合容器中元素构造List |
示例
public static void main(String[] args) {//构造一个空的LinkedListList<Integer> list1=new LinkedList<>();List<String> List2=new ArrayList<>();list2.add("唱");list2.add("跳");list2.add("rap");list2.add("篮球");//使用ArrayList构造LinkeListList<String> list3 =new LinkeList<>(list2);
}4.2LinkedList的一些常用的方法介绍
| 方法 | 解释 |
| boolean add(E e) | 尾插 |
| void add(int index,E element) | 将e插入到index位置 |
| boolean addAll(Collection<? extends E> c) | 尾插c中的元素 |
| E remove(int index) | 删除index位置元素 |
| boolean remove(Object o) | 删除遇到的第一个o |
| E get(int index) | 获取下标index位置元素 |
| E set(int index,E element) | 将下标index位置元素设置为element |
| void clear() | 清空 |
| boolean contains(Object o) | 判断o是否在线性表中 |
| int indexOf(Object o) | 返回第一个o所在下标 |
| int lastIndexOf(Object o) | 返回最后一个o的下标 |
| List<E> sublist(int fromIndex,int toIndex) | 截取部分list |
4.3LinkedList的遍历
public static void main(String[] args) {LinkedList<Integer> list = new LinkedList<>();list.add(1); // add(elem): 表示尾插list.add(2);list.add(3);list.add(4);list.add(5);list.add(6);list.add(7);System.out.println(list.size());// foreach遍历for (int e:list) {System.out.print(e + " ");}System.out.println();// 使用迭代器遍历---正向遍历ListIterator<Integer> it = list.listIterator();while(it.hasNext()){System.out.print(it.next()+ " ");}System.out.println();// 使用反向迭代器---反向遍历ListIterator<Integer> rit = list.listIterator(list.size());while (rit.hasPrevious()){System.out.print(rit.previous() +" ");}System.out.println();
}5.ArrayList和LinkedList
| 不同点 | ArrayList | LinkedList |
| 存储空间上 | 物理上一定连续 | 逻辑上连续,但物理上不一定连续 |
| 随机访问 | 支持O(1) | 不支持O(N) |
| 头插 | 需要搬移元素,效率低O(N) | 只需要修改引用的指向,时间复杂度为O(1) |
| 插入 | 空间不够时需要扩容 | 没有容量的概念 |
| 应用场景 | 元素高效存储+频繁访问 | 任意位置插入和删除频繁 |
![CodeForce[1500-2000]——1950F - 0, 1, 2, Tree!](https://img-blog.csdnimg.cn/direct/2a72ae2d7e7e44b88ac152c157ffe6bc.png)