这篇文章我们来介绍一下选择排序
目录
1.介绍
2.代码实现
3.小结与思考
1.介绍
选择排序:选择排序( Selection sort)是一种简单直观的排序算法。它的工作原理是每一趟从待排序的数据元素中选出最小(或最大)的一个元素,顺序放在已排好序的数列的最后,直到全部待排序的数据元素排完。
选择排序算法通过选择和交换来实现排序,其排序流程如下:
- 首先从原始数组中选择最小的1个数据,将其和位于第1个位置的数据交换。
- 接着从剩下的n-1个数据中选择次小的1个元素,将其和第2个位置的数据交换
- 然后,这样不断重复,直到最后两个数据完成交换。最后,便完成了对原始数组的从小到大的排序。
假如给定初始数据:(118,101,105,127,112)
一次排序:101,118,105,127,112
二次排序:101,105,118,127,112
三次排序:101,105,112,127,118
四次排序:101,105,112,118,127
(绿色为交换的数据)
每一趟在 n - i + 1 ( i=1, 2, ..., n-1 ) 个记录中选取关键字最小的记录作为有序序列中第 i 个记录。具体来说,假设长度为 n 的数组 arr,要按照从小到大排序,那么先从 n 个数字中找到最小值min1,如果最小值min1 的位置不在数组的最左端(也就是min1不等于arr[0]),则将最小值 min1 和 arr[0] 交换,接着在剩下的 n-1 个数字中找到最小值 min2,如果最小值 min2 不等于 arr[1],则交换这两个数字,依次类推,直到数组 arr 有序排列。算法的时间复杂度为 O(n^2)。
2.代码实现
下面看一下代码实现:
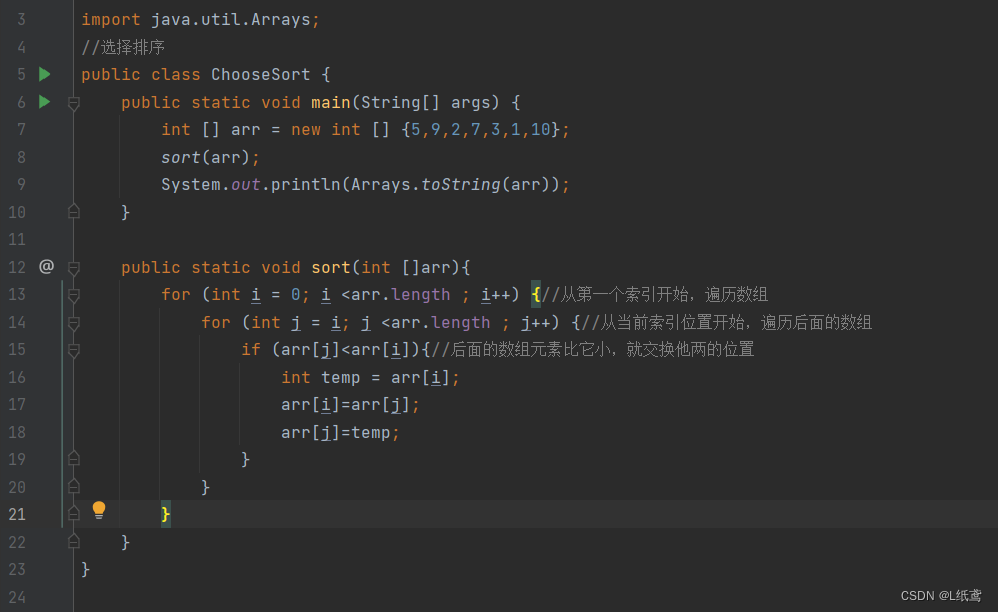
import java.util.Arrays;
//选择排序
public class ChooseSort {public static void main(String[] args) {int [] arr = new int [] {5,9,2,7,3,1,10};sort(arr);System.out.println(Arrays.toString(arr));}public static void sort(int []arr){for (int i = 0; i <arr.length ; i++) {//从第一个索引开始,遍历数组for (int j = i; j <arr.length ; j++) {//从当前索引位置开始,遍历后面的数组if (arr[j]<arr[i]){//后面的数组元素比它小,就交换他两的位置int temp = arr[i];arr[i]=arr[j];arr[j]=temp;}}}}
}
3.小结与思考
选择排序的思路还是很简单的。
就是给你一个无序数组,首先你要在里面找一个最大的,我们就假设最后一个是最大的,用一个变量 i 来记录它的位置,然后遍历这个数组,从头遍历,遍历的变量记为 j ,在遍历过程中,遇到 j 位置的数据比 i 位置的数据大的数值了,那么就交换 i 与 j 位置的数据,始终保持 i 位置的数据是最大的。第一轮遍历完成后,我们最大的数据就放到数组的末尾了,然后 i 的位置往前面移动,然后继续上面的流程。总体来说很简单。
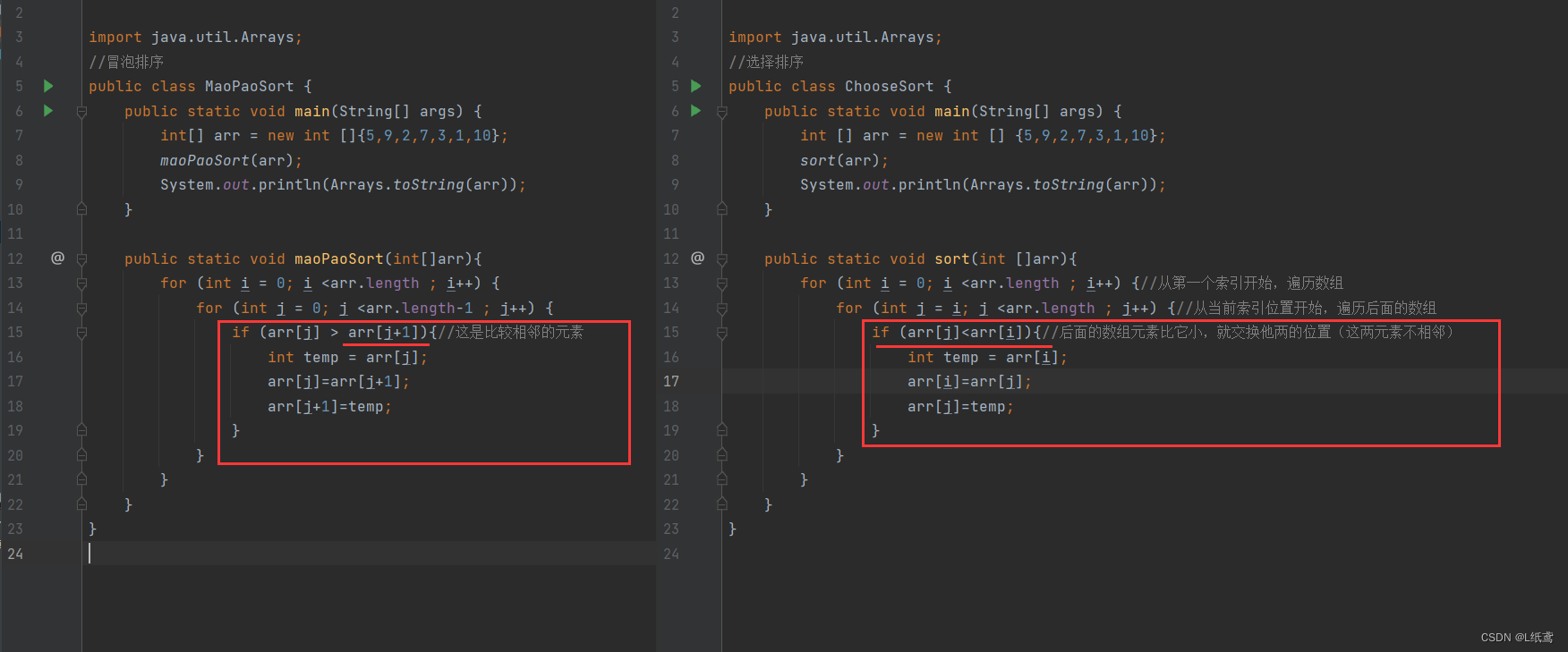
我一开始看这个选择排序时,把这个和冒泡排序弄混了,心想这个和冒泡排序的核心思路不都是一样的嘛,不都是双重遍历,然后交换嘛。但是看了冒泡排序代码后,发现二者还是有很大区别的。
冒泡排序的双重遍历中关键在第二重遍历,它是让相邻的两个进行比较然后交换。而选择排序是一开始假定一个最大的,然后和整个数组中元素依次比较然后交换,这就是二者的本质区别。
下面还是来看一下二者的代码吧: