【Python实战因果推断】3_因果效应异质性3

Effect by Model Quantile

Cumulative Effect

Effect by Model Quantile

制作 CATE 模型的想法源于发现哪些单元对治疗更敏感的必要性，目的是更有效地分配治疗。这种想法源于对个性化的渴望。如果这是我们的目标，那么如果能以某种方式将单元从更敏感到不太敏感排序，将会非常有用。既然您已经有了预测的 CATE，那么您就可以根据预测结果对治疗单元进行排序，并希望它也能根据真实的 CATE 对治疗单元进行排序。遗憾的是，您无法在单位层面对这种排序进行评估。但是，如果不需要呢？如果您评估的是由排序定义的组，又会怎样呢？

首先，请记住，如果治疗是随机分配的，您就不必担心混杂偏倚。估计一组单位的效果很容易。您所需要做的就是比较接受治疗和未接受治疗的结果。或者，更一般地说，在该组内对 Y 对 T 进行简单回归： $y_i=\beta_0+\beta_1t_i+e_i|X=x$ .

从简单线性回归的理论中，我们可以知道这一点： $\widehat{\beta_1}=\frac{\Sigma\left(t_i-\bar{t}\right)y_i}{\Sigma\left(t_i-\bar{t}\right)^2}$ ，其中， $\bar{t}$ 是干预的群体样本平均数， $\bar{y}$ 是干预结果的群体样本平均数。

要对单变量回归的斜率参数估计进行编码，可以使用 curry。当你需要创建接受数据帧作为唯一参数的函数时，它非常有用：

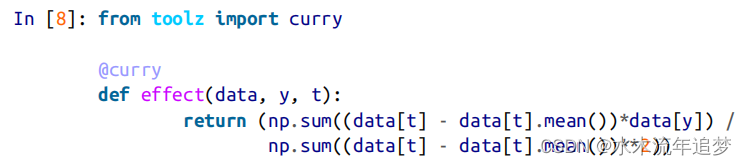
将此函数应用于整个测试集，即可得到 ATE：

python">effect(test, "sales", "discounts")

但这并不是您想要的。相反，您想知道您刚刚拟合的模型能否在数据中创建分区，将单位从对干预更敏感的单位中分离出来。为此，您可以按照模型预测值的量级来划分数据，并估计每个量级的效果。如果每个量级的估计效果都是有序的，那么就说明该模型也能很好地对真实的 CATE 进行排序。

让我们编写一个函数来计算量化效应。它首先使用 pd.qcut 按 q 个量化值（默认为 10）分割数据。我将它封装在 pd.IntervalIndex 中，以提取 pd.qcut 返回的每个组的中点。四舍五入只是为了让结果看起来更漂亮。然后，我将在数据中创建一列包含这些组的数据，用它们对数据进行分区，并估算每个分区的效果。在最后一步，我使用了 pandas 的 .apply(...) 方法。该方法接收一个以数据帧为输入的函数，并输出一个数字：f(DataFrame) -> float。这就是你之前创建的效果函数发挥作用的地方。您可以只通过干预和治疗参数来调用它。这将返回一个部分应用的效应函数，数据帧是唯一缺少的参数。这就是 .apply(...) 所期望的函数类型。

在test_pred数据框架中使用此函数的结果是一列，其中索引是模型预测的分位数和值，以及该分位数中的处理效果：

python">def effect_by_quantile(df, pred, y, t, q=10):# makes quantile partitionsgroups = np.round(pd.IntervalIndex(pd.qcut(df[pred], q=q)).mid, 2)return (df.assign(**{f"{pred}_quantile": groups}).groupby(f"{pred}_quantile")# estimate the effect on each quantile.apply(effect(y=y, t=t)))effect_by_quantile(test_pred, "cate_pred", y="sales", t="discounts")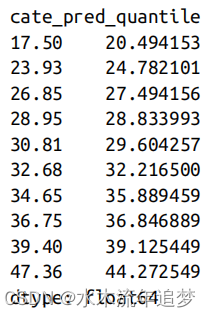

注意第一分位数的估计效应如何低于第二分位数的估计效应，后者低于第三分位数的估计效应，以此类推。这证明了你的CATE预测确实是排序效应的：预测值较低的日子对折扣的敏感性也较低，反之亦然。此外，每个分位数的中点预测（前一列中的指数）非常接近于相同分位数的估计效果。这意味着您的CATE模型不仅很好地排序了真正的CATE，而且还能准确地预测它。换句话说，您有一个针对CATE的校准模型。

接下来，您有其他模型进行比较，您可以应用相同的函数，但是传递预测ML模型和随机模型。下图显示了前面定义的三个模型的分位数效果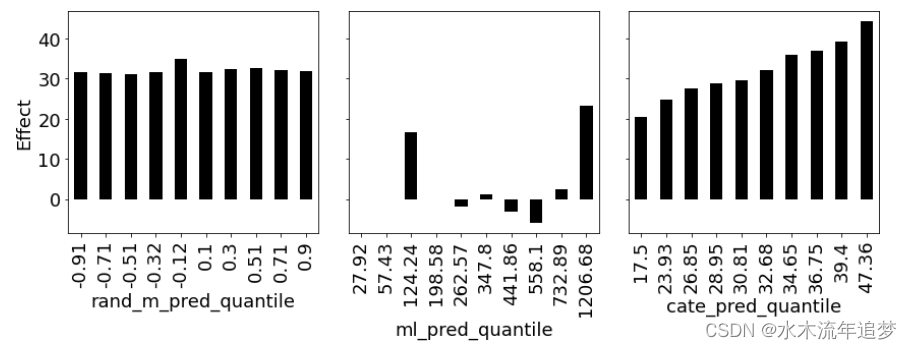：首先，看看随机模型（rand_m_pred）。它在每个分区中具有大致相同的估计效果。你已经可以通过看情节看到，它不会帮助你的个性化，因为它不能区分高折扣和低折扣敏感度的日子。在它的所有分区中，所产生的效果都只是ATE。接下来，考虑ML预测模型，ml_pred。这个模型更有趣一些。看起来，有高销售预测和低销售预测的群体都对折扣更为敏感。不过，它并不能完全产生订购分数，但你可以使用它进行个性化，也许当销售预测非常高或非常低时给予更多的折扣，因为这表明治疗敏感性很高.

最后，看看你从回归中得到的CATE模型，cate_pred。低CATE预测组的CATE确实低于高CATE预测组。看起来这个模型可以很好地区分高效果和低效果。你可以通过一个分位数图的楼梯形状来判断它的效果。一般来说，楼梯的形状越陡，模型的CATE排序就越好。

在这个例子中，很清楚哪个模型在对折扣的排序敏感性方面更好。但如果你有两个像样的模型，比较可能没有那么明确。此外，可视化验证也很好，但如果您想进行模型选择（如超参数调优或特征选择），那么它就不理想了。理想情况下，您应该能够用一个数字来总结模型的质量。我们会做到的，但要做到这一点，你首先需要了解累积效应曲线。

Cumulative Effect

如果你用分位数图来理解效果，下一个就会很容易了。同样，这个想法是使用您的模型来定义组并估计组内部的效果。但是，您不是按组估算效果，而是将一组累加到另一组之上。

首先，您需要按分数对数据进行排序——通常是一个CATE模型，但它确实可以是任何东西。然后，你将根据这个顺序来估计对前1%的影响。接下来，你将添加下面的1%，并计算对前2%的影响，然后计算前3%，以此类推。结果将是累积样本的效应曲线。这里有一个简单的代码：

python"> def cumulative_effect_curve(dataset, prediction, y, t,ascending=False, steps=100):size = len(dataset)ordered_df = (dataset.sort_values(prediction, ascending=ascending).reset_index(drop=True))steps = np.linspace(size/steps, size, steps).round(0)return np.array([effect(ordered_df.query(f"index<={row}"), t=t, y=y)for row in steps])cumulative_effect_curve(test_pred, "cate_pred", "sales", "discounts")

如果您用来对数据进行排序的分数也能很好地对真实 CATE 进行排序，那么得到的曲线将从很高的位置开始，然后逐渐下降到 ATE。与此相反，如果模型不好，要么会很快收敛到 ATE，要么就一直在 ATE 附近波动。为了更好地理解这一点，下面是您创建的三个模型的累积效应曲线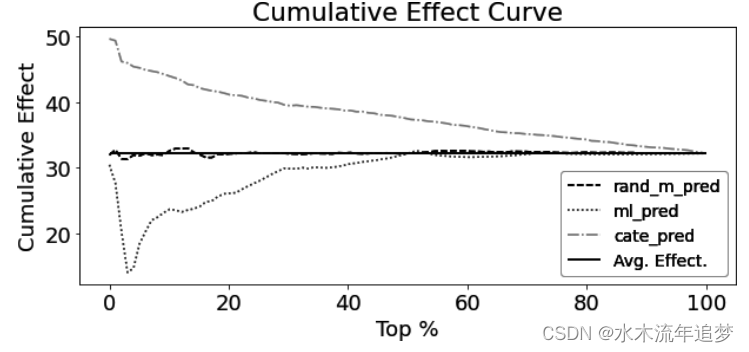：首先，注意回归CATE模型是如何非常高，逐渐接近ATE的。例如，如果您按这个模型对数据进行排序，则在前20%在42岁左右，前50%的ATE在37岁左右，而前100%的ATE将只是治疗的全体效果（ATE）。相比之下，一个简单地输出随机数的模型只会围绕着ATE展开，而一个反向排序效果的模型将在ATE下方开始。

累积效应曲线比量化效应曲线要好一些，因为它可以总结为一个单一的数字。例如，您可以计算曲线与 ATE 之间的面积，并以此来比较不同的模型。面积越大，模型越好。但这样做还是有弊端。如果这样做，曲线起点的面积会最大。但由于样本量较小，这正是不确定性最大的地方。幸运的是，有一个非常简单的解决方法：累积增益曲线。