本文主要介绍概率极限理论中的大数定律,内容包括:

1. Chebyshev弱大数定律, 三角阵列的弱定律(截断方法)得到的Khinchin弱大数定律;

2. 强大数定律的两种证明方法: 由Borel-Cantelli引理得到的强大数定律, 随机级数收敛方法得到的强大数定律. 此外给出了更新理论和大偏差理论.

1. 独立性的定义

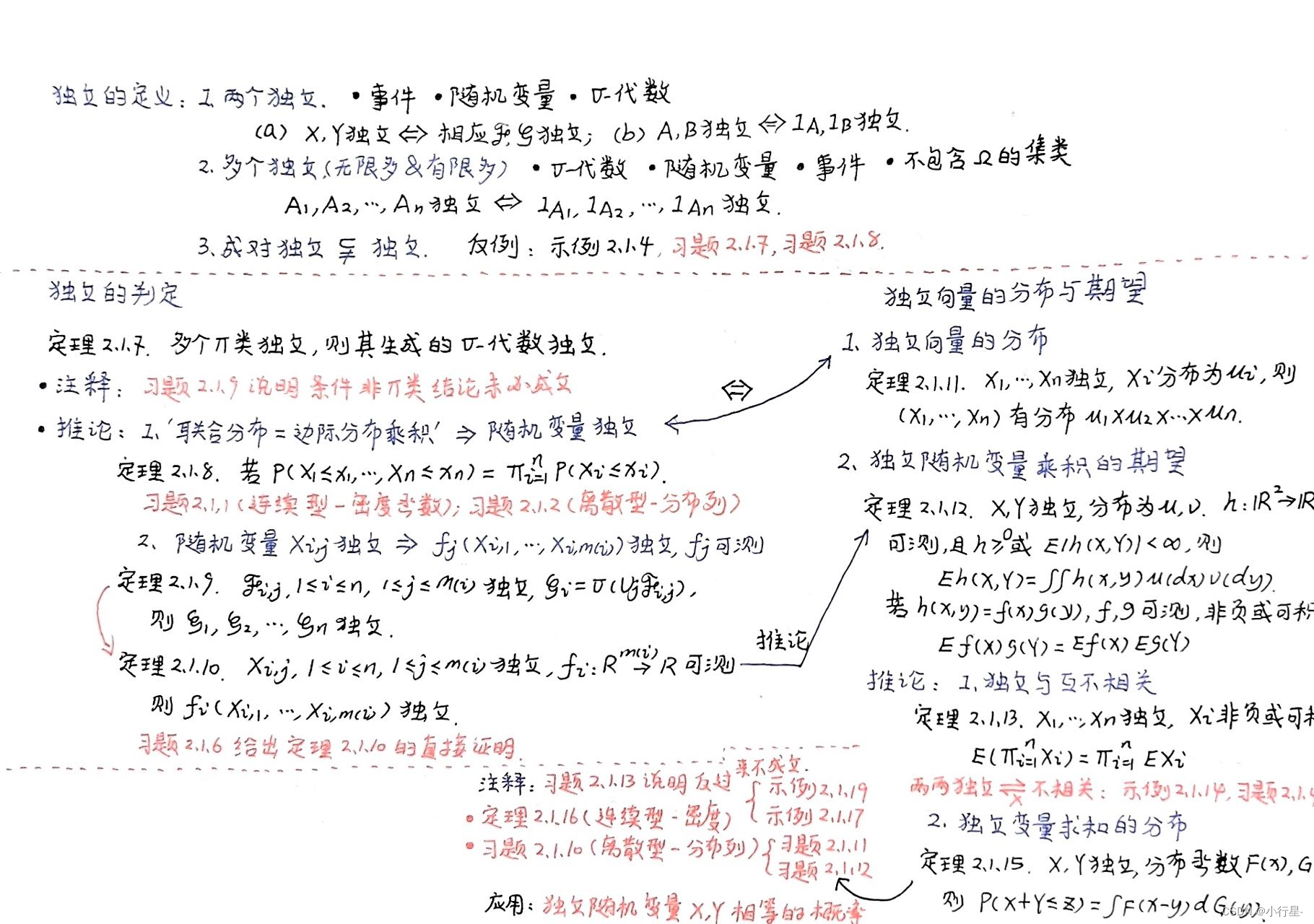
概率论与测度论的分水岭: 引入条件概率与独立性这两个概念意味着测度论的终结, 概率论的开始.测度论是研究概率的一种工具(例如可以用纯代数的方法研究概率:Free probability), 因此概率论中最重要的概念本质上不依赖于测度. 下面是本节-独立性的思维导图.

• 两个事件独立,两个随机变量独立,两个 $\sigma$-代数独立的定义; 三者之间的关联:4. 两个事件独立是两个随机变量独立的特殊情况(定理2.1.2); 2. 两个随机变量独 立是两个 $\sigma$-代数独立的特殊情况(定理 2.1.1).

• 多个事件独立,多个随机变量独立,多个 $\sigma$-代数独立的定义;三者之间的关联:

• 多个随机变量独立是多个 $\sigma$-代数独立的特殊情况(定理2.1.3).

1.1. 两个事件、两个随机变量、两个 $\sigma$-代数独立

定义 (两个事件、两个随机变量、两个 $\sigma$-代数独立)

• (i) 若$P(A\cap B)=P(A)P(B)$ ,则两个事件 $A$ 和 $B$ 是独立的;\
• (ii) 两个随机变量 $\mathrm{X}$ 和 $\mathrm{Y}$ 是独立的, 如果对于所有的 $C,D\in R$
  $$P(X\in C,Y\in D)=P(X\in C)P(Y\in D)$$
  即事件 A = { X ∈ C } A=\{X \in C\} A={X∈C} 和 B = { Y ∈ D } B=\{Y \in D\} B={Y∈D} 是独立的.\
• (iii) 若对所有$A\in \mathcal{F}$, $B\in \mathcal{G}$, 事件$A$和$B$都是独立的, 则两个$\sigma$-代数 $\mathcal{F}$, $\mathcal{G}$独立.

定理2.1.1 (随机变量独立与$\sigma$代数独立的关系)]

• (i) 若$X$,$Y$独立, 则$\sigma (\mathrm{X})$, $\sigma (\mathrm{Y})$独立.
• (ii) 若$\mathcal{F}$,$\mathcal{G}$ 独立, $X\in \mathcal{F}$, $Y\in \mathcal{G}$, $X$,$Y$独立.

证明：根据定义证明即可.

定理 2.1.2 (事件独立与随机变量独立的关系)

• (i) 若$A$,$B$独立, 则$A^c$和$B$, $A$和$B^c$, $A^c$和$B^c$也独立.\
• (ii) 相反,事件 $A$ 和 $B$独立, 当且仅当它们的示性随机变量 $1_A$,$1_B$独立.

将其简化为有限多对象的情况,即如果每个有限子集合中的对 象都独立,那么无限集合中的对象( $\sigma$代数、随机变量或集合)就是独立的.

1.2. 多事件、多个$\sigma$-代数、多个随机变、多个事件独立

定义 (无穷多事件、多个$\sigma$-代数、多个随机变、多个事件独立)
(i) 多个 $\sigma$-代数 ${\mathcal{F}}_1,{\mathcal{F}}_2,\dots ,{\mathcal{F}}_n$ 独立,如果任意 $A_i\in {\mathcal{F}}_i,$ 对 $i=1,\dots ,n$ ,有
$$P\left({\cap }_{i=1}^n{A}_i\right)=\prod _{i=1}^{n}P\left(A_i\right)$$
(ii) 随机变量 $X_1,\dots ,X_n$ 独立,如果对 $i=1,\dots ,n$ ,任意 $B_i\in \mathcal{R}$ 有
P ( ∩ i = 1 n { X i ∈ B i } ) = ∏ i = 1 n P ( X i ∈ B i ) P\left(\cap_{i=1}^{n}\left\{X_{i} \in B_{i}\right\}\right)=\prod_{i=1}^{n} P\left(X_{i} \in B_{i}\right) P(∩i=1n​{Xi​∈Bi​})=i=1∏n​P(Xi​∈Bi​)
(iii) 集合 $A_1,\dots ,A_n$ 独立如果任意 I ⊂ { 1 , … n } I \subset\{1, \ldots n\} I⊂{1,…n} 有$P\left({\cap }_{i\in I}{A}_i\right)={\prod }_{i\in I}P\left(A_i\right)$.

定理2.1.3 (多个事件独立与多个随机变量独立的关系) 令 $A_1,A_2,\dots A_n$ 独立. (i) $A_1^c,A_2,\dots ,A_n$ 是独立的; (ii) $1_{A_1},\dots ,1_{A_n}$ 是独立.

1.3. 成对独立和独立的关系

示例2.1.4与习题2.1.7,习题2.1.8):独立的事件是成对独立的,而相反是不正确的 三个随机变量独立,而有了第四个不独立的例子.

2. 独立性的充分条件

证明多个随机变量独立等价于联合分布等于边际分布的乘积.

为证明随机变量X和Y是独立的,必须检查所有Borel集合A和B独立,直接证明过于繁琐,有必要给出一些充分性条件(定理2.1.7).

引理2.1.5 (sigma代数并上全集后的独立性) 集类 A 1 ∪ { Ω } , A 2 ∪ { Ω } , … , A n ∪ { Ω } ⊂ F \mathcal{A}_{1} \cup\{\Omega\}, \mathcal{A}_{2} \cup\{\Omega\}, \ldots, \mathcal{A}_{n} \cup\{\Omega\} \subset \mathcal{F} A1​∪{Ω},A2​∪{Ω},…,An​∪{Ω}⊂F 独立,对任意 $A_i\in {\mathcal{A}}_i$ ,
$$P\left({\cap }_{i=1}^n{A}_i\right)=\prod _{i=1}^{n}P\left(A_i\right)$$

定理2.1 .7 (各独立pi类生成的sigma代数独立) 假设 ${\mathcal{A}}_1,{\mathcal{A}}_2,\dots ,{\mathcal{A}}_n$ 独立,任意 ${\mathcal{A}}_i$ 是 $\pi$ 类. 则 $\sigma \left({\mathcal{A}}_1\right),\sigma \left({\mathcal{A}}_2\right),\dots ,\sigma \left({\mathcal{A}}_n\right)$ 独立.

习题2.1.9 两个集类独立,生成的$\sigma$代数不独立

推论2.1 .8 (随机变量独立只需分布函数独立性) 为让 $X_1,\dots ,X_n$ 独立,只要对所有 $x_1,\dots ,x_n\in (-\infty ,\infty ]$ 有
$$P\left(X_1\le x_1,\dots ,X_n\le x_n\right)=\prod _{i=1}^{n}P\left(X_i\le x_i\right)$$

习题2.1.1和2.1.2 密度函数和离散随机变量的独立性

假设 $X_1,\dots ,X_n$ 是独立随机变量,且 $X_i$ 有分布 ${\mu }_i$ ,则 $\left(X_1,\dots ,X_n\right)$ 有分布 ${\mu }_1\times \cdots \times {\mu }_n$.

3. 独立向量的分布和期望

首先给出第一节【独立性的第二个判定方法】(第一个判别法推论),即独立随机变量的不相交集合的函数是独立的(定理2.1.10),以此证明两个独立的随机变量意味着不相关(定理2.1.12,定理2.1.13),不过互不相关的随机变量不一定相互独立.

3.1. 独立向量的分布

引理 2.1.9 假设 ${\mathcal{F}}_{i,j},1\le i\le n,1\le j\le m(i)$ 独立,令 ${\mathcal{G}}_i=\sigma \left({\cup }_j{\mathcal{F}}_{i,j}\right)$. 则 ${\mathcal{G}}_1,\dots ,{\mathcal{G}}_n$ 独立.

定理 2.1.10(独立随机变量的不相交集合的函数独立) 若 $1\le i\le n,1\le j\le m(i),X_{i,j}$ 独立, $f_i:{\mathbf{R}}^{m(i)}\to \mathbf{R}$ 可测,则 $f_i\left(X_{i,1},\dots ,X_{i,m(i)}\right)$ 独 立.

习题2.1.6 从定义的方法直接得出两个独立随机变量各自可测函数独立.

如果 $X_1,\dots ,X_n$ 是独立的,那么 $X=X_1$ 和 $Y=X_2\cdots X_n$ 是独立的.

独立随机变量 $X_1,\dots ,X_n$ “和” $S_m=X_1+\cdots +X_m$ ,由定理2.1.10,那么 $S_n-S_m$ 独立于事件
$$\left\{\underset{1\le k\le m}{\max }{S}_k>x\right\}$$
的示性函数.

3.2. 独立随机变量乘积期望

定理2.1.12 (多维独立随机变量函数的期望) 假设 $X$ 和 $Y$ 独立,并且有分布 $\mu$ 和 $\nu$. 若 $h:{\mathbf{R}}^2\to \mathbf{R}$ 是可测函数, $h\ge 0$ 或 $E|h(X,Y)|<\infty$ ,则
$$Eh(X,Y)=\iint h(x,y)\mu (dx)\nu (dy)$$
特别地,如果 $h(x,y)=f(x)g(y)$ ,其中 $f,g:\mathbf{R}\to \mathbf{R}$ 可测, $f,g\ge 0$ 或 $E|f(X)|$ 和 $E|g(Y)|<\infty$ 则
$$Ef(X)g(Y)=Ef(X)\cdot Eg(Y)$$

习题2.1.14 计算独立随机变量乘积的分布函数

3.2.1. 独立的随机变量意味着不相关

推论2.1.13 独立的随机变量意味着不相关 如果 $X_1,\dots ,X_n$ 独立,且(a) 对所有 $i$ $X_i\ge 0$ ,或(b) 对所有 $i,E\left|X_i\right|<\infty$ ,则
$$E\left(\prod _{i=1}^n{X}_i\right)=\prod _{i=1}^{n}E{X}_i$$

举例2.1.14和习题2.1.4 说明不相关的随机变量不一定独立.

不相关 一个随机变量族 $X_i,i\in I$ 和 $E{X}_i^2<\infty$ ,如果是不相关的 $E\left(X_i{X}_j\right)=E{X}_{i}E{X}_{j_1}$ 任意 $i\ne j$.

3.2.2. 独立随机变量和的分布

定理2.1.12的推论, 得到多个独立随机变量和的分布公式(定理2.1.15,定理2.1.16)

定理 2.1.15 (独立随机变量和的分市函数) 若 $X$ 和 $Y$ 独立, $F(x)=P(X\le x)$ ,且 $G(y)=P(Y\le y)$ ,则
$$P(X+Y\le z)=\int F(z-y)dG(y)$$
右侧积分称为 $F$ 和 $G$ 的卷积,定义为 $F\ast G(z)$.

习题2.1.13 $X$ 和 $Y$ 不独立,同样也能满足上述公式的例子.

特例2.1.16 (独立随机变量和的分布) 假设 $X$ 有密度 $f,Y$ 分布函数为 $G$ ,两者相互 独立. 则 $X+Y$ 有密度
$$h(x)=\int f(x-y)dG(y)$$
当 $Y$ 有密度 $g$ ,上式可写为 $h(x)=\int f(x-y)g(y)dy$

习题2.1.5推出两个独立随机变量求和为 0 的概率公式,且证得具有连续分布的独立随机变量相等的概率为 0.

习题2.1.10推出两个独立整数值随机变量求和为 $n$ 的概率公式.

两个标准的例子:多个独立伽马分布随机变量和的分布,多个独立高斯分布随机变量和的分布.

习题2.1.11和习题2.1.12 利用习题2.1.10证明两个独立Poission分布随机变量和的分布.\
利用习题2.1.10证明多个独立Binomial分布随机变量和的分布.

4. 独立随机变量的存在性

4.1. 有限个独立随机变量的构造

给定有限个随机变量的分布函数 $F_i,1\le i\le n$ ,容易构造带有分布函数 $P\left(X_i\le x\right)=F_i(x)$ 的 $X_1,\dots ,X_n$.

有限个独立随机变量的构造 令 $\Omega ={\mathbf{R}}^n,\mathcal{F}={\mathcal{R}}^n,X_i\left({\omega }_1,\dots ,{\omega }_n\right)={\omega }_i(\omega \in {\mathbf{R}}^n$ 的 $i$ 个坐标 $)$ ,令 $P$ 是 ${\mathcal{R}}^n$ 上 的测度,有
$$P\left(\left(a_1,b_1\right]\times \cdots \times \left(a_n,b_n\right]\right)=\left(F_1\left(b_1\right)-F_1\left(a_1\right)\right)\cdots \left(F_n\left(b_n\right)-F_n\left(a_n\right)\right)$$
若 ${\mu }_i$ 是有分布函数 $F_i$ 的测度,则 $P={\mu }_1\times \cdots \times {\mu }_n$.

4.2. 无穷个独立随机变量的构造

为构造无穷多个带有分布函数的独立随机变量 $X_1,X_2,\dots$ ,我们想把有限维的方法用到无穷维 上
R N = { ( ω 1 , ω 2 , … ) : ω i ∈ R } = { functions  ω : N → R } \mathbf{R}^{\mathbf{N}}=\left\{\left(\omega_{1}, \omega_{2}, \ldots\right): \omega_{i} \in \mathbf{R}\right\}=\{\text { functions } \omega: \mathbf{N} \rightarrow \mathbf{R}\} RN={(ω1​,ω2​,…):ωi​∈R}={ functions ω:N→R}
其中, N = { 1 , 2 , … } , N \mathbf{N}=\{1,2, \ldots\} , \mathbf{N} N={1,2,…},N 是自然数.

无穷个独立随机变量的构造 定义 $X_i(\omega )={\omega }_i$ ,配备 ${\mathbf{R}}^{\mathbf{N}}$ 以乘积 $\sigma$-代数 ${\mathcal{R}}^{\mathbf{N}}$ ,这 由形式为 { ω : ω i ∈ B i , 1 ≤ i ≤ n } \left\{\omega: \omega_{i} \in B_{i}, 1 \leq i \leq n\right\} {ω:ωi​∈Bi​,1≤i≤n} 的有限维集合生成,其中, $B_i\in \mathcal{R}$. 为把有限维 $P$ 存在性 拓展到无穷维的 ${\mathcal{R}}^{\mathrm{N}}$ ,需要科尔莫戈罗夫延拓定理.

习题2.1.15 可以不用科尔莫戈罗夫延拓定理构造出抛硬币的无穷序列

其他可测空间的情形下,科尔莫戈罗夫延拓定理不成立,

无穷个取值于其他可测空间的独立随机变量的构造 有一类nice空间足以满足我们所有的结果,即科尔莫戈罗夫定理在这一空间的推广是自然的.

nice空间 $(S,\mathcal{S})$ 被称为nice空间,如果存在从 $S$ 到 $\mathbf{R}$ 的 $1-1$ 映射 $\phi$ 使得 $\phi$ 和 ${\phi }^{-1}$都可测.

这样的空间通常被称为标准的Borel空间,下一个结果表明,在应用中产生的大多数空间都是很好(nice)的.

定理2.1.22 (nice空间的判定) 如果 $S$ 是完备可分度量空间 $M$ 的Borel子集,且 $\mathcal{S}$ 是 $S$ 的Borel子集的集合,则 $(S,\mathcal{S})$ 是 nice空间.

该分析的一个有趣的结果是,对于一个完全可分度量空间的Borel子集,连续体假设是正确的:即所有的集要么是有限的、可数无限的,要么是具有实数的基数.