拿捏AVL（C++）

ops/2024/10/9 15:15:26/

文章目录

  • 前言
  • AVL树介绍
  • 模拟实现
    • 框架
    • 查找
    • 插入
    • 验证
    • 删除
    • 完整代码
  • 性能分析
  • 总结

前言

在本篇文章中我，我们将会介绍一下·有关AVL树的相关内容，并且对一些接口进行模拟实现。

AVL树介绍

为什么会有AVL树呢？？
我们在之前学习二叉树时，如果我们插入的顺序是有序或者接近有序，就会退化成单支，查找一个值的时间复杂度就是O（N）。

为了解决这个问题，因此，两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年
发明了一种解决上述问题的方法：

插入每个节点时，保证左右子树的高度差的绝对值不超过1，从而降低高度，保证平衡。

为什么保证高度不超过1呢？？为0不是更平衡吗？？
我们的节点是一个个插入的，有些情况无法做到左右子树高度不超过1，比如只有两个节点，4个节点。

一棵AVL树或者是空树，或者是具有以下性质的二叉搜索树：
🌟 它的左右子树都是AVL树
🌟 左右子树高度之差(简称平衡因子)的绝对值不超过1

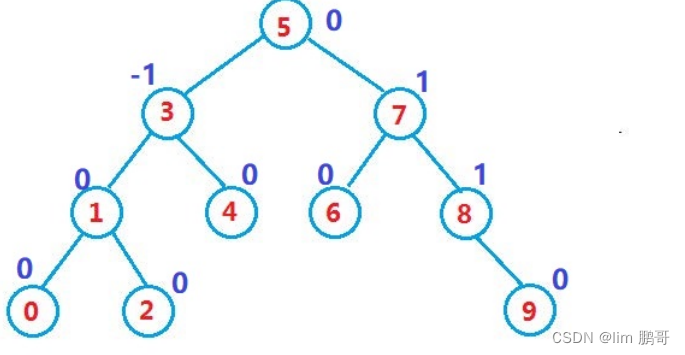
在这里插入图片描述
这里引入平衡因子并不是必须的，而只是一种实现方式，方便我们理解，我们在进行模拟实现的时候，也会采用平衡因子的方式。

如果一颗二叉搜索树是高度平衡的，就是AVL树。
如果有N个节点，高度可保持在logN,搜索时间复杂度O（logN）

模拟实现

框架

每个节点都要包含一个平衡因子，并且加入一个父亲节点，方便我们进行链接。
这是一个三叉链的结构。

template<class K,class V>
struct AVLTreeNode
{AVLTreeNode(const pair<K,V>kv):_left(nullptr), _right(nullptr), _parent(nullptr),_kv(kv), _bf(0){ }AVLTreeNode<K, V> *_left;AVLTreeNode<K, V>*_right;AVLTreeNode<K, V>*_parent;pair<K, V>_kv;int _bf;//平衡因子
};template<class K,class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:private:Node* _root = nullptr;
};

查找

我们查找的逻辑和二叉树的逻辑类似，这里就不在过多叙述了。
我们这里采用的是KV结构，需要返回查找的节点。
如果找不到，就返回nullptr

	Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_kv.first < key){cur = cur->_right;}else if (cur->_kv.first > key){cur = cur->_left;}else{return cur;}}return NULL;}

插入

我们如何进行插入呢？？？

🌟 按照搜索二叉树规则插入节点
🌟 更新平衡因子

寻找插入节点很容易解决，我们重点看一下平衡因子的更新。

我们这里规定平衡因子=右子树的高度–左子树高度

如果我们插入的节点在父节点的左边，父节点的平衡因子就减减
如果我们插入的节点在父节点的右边，父节点的平衡因子就加加

我们是否要继续向上更新呢？？
是否继续更新去接与树的高度是否发生变化，插入节点可能会影响这个节点的祖先节点

我们对父节点的平衡因子进行更新后，可能会遇到以下情况
🌟 父节点的平衡因子为0。此时说明树的高度已经平衡了，不需要继续调整。说明之前父节点的平衡因子为-1或者1，我们在矮的那边1进行了插入，这是树的高度达到平衡。

🌟 父节点的平衡因子为-1或者1。说明之前树的高度平衡，父节点的平衡因子为0。我们在一边进行插入。树的高度发生了变化，不确定是否继续影响爷爷节点，我们不能结束，需要继续判断。
cur=parent;
parent=parent->_parent

🌟 父节点的平衡因子为2或者-2，违反了我们的规则，需要进行调整，我们调整的策略就是旋转。旋转之后树的高度达到了平衡，无需继续更新。

🌟如果我们更新到了根节点也结束

bool Insert(const pair<K, V>kv)
{//按照二叉搜索树规则插入if (_root == nullptr){_root = new Node(kv);return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_kv. first> kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(kv);cur->_parent = parent;if (kv.first > parent->_kv.first){parent->_right = cur;}else{parent->_left = cur;}//更新平衡因子//更新规则：右子树高度--左子树高度//更新到根节点结束while (parent)//cur在根结束{if (cur == parent->_left){parent->_bf--;}else{parent->_bf++;}//分三种情况if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}//进行旋转else if (parent->_bf == 2 || parent->_bf == -2){//旋转break;}}return true;
}

我们进行旋转
1.保持原来搜索树规则不变
2.降低树的高度
3.由不平衡变为平衡

左旋(cur->_bf = = 1 && parent->_bf = = 2)

什么情况下我们会进行左旋呢？？
如果右子树的右边高，我们就进行左旋

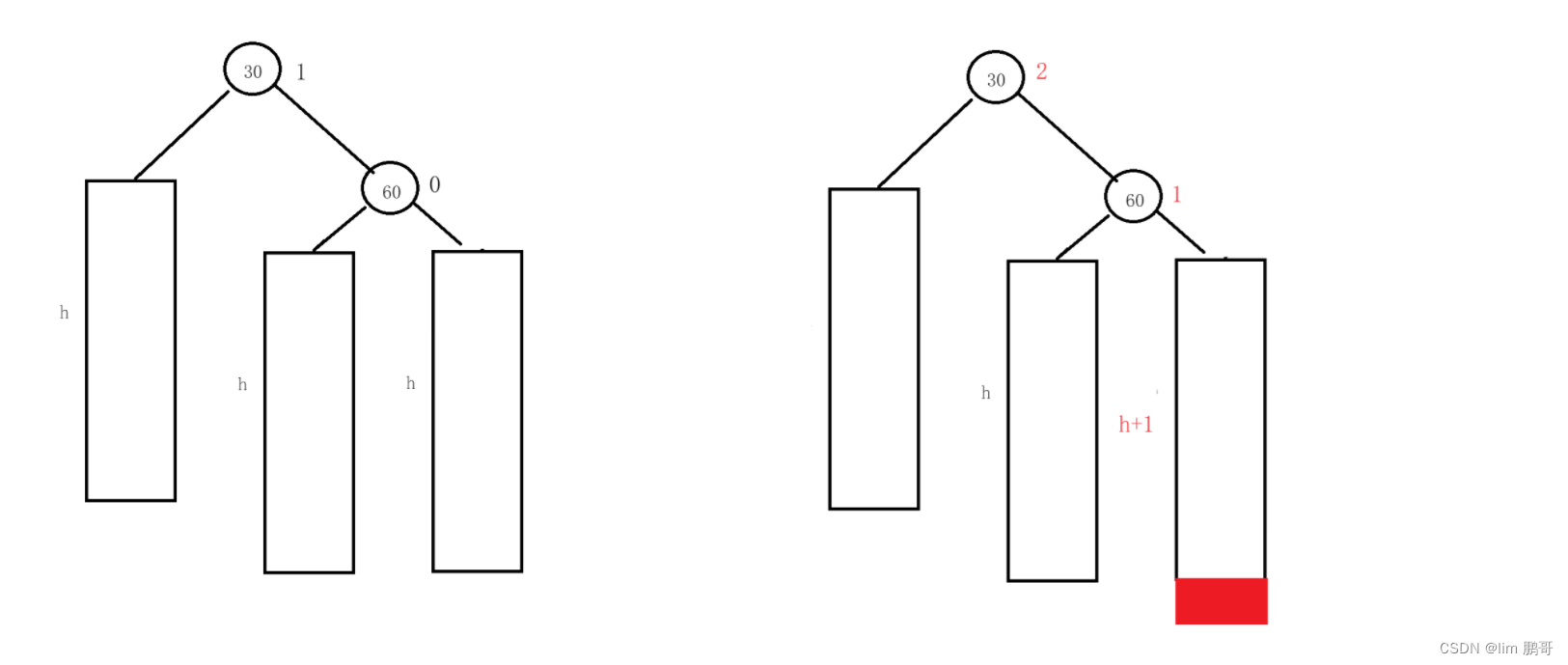
在这里插入图片描述
我们为什么要画一个这样的图？？？？

我们对h进行赋值，看一下

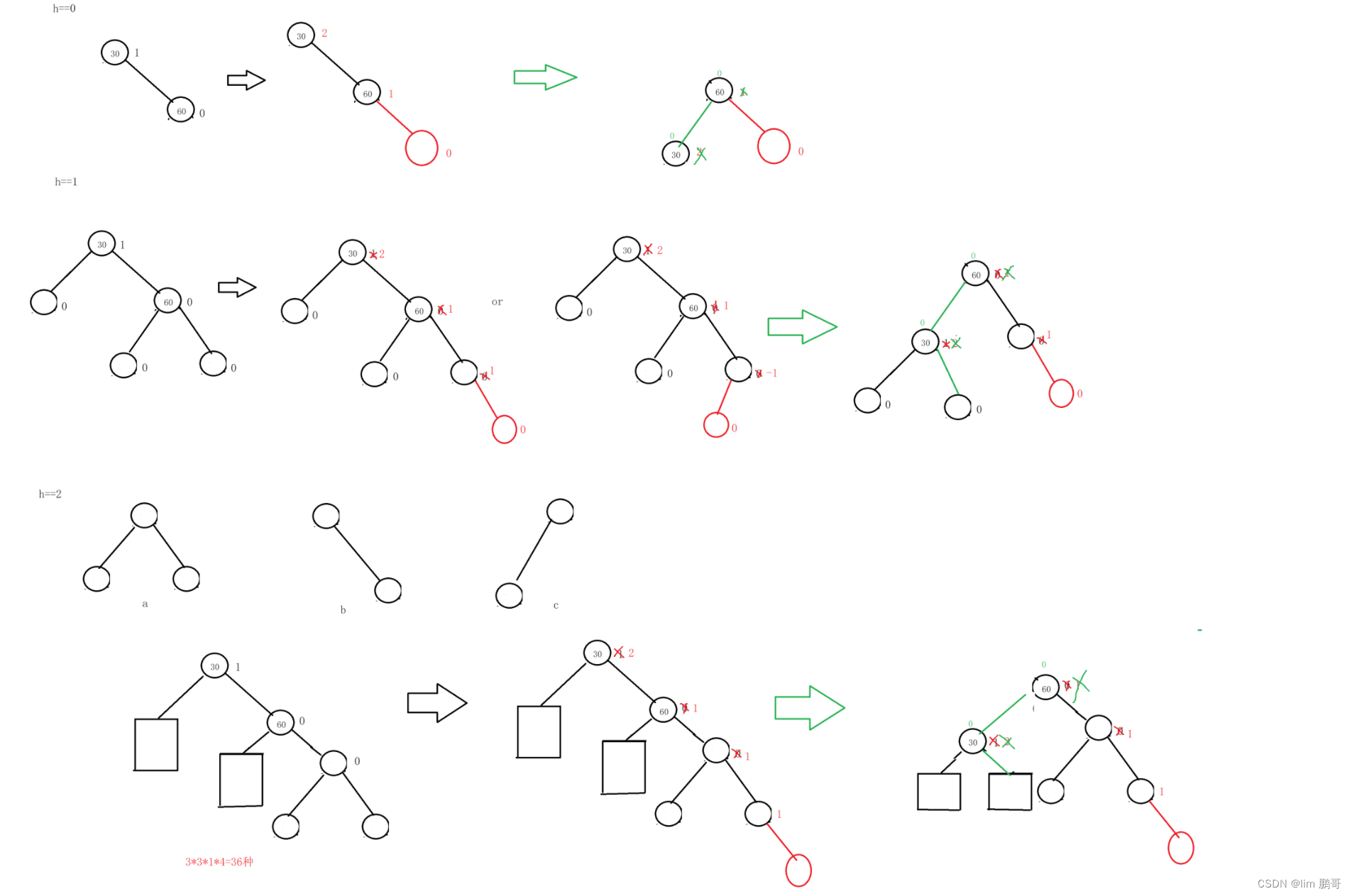
h==0
只有一种情况
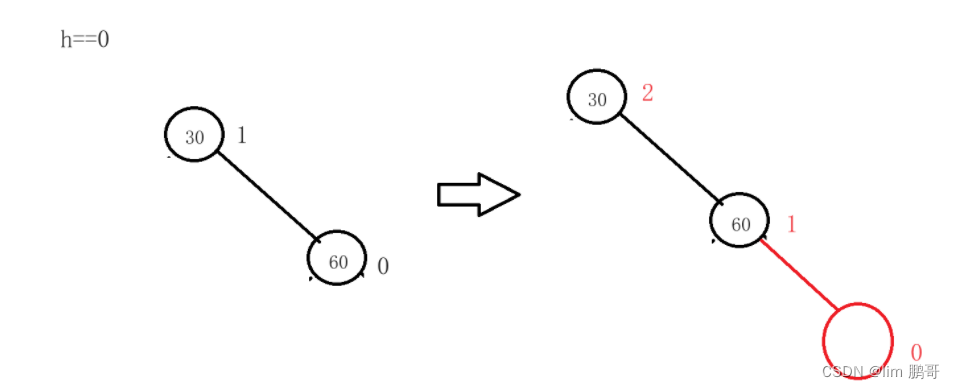
在这里插入图片描述

h==1;
我们有两个位置可以进行插入，有两种情况。
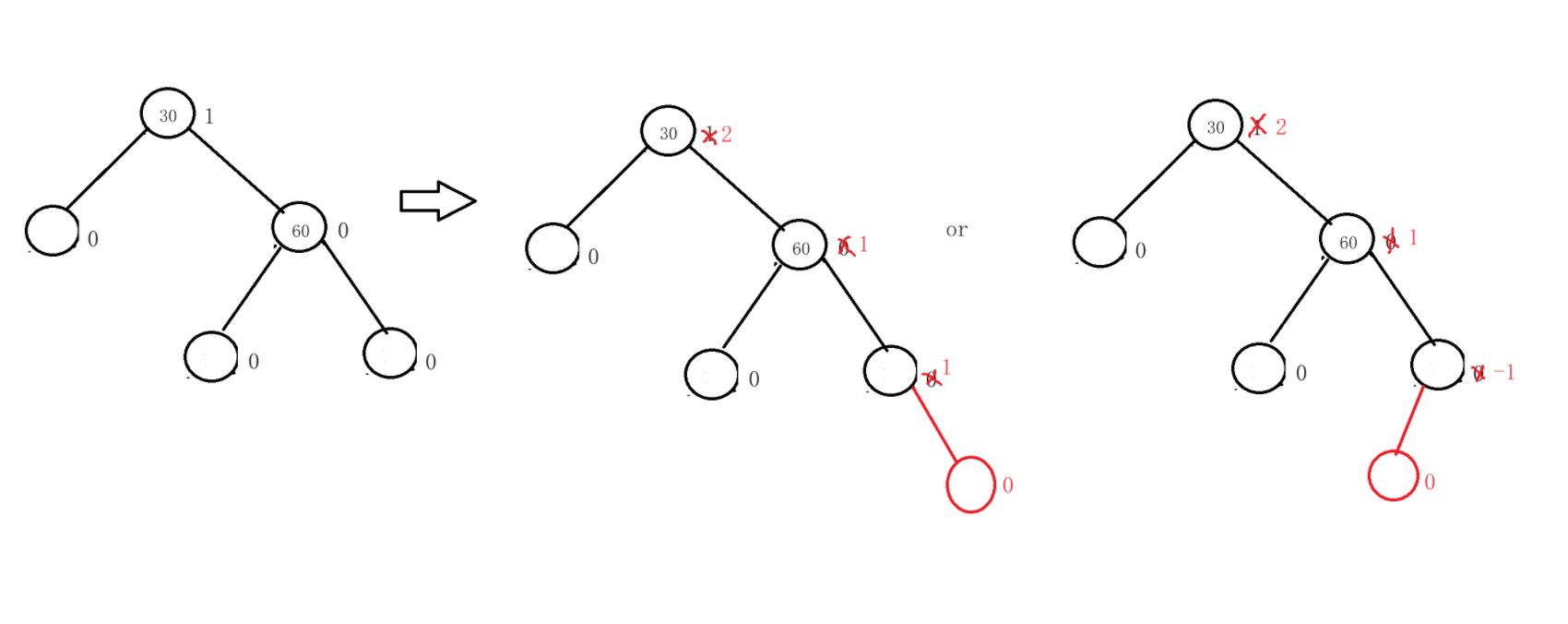
在这里插入图片描述

h==2

h==2的树有三种情况
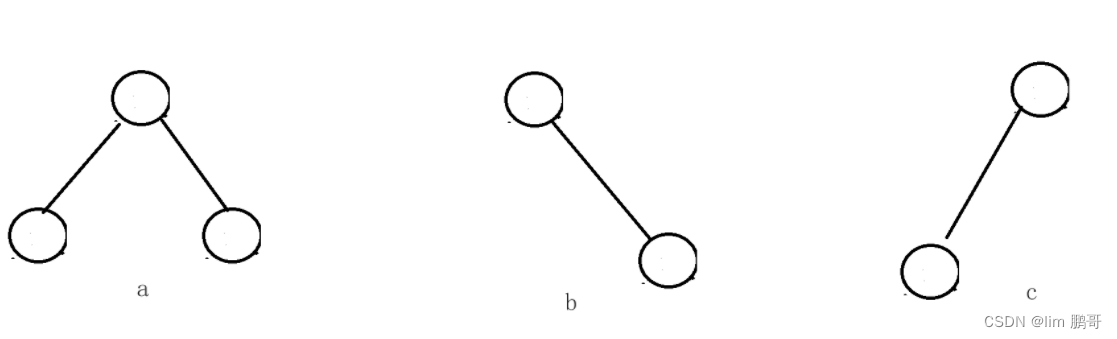
在这里插入图片描述

我们用长方形代替了a,b，c情况中的一种
两个长方形都有三种选择，插入位置有四种选择，331*4=36。
这就有36种情况了，如果我们一个个分析，是分析不完的。

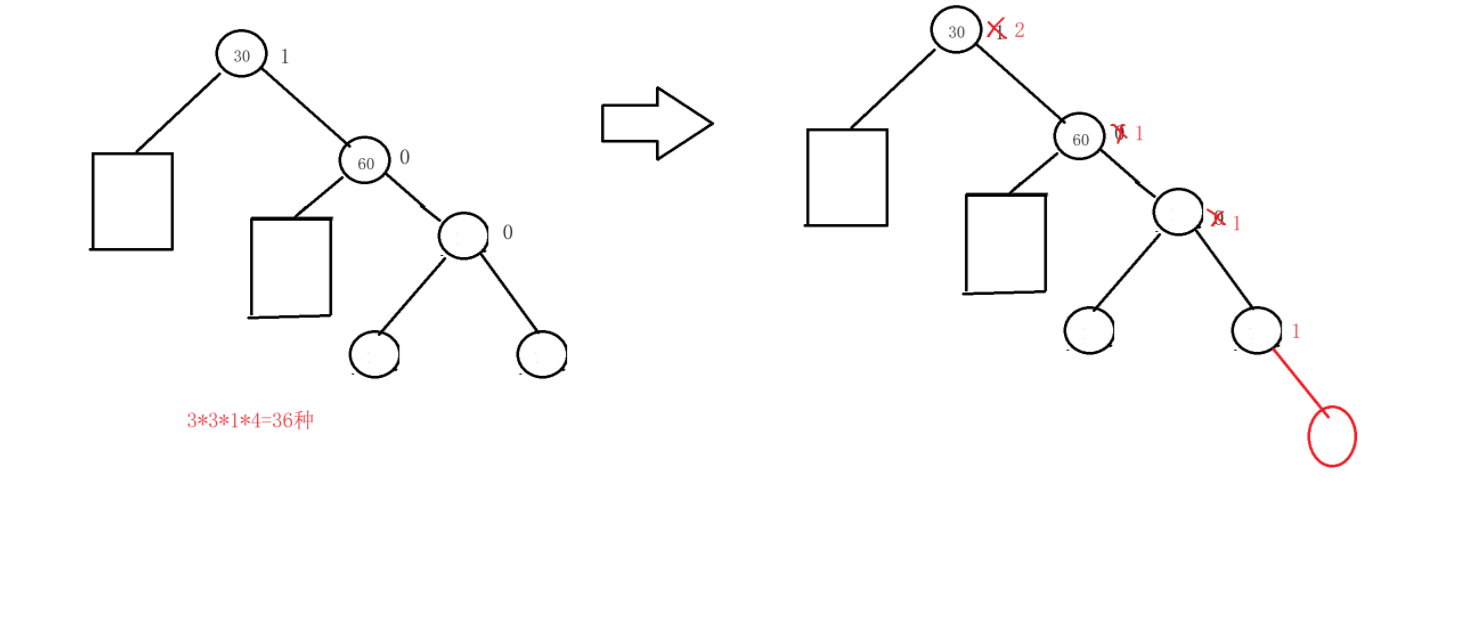
在这里插入图片描述
我们可以发现这几个例子中都有共同点
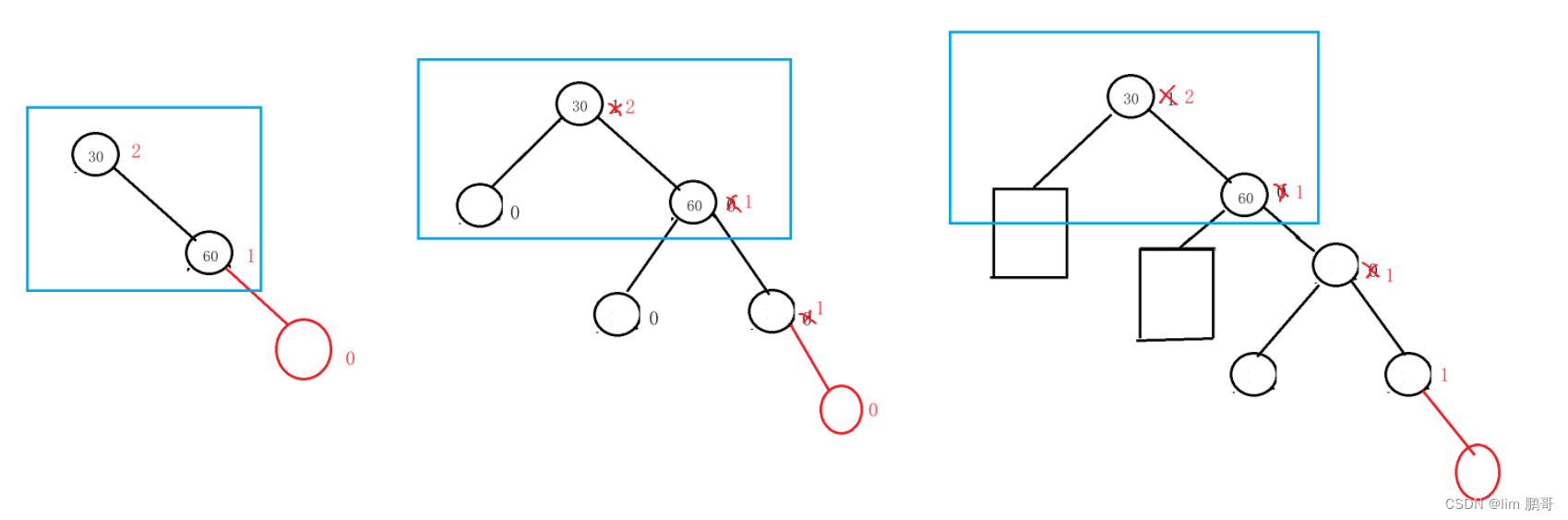
在这里插入图片描述

所以我们把它划分为一类，就如下图所示
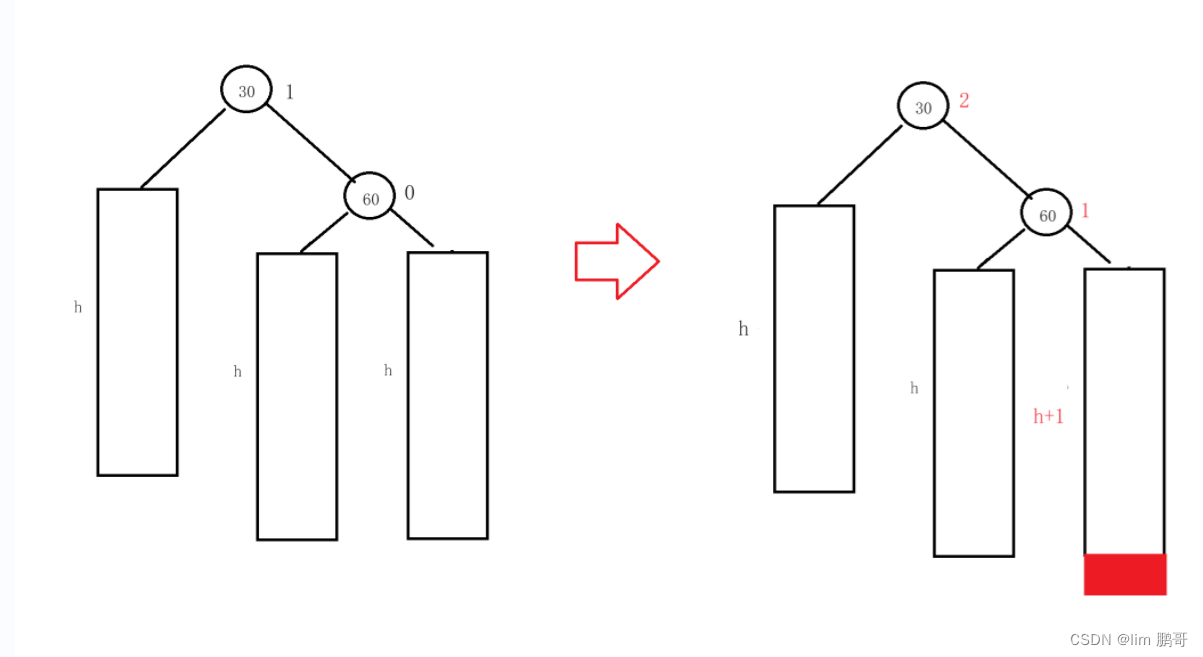
在这里插入图片描述
我们如何进行旋转呢？？
如图所示，将30的右子树连接到60的左子树上；60的左子树连接上30，让60做这棵树的根，更新平衡因子

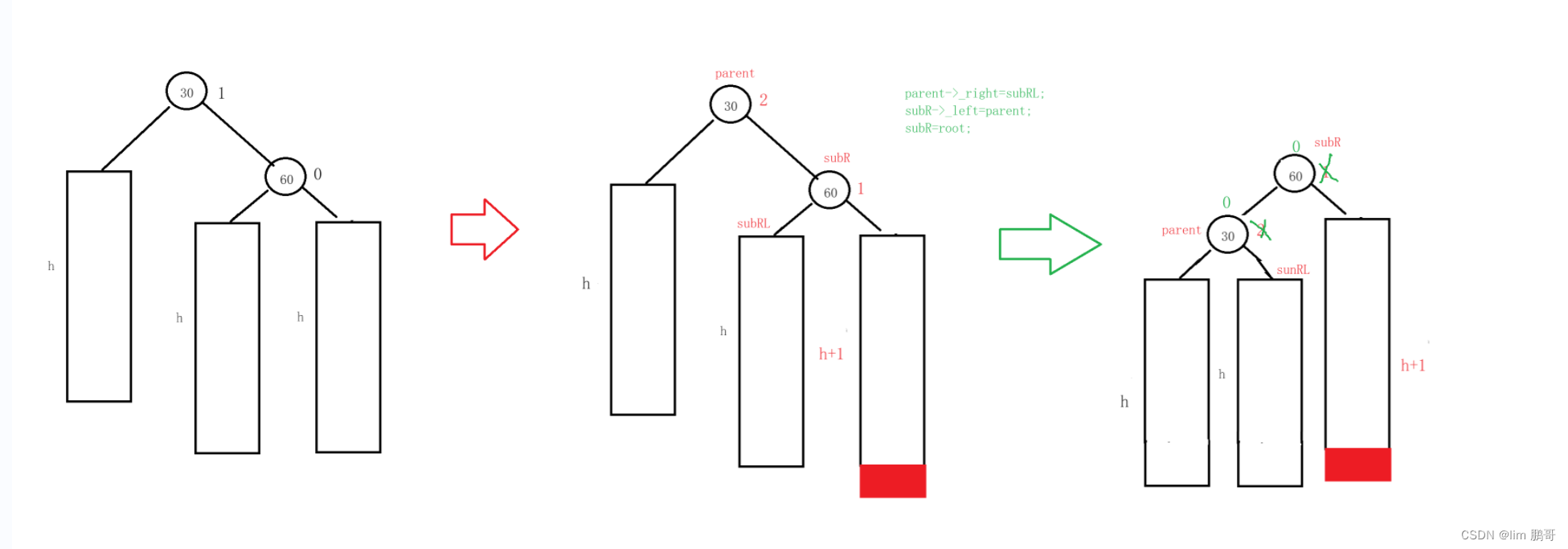
在这里插入图片描述

我们看看刚才将情况下的旋转
在这里插入图片描述

看一下代码实现

void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;//连接parent->_right = subRL;//subRL不一定存在if (subRL)subRL->_parent = parent;subR->_left = parent;//记录原来父节点的父亲，需要连接Node* ppnode = parent->_parent;parent->_parent = subR;//处理subR(当前根节点)if (parent == _root){_root = subR;subR->_parent = nullptr;}else{if (parent == ppnode->_left){ppnode->_left = subR;}else{ppnode->_right= subR;}subR->_parent = ppnode;}//更新平衡因子parent->_bf = 0;subR->_bf = 0;
}

右旋(cur->_bf = = -1 && parent->_bf == -2)

我们就直接画描述图了，不再一个个分析了
如果左子树的左边高我们需要进行右旋
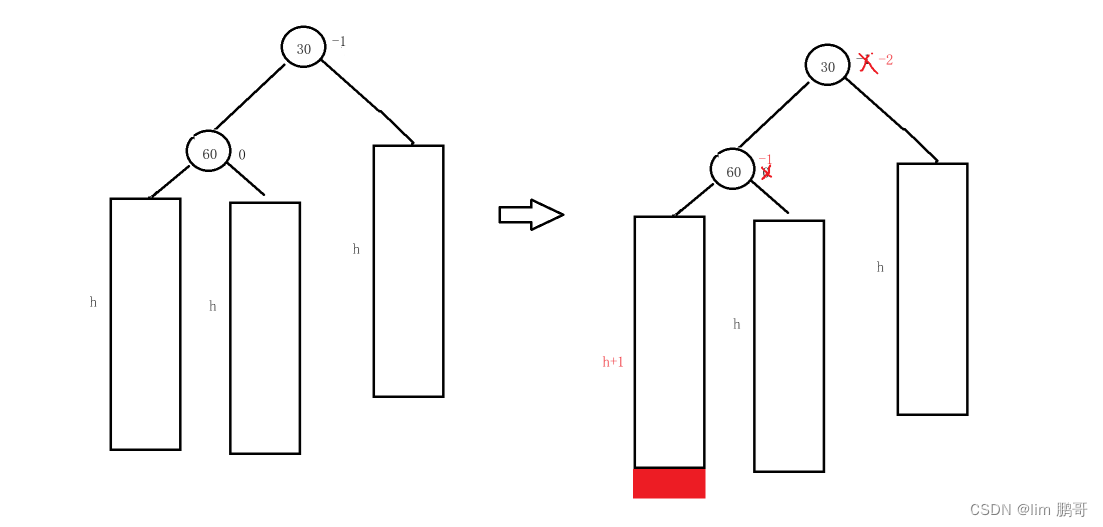
在这里插入图片描述

如何进行旋转呢？？

60的右子树作为30的左子树，30这棵树作为60的右子树，更新平衡因子
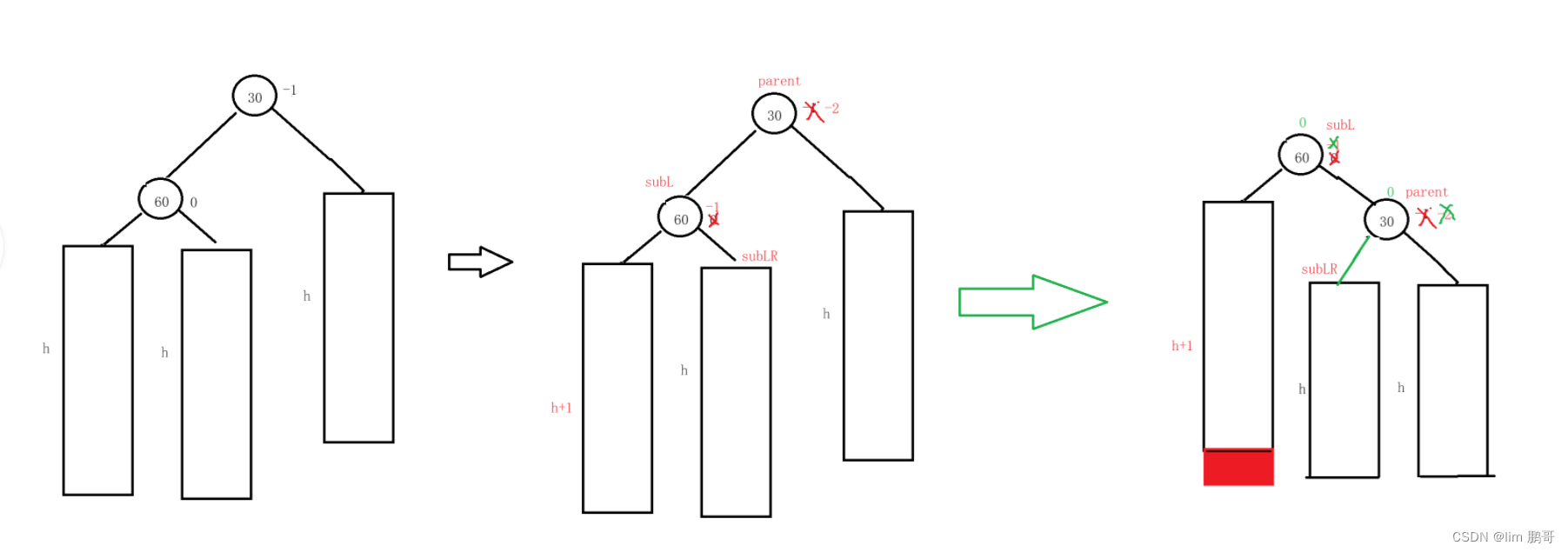
在这里插入图片描述

代码实现

void RotateR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;subL->_right = parent;//记录parent的父亲Node* ppnode = parent->_parent;parent->_parent = subL;if (parent == _root){_root = subL;_root->_parent = nullptr;}else{if (parent == ppnode->_left){ppnode->_left = subL;}else{ppnode->_right = subL;}subL->_parent = ppnode;}//更新平衡因子subL->_bf = 0;parent->_bf = 0;}

右左旋转 (cur->_bf = = -1 && parent->_bf == 2)

右子树的左边高

如果我们采用左旋的方式，不能完成要求

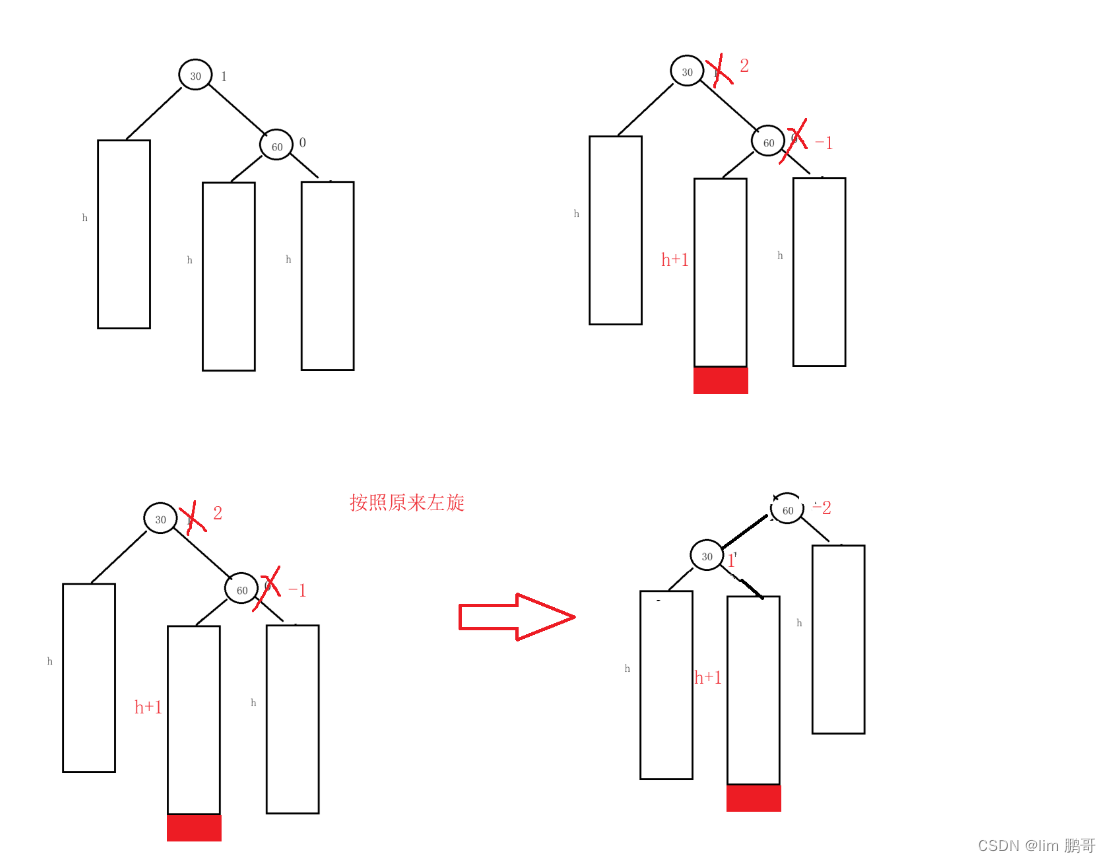
在这里插入图片描述

我们需要把这棵树进行拆分
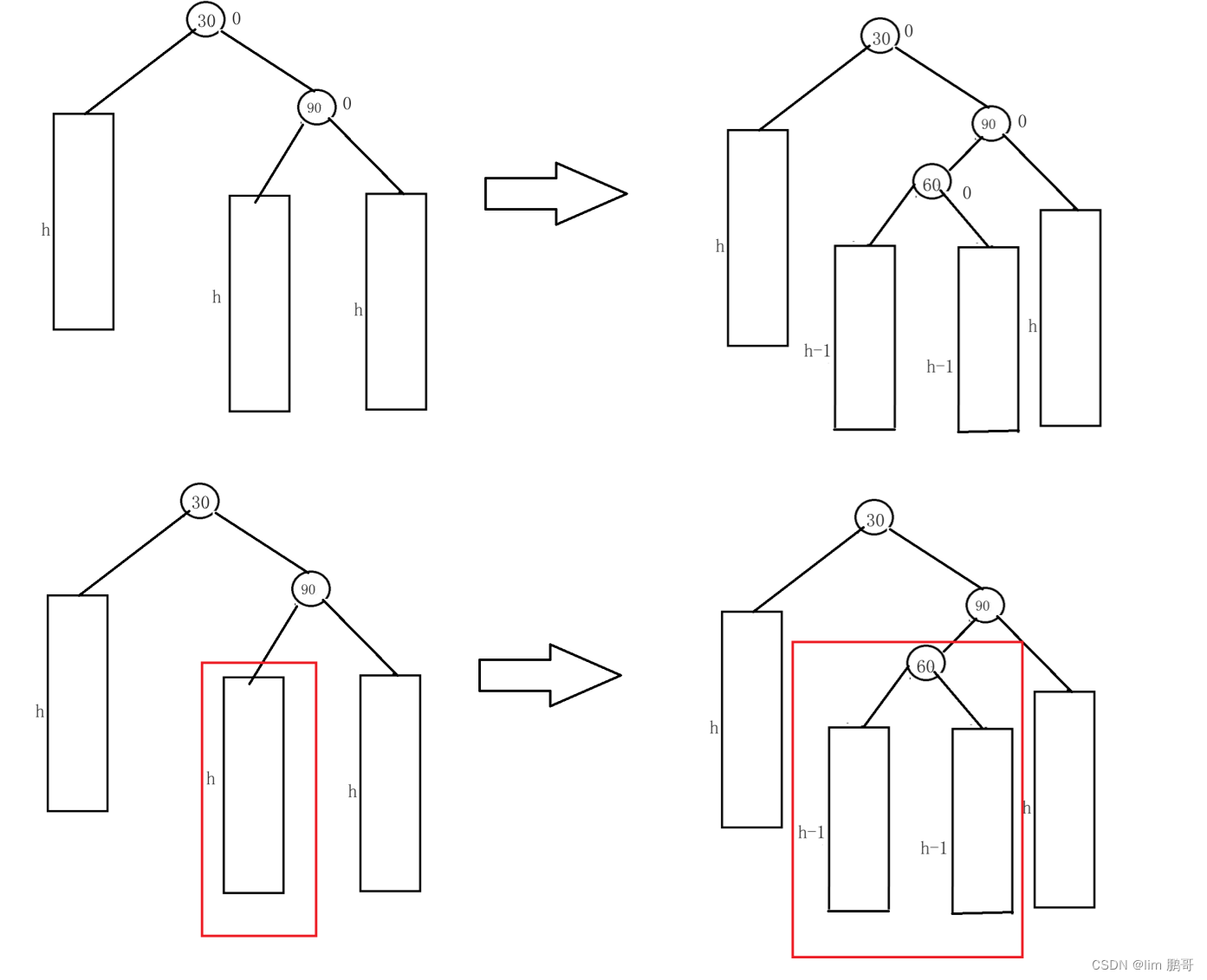
在这里插入图片描述

我们会分为三种情况(我们把这一块拆开来看待了)

✨60的左边插入
90先进行右旋，30进行左旋，更新平衡因子

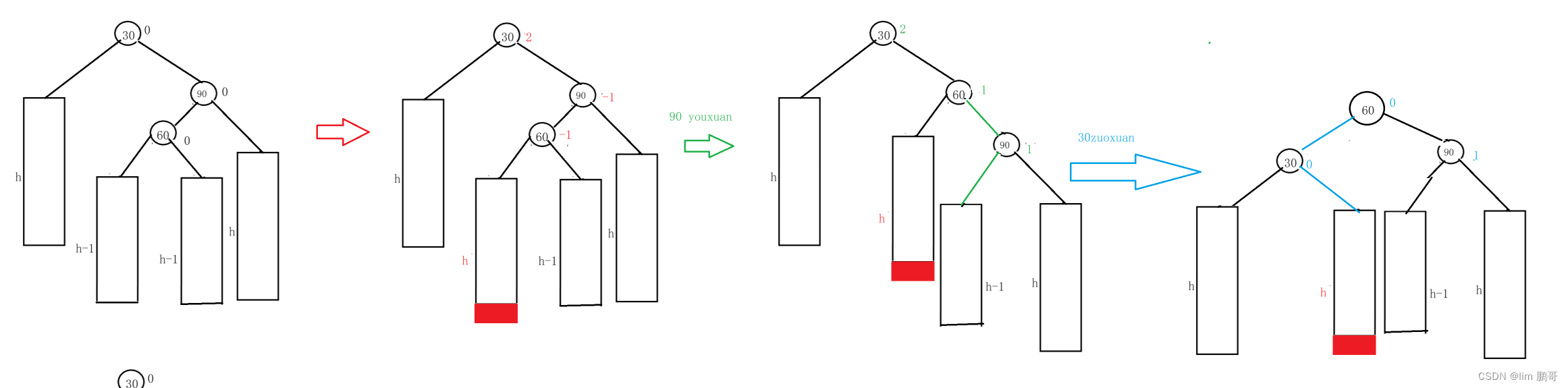
在这里插入图片描述

✨60的右边插入
90先进行右旋，30进行左旋，更新平衡因子
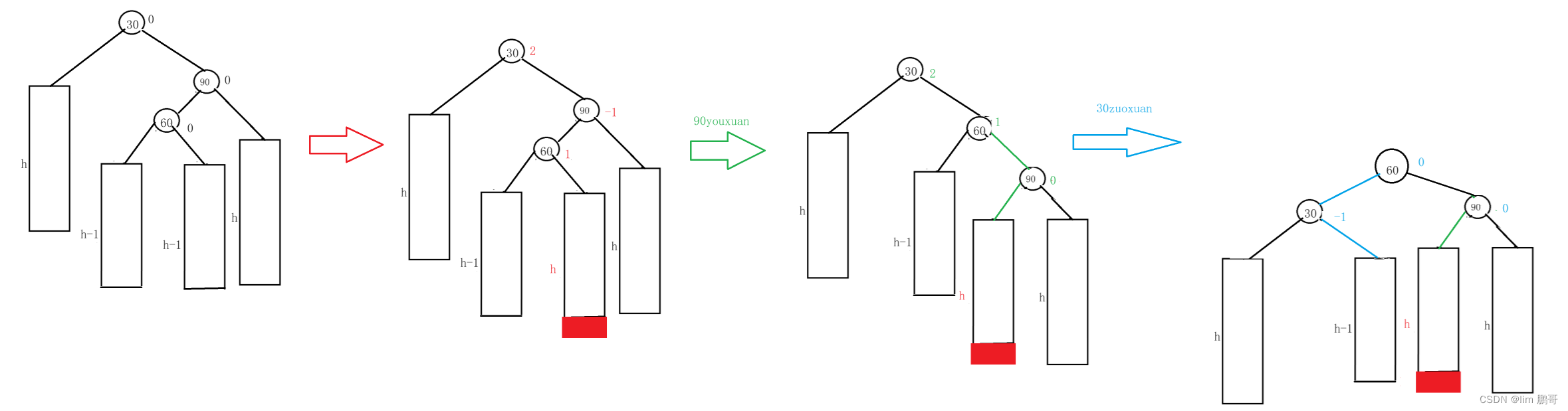
在这里插入图片描述

✨60就是插入节点
90先进行右旋，30进行左旋，更新平衡因子

在这里插入图片描述

我们这三种情况的最终的平衡因子都不相同，我们需要独立判断。
不同的根本原因就是插入位置的不同，也就是受60的影响。
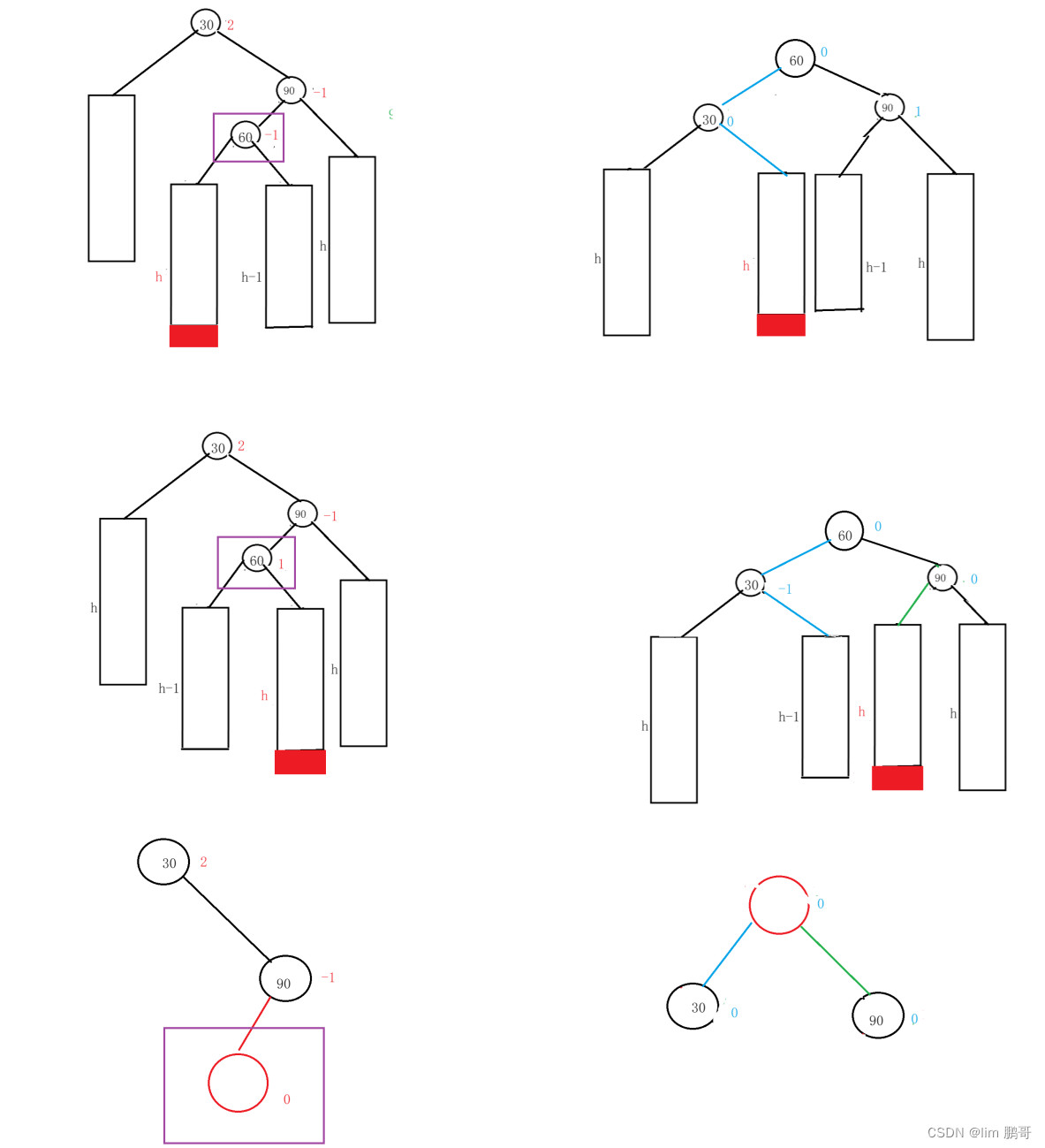
在这里插入图片描述

我们不关注过程，从上帝视觉来看一下
我们把60的左子树给了30的右子树，60的右子树给了90的左子树。把60推上去做根
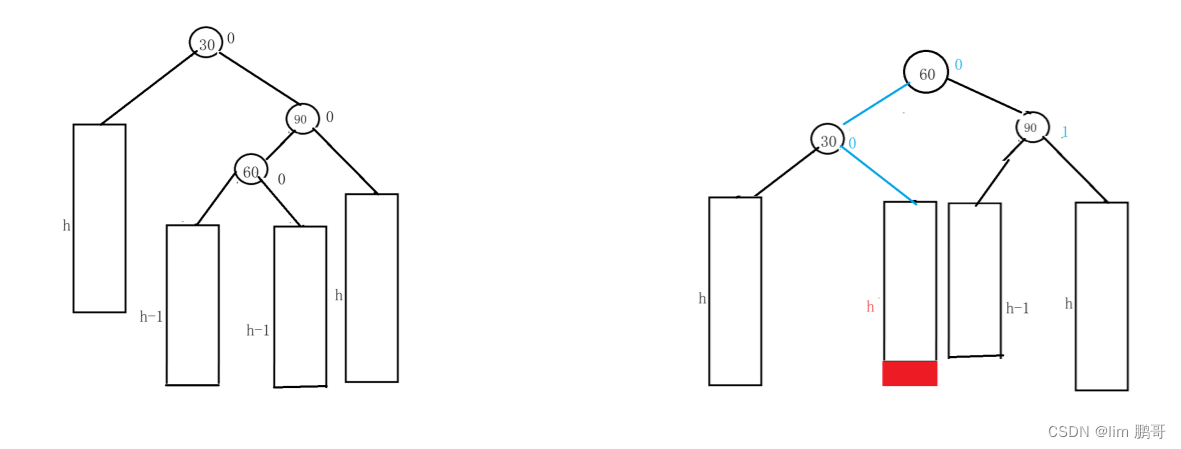
在这里插入图片描述

代码编写

void RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int usebf = subRL->_bf;//RotateR(subR);RotateL(parent);if (usebf == -1){parent->_bf = 0;subR->_bf = 1;subRL->_bf = 0;}else if (usebf == 1){parent->_bf = -1;subR->_bf = 0;subRL->_bf = 0;}else if (usebf == 0){parent->_bf = 0;subR->_bf = 0;subRL->_bf = 0;}else{assert(false);}
}

左右旋转 (cur->_bf = = 1 && parent->_bf == -2)

左子树的右边高
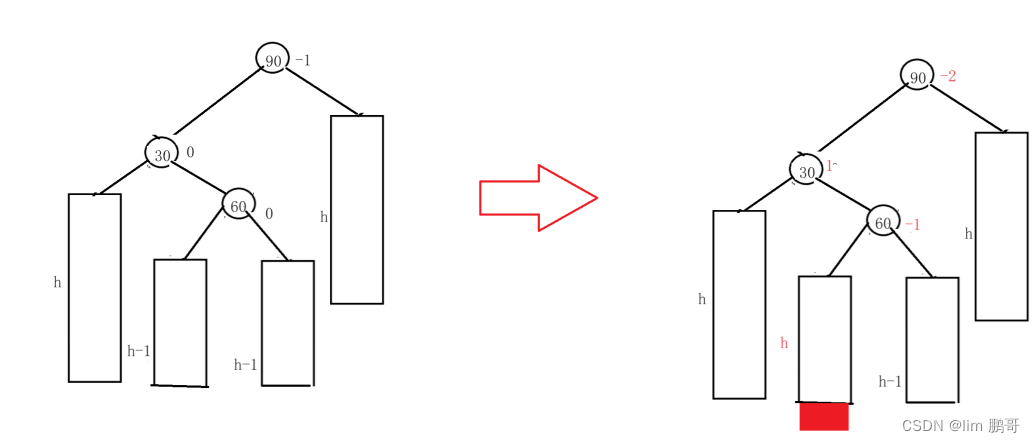
在这里插入图片描述

我们同样会分为三种情况
✨60的左边插入
先对30进行左旋，对90进行右旋，更新平衡因子

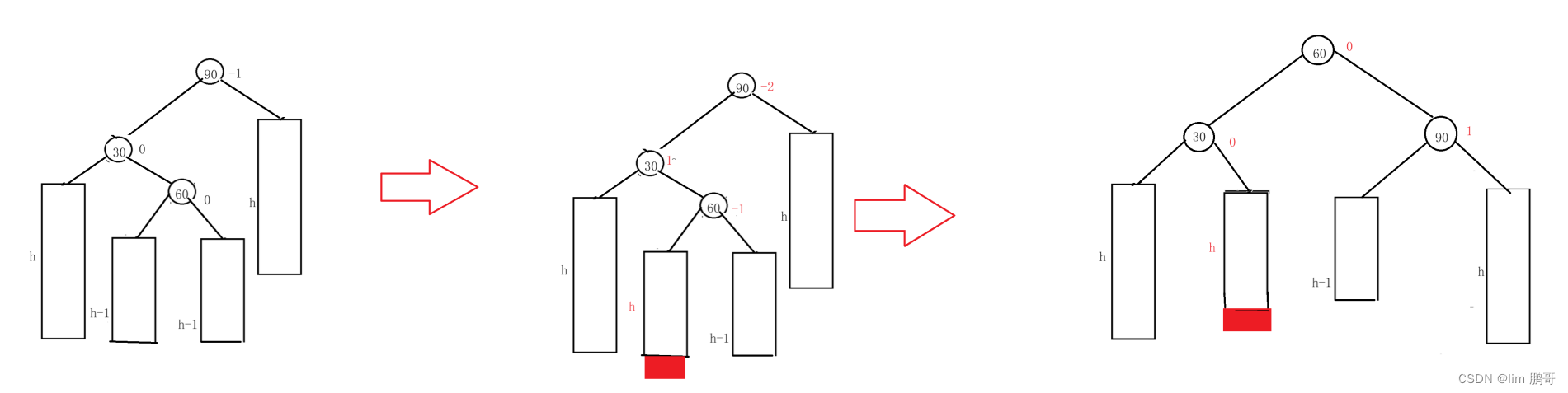
在这里插入图片描述
✨60的右边插入
先对30进行左旋，对90进行右旋，更新平衡因子

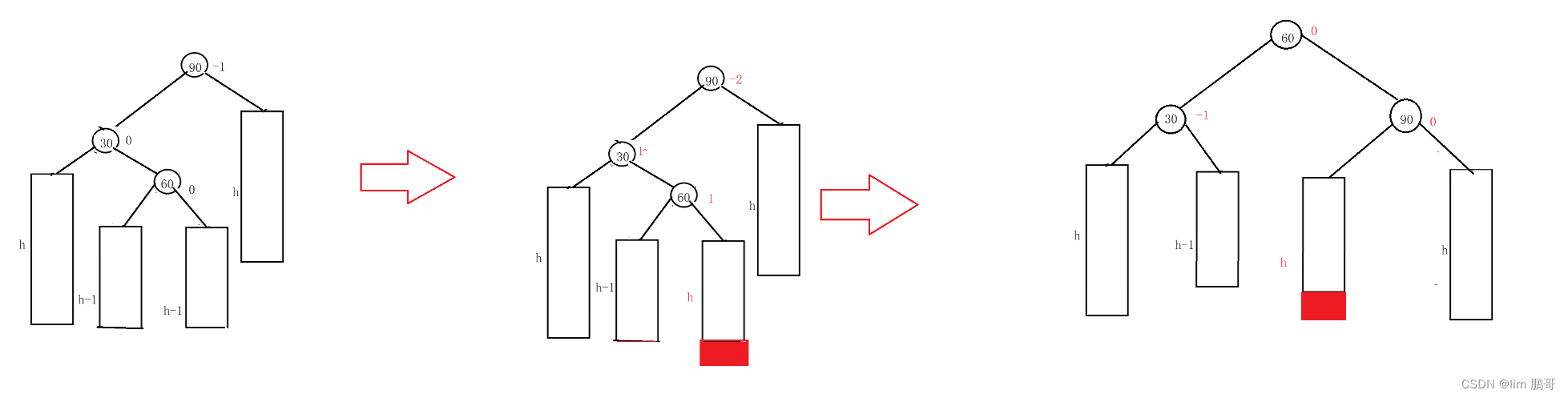
在这里插入图片描述

✨60就是插入节点
先对30进行左旋，对90进行右旋，更新平衡因子
此情况需要更新的平衡因子都是0.

代码编写

	void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int usebf = subLR->_bf;//RotateL(subL);RotateR(parent);if (usebf == -1){parent->_bf = 1;subL->_bf = 0;subLR->_bf = 0;}else if (usebf == 1){parent->_bf = 0;subL->_bf = -1;subLR->_bf = 0;}else if (usebf == 0){parent->_bf = 0;subL->_bf = 0;subLR->_bf = 0;}else{assert(false);}}

验证

我们如何验证这是一颗AVL树呢？？

AVL树同样具有二叉搜索树的特征，我们可以先中序遍历看看是否有序

	void Inorder(){_Inorder(_root);}void _Inorder(Node*root){if (root == nullptr){return;}_Inorder(root->_left);cout << root->_kv.first << " ";_Inorder(root->_right);}

但是我们仅仅通过中序遍历就能证明这是一颗AVL树吗？？？
这是句对不行的，AVL是一颗高度平衡二叉搜索树。
我们可以从高度入手，查看每一棵树高度是否满足为我们的需求。

	int Height(){return _Height(_root);}int _Height(Node* root){if (root == nullptr){return 0;}int LeftHeight = _Height(root->_left);int RightHeight = _Height(root->_right);return LeftHeight > RightHeight ? LeftHeight + 1 : RightHeight + 1;		}bool IsBalance(){return _IsBalance(_root);}bool _IsBalance(Node* root){if (root == nullptr){return true;}//左子树为真，右子树为真，根满足要求才能说明平衡if (_IsBalance(root->_left) == false){return false;}if (_IsBalance(root->_right) == false){return false;}int leftHeight = _Height(root->_left);int rightHeight= _Height(root->_right);if (abs(rightHeight - leftHeight)>2){cout << "不平衡" << endl;return false;}if (rightHeight - leftHeight != root->_bf){cout << "平衡因子异常" << endl;return false;}return true;}

我们通过验证，这个代码是没有任何问题的

我们来分析一下这段代码
以下面这棵树为例子进行分析。

我们写的是后序遍历，先判断0的左右子树，为true.
判断1时，需要重新求一下高度。
判断3时，需要重新求一下高度
判断5时，需要重新求一下高度

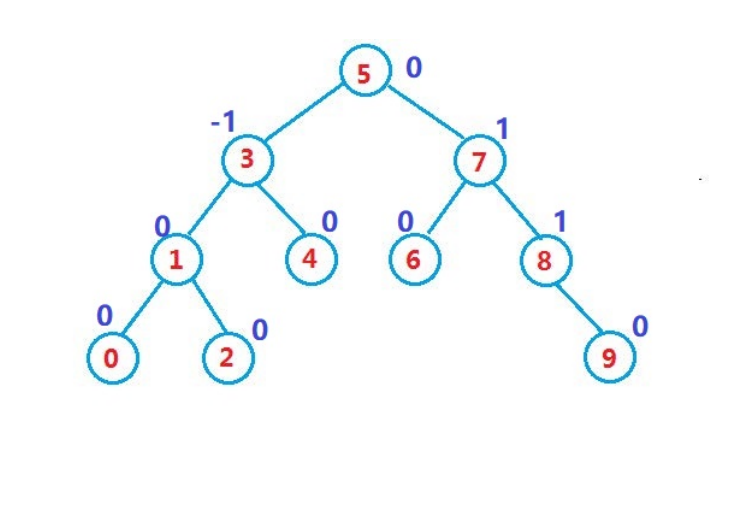
在这里插入图片描述

求高度就大量重复了，我们可不可以一边判断一边把高度带给上一层呢？？

bool IsBalance(){int height = 0;return _IsBalance(_root,height);}bool _IsBalance(Node*root,int &height){if (root == nullptr){height = 0;return true;}int leftHeight = 0;int rightHeight = 0;//左子树if (_IsBalance(root->_left, leftHeight)==false){return false;}//右子树if (_IsBalance(root->_right, rightHeight) == false){return false;}//根if (abs(rightHeight - leftHeight) > 2){cout << "不平衡" << endl;}if (rightHeight - leftHeight != root->_bf){cout << "平衡因子异常" << endl;}height = leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;return true;}

我们这段代码1就通过返回值的方式，将高度带给了上一层

验证用例
🌟常规场景1
{16, 3, 7, 11, 9, 26, 18, 14, 15}
🌟特殊场景2
{4, 2, 6, 1, 3, 5, 15, 7, 16, 14}
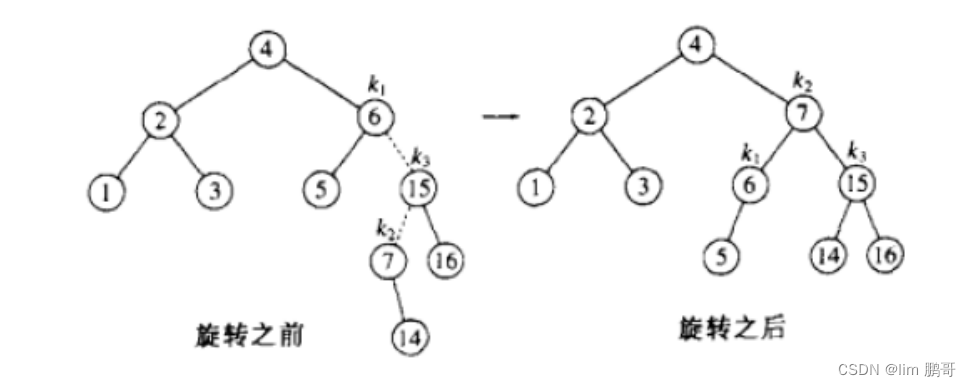
在这里插入图片描述

删除

删除是十分复杂的，我们在这里了就简单的讲述一下，不在进行模拟实现了。

删除和插入的总体逻辑没有太大出别
🌟根据二叉搜索树删除规则，查找到需要删除的节点
🌟更改平衡因子
🌟进行旋转
有兴趣的可以参考《算法导论》或《数据结构-用面向对象方法与C++描述》殷人昆版。

完整代码

#include <assert.h>
template<class K,class V>
struct AVLTreeNode
{AVLTreeNode(const pair<K,V>kv):_left(nullptr), _right(nullptr), _parent(nullptr),_kv(kv), _bf(0){ }AVLTreeNode<K, V> *_left;AVLTreeNode<K, V>*_right;AVLTreeNode<K, V>*_parent;pair<K, V>_kv;int _bf;//平衡因子
};template<class K,class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:AVLTree():_root(nullptr){}bool Insert(const pair<K, V>kv){//按照二叉搜索树规则插入if (_root == nullptr){_root = new Node(kv);return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_kv. first> kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(kv);cur->_parent = parent;if (kv.first > parent->_kv.first){parent->_right = cur;}else{parent->_left = cur;}//更新平衡因子//更新规则：右子树高度--左子树高度//更新到根节点结束while (parent){if (cur == parent->_left){parent->_bf--;}else{parent->_bf++;}//分三种情况if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}//进行旋转else if (parent->_bf == 2 || parent->_bf == -2){//左单旋if (cur->_bf == 1 && parent->_bf == 2){RotateL(parent);}//右单旋else if (cur->_bf == -1 && parent->_bf == -2){RotateR(parent);}//右左旋转else if (cur->_bf == -1 && parent->_bf == 2){RotateRL(parent);}//左右旋转else if (cur->_bf == 1 && parent->_bf == -2){RotateLR(parent);}else{assert(false);}//旋转之后结束break;}}return true;}void Inorder(){_Inorder(_root);}bool IsBalance(){int height = 0;return _IsBalance(_root,height);}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_kv.first < key){cur = cur->_right;}else if (cur->_kv.first > key){cur = cur->_left;}else{return cur;}}return NULL;}int Height(){return _Height(_root);}int Size(){return _Size(_root);}private:int _Height(Node* root){if (root == nullptr){return 0;}int LeftHeight = _Height(root->_left);int RightHeight = _Height(root->_right);return LeftHeight > RightHeight ? LeftHeight + 1 : RightHeight + 1;}int _Size(Node* root){if (root == nullptr){return 0;}int LeftSize = _Size(root->_left);int RightSize = _Size(root->_right);return LeftSize + RightSize + 1;}bool _IsBalance(Node*root,int &height){if (root == nullptr){height = 0;return true;}int leftHeight = 0;int rightHeight = 0;//左子树if (_IsBalance(root->_left, leftHeight)==false){return false;}//右子树if (_IsBalance(root->_right, rightHeight) == false){return false;}//根if (abs(rightHeight - leftHeight) > 2){cout << "不平衡" << endl;}if (rightHeight - leftHeight != root->_bf){cout << "平衡因子异常" << endl;}height = leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;return true;}void _Inorder(Node*root){if (root == nullptr){return;}_Inorder(root->_left);cout << root->_kv.first << " ";_Inorder(root->_right);}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;//连接parent->_right = subRL;//subRL不一定存在if (subRL)subRL->_parent = parent;subR->_left = parent;//记录原来父节点的父亲，需要连接Node* ppnode = parent->_parent;parent->_parent = subR;//处理subR(当前根节点)if (parent == _root){_root = subR;subR->_parent = nullptr;}else{if (parent == ppnode->_left){ppnode->_left = subR;}else{ppnode->_right= subR;}subR->_parent = ppnode;}//更新平衡因子parent->_bf = 0;subR->_bf = 0;}//右单旋void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;subL->_right = parent;//记录parent的父亲Node* ppnode = parent->_parent;parent->_parent = subL;if (parent == _root){_root = subL;_root->_parent = nullptr;}else{if (parent == ppnode->_left){ppnode->_left = subL;}else{ppnode->_right = subL;}subL->_parent = ppnode;}//更新平衡因子subL->_bf = 0;parent->_bf = 0;}void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int usebf = subRL->_bf;//RotateR(subR);RotateL(parent);if (usebf == -1){parent->_bf = 0;subR->_bf = 1;subRL->_bf = 0;}else if (usebf == 1){parent->_bf = -1;subR->_bf = 0;subRL->_bf = 0;}else if (usebf == 0){parent->_bf = 0;subR->_bf = 0;subRL->_bf = 0;}else{assert(false);}}void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int usebf = subLR->_bf;//RotateL(subL);RotateR(parent);if (usebf == -1){parent->_bf = 1;subL->_bf = 0;subLR->_bf = 0;}else if (usebf == 1){parent->_bf = 0;subL->_bf = -1;subLR->_bf = 0;}else if (usebf == 0){parent->_bf = 0;subL->_bf = 0;subLR->_bf = 0;}else{assert(false);}}Node* _root = nullptr;
};

性能分析

AVL是一颗绝对平衡的二叉搜索树，要求每个节点的左右子树高度差的绝对值不超过1，这样可以保证查询时，时间复杂度为O（logN）.
如果要对AVL树做一些结构修改的操作，性能非常低下。比如：插入时要维护绝对平衡，旋转次数比较多；删除时候，可能一直要调整到根位置。
如果需要一个查询高效且有序的数据结构，数据的个数为静态的（不变），可以考虑AVL；但是一个结构要经常修改，就不太合适。

我们可以通过下面代码测试一下


void TestAVLTree2()
{const int N = 10000000;vector<int> v;v.reserve(N);srand(time(0));for (size_t i = 0; i < N; i++){v.push_back(rand() + i);//cout << v.back() << endl;}size_t begin2 = clock();AVLTree<int, int> t;for (auto e : v){t.Insert(make_pair(e, e));//cout << "Insert:" << e << "->" << t.IsBalance() << endl;}size_t end2 = clock();cout << "Insert:" << end2 - begin2 << endl;cout << t.IsBalance() << endl;cout << "Height:" << t.Height() << endl;cout << "Size:" << t.Size() << endl;size_t begin1 = clock();// 确定在的值for (auto e : v){t.Find(e);}// 随机值//for (size_t i = 0; i < N; i++)//{//	t.Find((rand() + i));//}size_t end1 = clock();cout << "Find:" << end1 - begin1 << endl;
}

总结

以上就是今天要讲的内容，本文仅仅详细介绍了AVL树的一些特性，以及插入的左旋，右旋，双旋等操作，性能分析等等 。希望对大家的学习有所帮助，仅供参考 如有错误请大佬指点我会尽快去改正 欢迎大家来评论~~ 😘 😘 😘


http://www.ppmy.cn/ops/46271.html

相关文章

大泽动力高原柴油发电机参数型号

大泽动力高原柴油发电机参数型号

大泽动力高原柴油发电机是一款专为高原环境设计的柴油发电机&#xff0c;具备多项特点和优势。以下是关于大泽动力高原柴油发电机的详细介绍&#xff1a; 产品特点&#xff1a; 起动迅速&#xff1a;发电机起动时间只需几秒&#xff0c;能在短时间内达到全功率输出&#xff0c…
阅读更多...
Go 语言中的指针

Go 语言中的指针

在许多现代编程语言中&#xff0c;如 Java 和 .NET&#xff0c;程序员通常无法直接控制底层的内存管理。然而&#xff0c;Go 语言提供了这样的能力&#xff0c;同时限制了可能导致错误的操作&#xff0c;比如指针运算。 文章目录 1、Go 语言中指针的介绍1.1、什么是指针&#x…
阅读更多...
caxa新手怎么编程：一步步迈向精通的编程之旅

caxa新手怎么编程：一步步迈向精通的编程之旅

caxa新手怎么编程&#xff1a;一步步迈向精通的编程之旅 作为caxa的新手&#xff0c;想要快速入门并掌握编程技能&#xff0c;需要有一个系统的学习和实践过程。本文将从四个方面、五个方面、六个方面和七个方面&#xff0c;为你详细解读caxa编程的方法和技巧&#xff0c;帮助…
阅读更多...
MySQL之创建高性能的索引(十二)

MySQL之创建高性能的索引(十二)

创建高性能的索引 支持多种过滤条件 这些索引将满足大部分最常见的搜索查询&#xff0c;但是如何为一些生僻的搜索条件(比如has_pictures、eye_color、hair_colr和education)来设计索引呢&#xff1f;这些列的选择性搞&#xff0c;使用也不频繁&#xff0c;可以选择忽略它们&…
阅读更多...
C语言编程数学：探索、挑战与深度应用

C语言编程数学：探索、挑战与深度应用

C语言编程数学&#xff1a;探索、挑战与深度应用 C语言&#xff0c;作为计算机编程的基石之一&#xff0c;不仅广泛应用于系统级编程&#xff0c;还在数学计算领域发挥着重要作用。本文将围绕C语言在数学编程中的四个方面、五个方面、六个方面和七个方面展开探讨&#xff0c;带…
阅读更多...
如何恢复 Android 设备上丢失的照片

如何恢复 Android 设备上丢失的照片

由于我们的大量数据和日常生活都存储在一台设备上&#xff0c;因此有时将所有照片本地存储在 Android 智能手机或平板电脑上可能是一种冒险行为。无论是由于意外&#xff08;损坏、无意删除&#xff09;&#xff0c;还是您认识的人翻看您的设备并故意删除了您想要保留的照片&am…
阅读更多...
针对硅基氮化镓高电子迁移率晶体管(GaN-HEMT)的准物理等效电路模型，包含基板中射频漏电流的温度依赖性

针对硅基氮化镓高电子迁移率晶体管(GaN-HEMT)的准物理等效电路模型，包含基板中射频漏电流的温度依赖性

来源&#xff1a;Quasi-Physical Equivalent Circuit Model of RF Leakage Current in Substrate Including Temperature Dependence for GaN-HEMT on Si&#xff08;TMTT 23年&#xff09; 摘要 该文章提出了一种针对硅基氮化镓高电子迁移率晶体管&#xff08;GaN-HEMT&…
阅读更多...
MySQL性能分析工具——EXPLAIN

MySQL性能分析工具——EXPLAIN

性能分析工具——EXPLAIN 1、概述 定位了查询慢的SQL之后&#xff0c;我们就可以使用EXPLAIN或DESCRIBE工具做针对性的分析查询语句 。 DESCRIBE语句的使用方法与EXPLAIN语句是一样的&#xff0c;并且分析结果也是一样的。 MySQL中有专门负责优化SELECT语句的优化器模块&…
阅读更多...
最新文章

Copyright @ 2022~2023