【算法】基础算法004之前缀和

👀樊梓慕：个人主页

🎥个人专栏：《C语言》《数据结构》《蓝桥杯试题》《LeetCode刷题笔记》《实训项目》《C++》《Linux》《算法》

🌝每一个不曾起舞的日子，都是对生命的辜负

前言

本篇文章为大家带来前缀和算法，前缀和算法可以以O(1)的时间复杂度快速求出某一段连续区间的和，这个连续区域既可以是一维的也可以是二维的。

欢迎大家📂收藏📂以便未来做题时可以快速找到思路，巧妙的方法可以事半功倍。

=========================================================================

GITEE相关代码：🌟樊飞 (fanfei_c) - Gitee.com🌟

=========================================================================

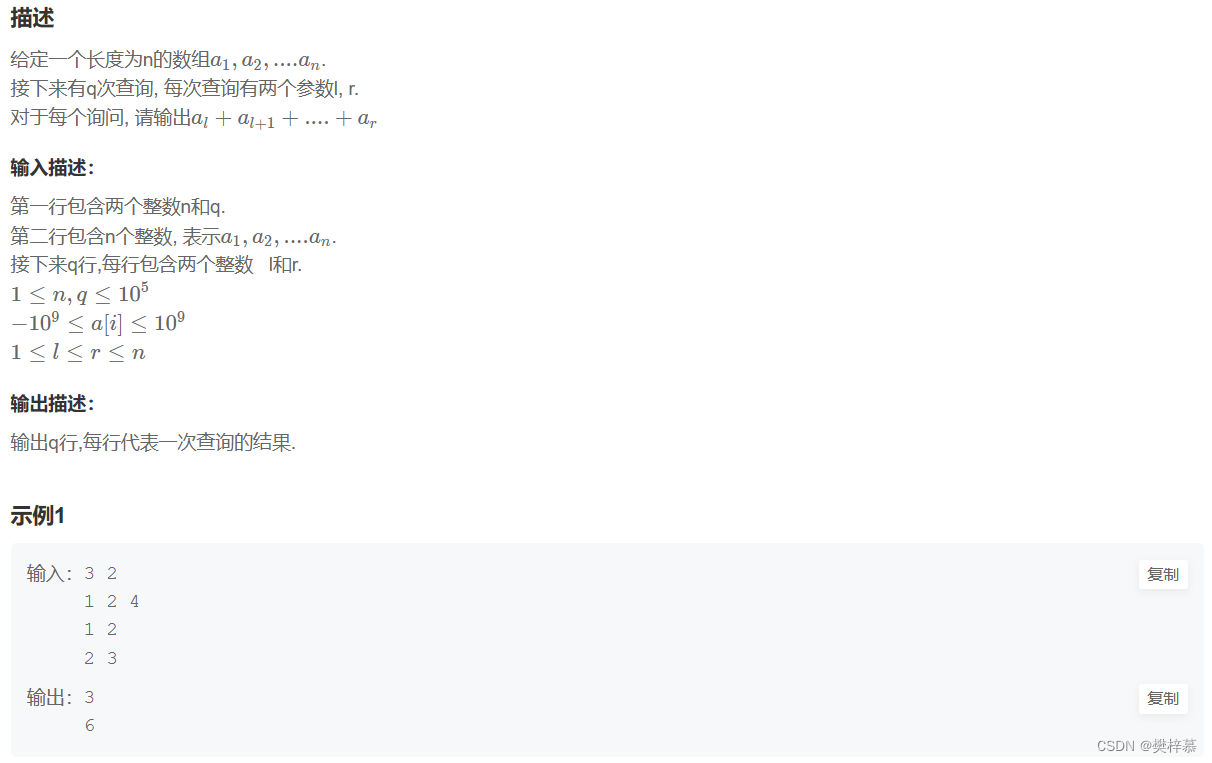
1.⼀维前缀和

【模板】前缀和_牛客题霸_牛客网 (nowcoder.com)https://www.nowcoder.com/practice/acead2f4c28c401889915da98ecdc6bf?tpId=230&tqId=2021480&ru=/exam/oj&qru=/ta/dynamic-programming/question-ranking&sourceUrl=%2Fexam%2Foj%3Fpage%3D1%26tab%3D%25E7%25AE%2597%25E6%25B3%2595%25E7%25AF%2587%26topicId%3D196

前缀和：可以快速求出某一段连续区间的和。

本道题目如果使用暴力计算的话会超时，所以需要进行优化。

前缀和解题模板

第一步：预处理出来一个前缀和数组，比如本题dp[i]表示1-i区间内所有元素的和，且dp[i]=dp[i-1]+arr[i]；
第二步：使用前缀和数组，比如本题求[l,r]区间元素的和就是dp[r]-dp[l-1]；

#include <iostream>
#include <vector>
using namespace std;int main() {// 1.输入数据int n,q;cin>>n>>q;vector<int> arr(n+1);for(int i=1;i<=n;i++) cin>>arr[i];// 2.预处理出来一个前缀和数组vector<long long> dp(n+1);for(int i=1;i<=n;i++) dp[i]=dp[i-1]+arr[i]; // 3.使用前缀和数组int l,r;while(q--){cin>>l>>r;cout<<dp[r]-dp[l-1]<<endl;}return 0;
}

注意：

防止溢出，所以dp数据类型选用long long；
多开一个空间（n+1）是为了防止越界，因为最后需要[l-1]，所以下标一般都是以1为起始。

2.二维前缀和

【模板】二维前缀和_牛客题霸_牛客网 (nowcoder.com)https://www.nowcoder.com/practice/99eb8040d116414ea3296467ce81cbbc?tpId=230&tqId=2023819&ru=/exam/oj&qru=/ta/dynamic-programming/question-ranking&sourceUrl=%2Fexam%2Foj%3Fpage%3D1%26tab%3D%25E7%25AE%2597%25E6%25B3%2595%25E7%25AF%2587%26topicId%3D196

同样的我们使用前缀和解题模板：

第一步：预处理出来一个前缀和数组，本题中dp[i][j]表示[1,1]-[i][j]区间内所有元素的和。
第二步：使用前缀和数组。

首先如何得到状态转移方程，即dp[i][j]如何计算？

如图所示：

很明显dp[i][j]=A+B+C+D。

但是A还好说，B和C都不好计算。

那么我们就可以把A、B合并为A+B=dp[i-1][j]，把A、C合并为A+C=dp[i][j-1]。

多加了一个A再减去即可。

所以dp[i][j]=(A+B)+(A+C)+D-A=dp[i-1][j]+dp[i][j-1]+arr[i][j]-dp[i-1][j-1]；

其次如何使用前缀和数组？

同样如上图，[x1][y1]~[x2][y2]的和我们用D块表示。

那么D=A+B+C+D-(A+B)-(A+C)+A=dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1]；

#include <iostream>
#include <vector>
using namespace std;int main() {// 1.输入数据int n,m,q;cin>>n>>m>>q;vector<vector<int>> arr(n+1,vector<int>(m+1));for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)cin>>arr[i][j];// 2.预处理前缀和矩阵vector<vector<long long>> dp(n+1,vector<long long>(m+1));for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){dp[i][j]=dp[i-1][j]+dp[i][j-1]+arr[i][j]-dp[i-1][j-1];}}// 3.使用前缀和矩阵int x1,y1,x2,y2;while(q--){cin>>x1>>y1>>x2>>y2;cout<<dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1]<<endl;}return 0;
}

3.练习

724. 寻找数组的中心下标 - 力扣（LeetCode）https://leetcode.cn/problems/find-pivot-index/238. 除自身以外数组的乘积 - 力扣（LeetCode）https://leetcode.cn/problems/product-of-array-except-self/560. 和为 K 的子数组 - 力扣（LeetCode）https://leetcode.cn/problems/subarray-sum-equals-k/

提示：前缀和+哈希表

974. 和可被 K 整除的子数组 - 力扣（LeetCode）https://leetcode.cn/problems/subarray-sums-divisible-by-k/description/

补充知识以及思路提示：

1.同余定理

若（a-b）/ p = k ···· 0； //可以整除

则 a % p = b % p；

对于本题来说，我们需要找到可以被k整除的子数组，那么我们假设这段子数组是以i为结尾，x为起始的，整个数组的和为sum，x的前缀和为pre，那么有(sum-pre)%k=0，又因为同余定理可以得到sum%k=pre%k，所以我们只需要将sum%k的结果添加到哈希表中，最后统计哈希表中该余数出现的次数即可，根据后面给出的修正方法，这里求余公式变为（sum%k+k）%k。

2.C++、java对负数 % 正数的结果以及修正

在C++和java语言中负数%正数的结果是一个负数，那么为了让这个负数修正为正数，我们可以利用如下公式：

a为负数，b为正数，那么修正后的余数 = a % b + b，而为了同一处理正负数，我们可以再对这个结果取模，目的是当a为正数时，也不越界。

所以修正后的余数 = （a%b+b）% b；

525. 连续数组 - 力扣（LeetCode）https://leetcode.cn/problems/contiguous-array/

思路提示：

本题让我们找出⼀段连续的区间， 0 和 1 出现的次数相同。
• 如果将 0 记为 -1 ， 1 记为 1 ，问题就变成了找出一段区间，这段区间的和等于 0 。
• 于是，就和『和为K的子数组』这道题的思路一样了，只不过K的值变为0；

1314. 矩阵区域和 - 力扣（LeetCode）https://leetcode.cn/problems/matrix-block-sum/

提示：二维前缀和思路

=========================================================================

如果你对该系列文章有兴趣的话，欢迎持续关注博主动态，博主会持续输出优质内容

🍎博主很需要大家的支持，你的支持是我创作的不竭动力🍎

🌟~ 点赞收藏＋关注 ~🌟

=========================================================================