TikTok 喘息
继上月通过强制剥离 TikTok 法案后,美国众议院在当地时间 20 日下午以 360 票赞成 58 票反对通过了新的法案:剥离 TikTok 的期限由生效后 165 天调整至 270 天之内,即今年 11 月的美国总统大选后。
之前我们讲过,TikTok 比较好的破局方式,只能是期望当时躲过特朗普狙击的方法能再奏效一次,发动用户把动静搞大,尽量拖延法案通过的日期,目的是将禁令实施拖到大选之后。
目前看来,这一步现在已经达到,但这不意味 TikTok 走出困局。
在这个窗口期中,TikTok 一方面能做的是稳住根基。自从上月颁布禁令之后,不少中大企业开始逐步将业务搬离 TikTok,这显然会让美国公司利益和 TikTok 存亡进行松绑,TikTok 应当尽最大的努力留着这些公司;另一方面是继续维护好舆论场中的受害方形象,确保禁令话题的在美热度,持续发动用户对国会制造麻烦,目前除了 TikTok 用户,以及一众网红公开力挺 TikTok 以外,连 X(前推特)的老板马斯克也表示 TikTok 不该被禁,禁令有悖于言论和表达自由。
当然,也要做好最坏的打算,即「退出美国」的准备。
卖是不可能卖的,这背后原因远不是公司所属权这么简单。
...
回归主线。
来一道和「字节跳动」相关的算法原题。
题目描述
平台:LeetCode
题号:1210
你还记得那条风靡全球的贪吃蛇吗?
我们在一个 n*n 的网格上构建了新的迷宫地图,蛇的长度为 2,也就是说它会占去两个单元格。蛇会从左上角((0, 0) 和 (0, 1))开始移动。我们用 0 表示空单元格,用 1 表示障碍物。
蛇需要移动到迷宫的右下角((n-1, n-2) 和 (n-1, n-1))。
每次移动,蛇可以这样走:
-
如果没有障碍,则向右移动一个单元格。并仍然保持身体的水平/竖直状态。 -
如果没有障碍,则向下移动一个单元格。并仍然保持身体的水平/竖直状态。 -
如果它处于水平状态并且其下面的两个单元都是空的,就顺时针旋转 90度。蛇从((r, c)、(r, c+1))移动到 ((r, c)、(r+1, c))。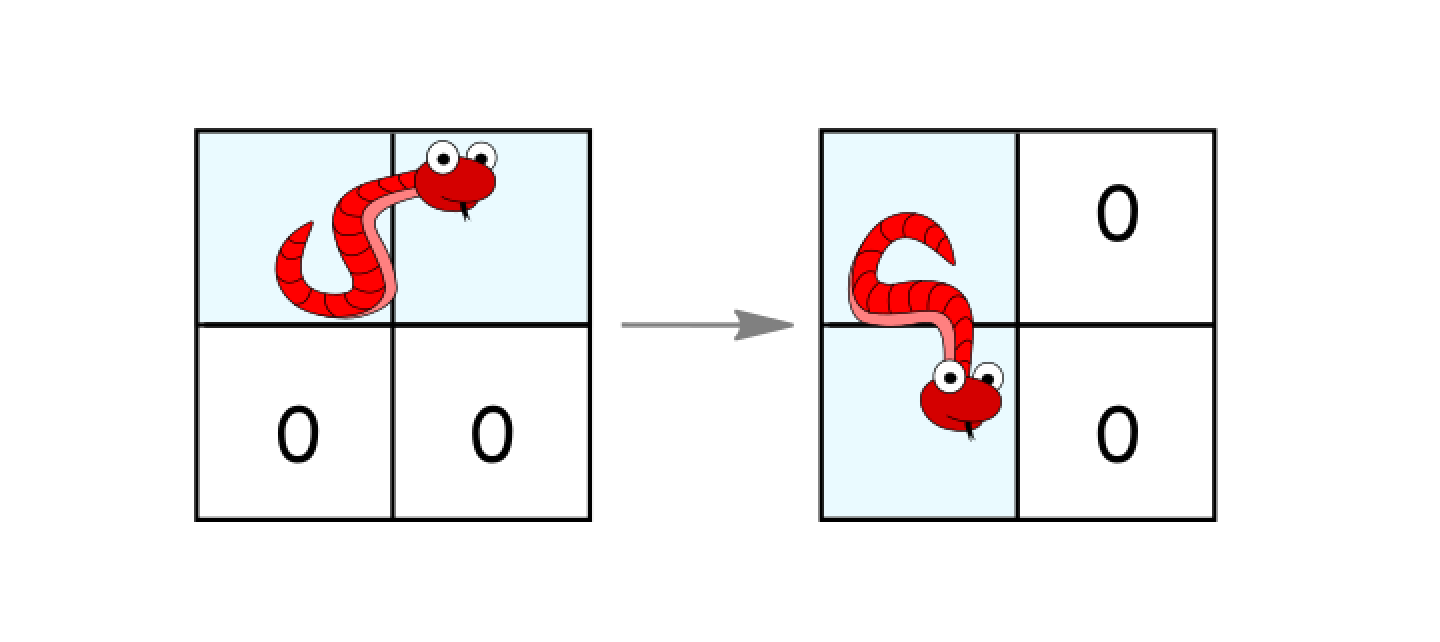
-
如果它处于竖直状态并且其右面的两个单元都是空的,就逆时针旋转 90度。蛇从((r, c)、(r+1, c))移动到((r, c)、(r, c+1))。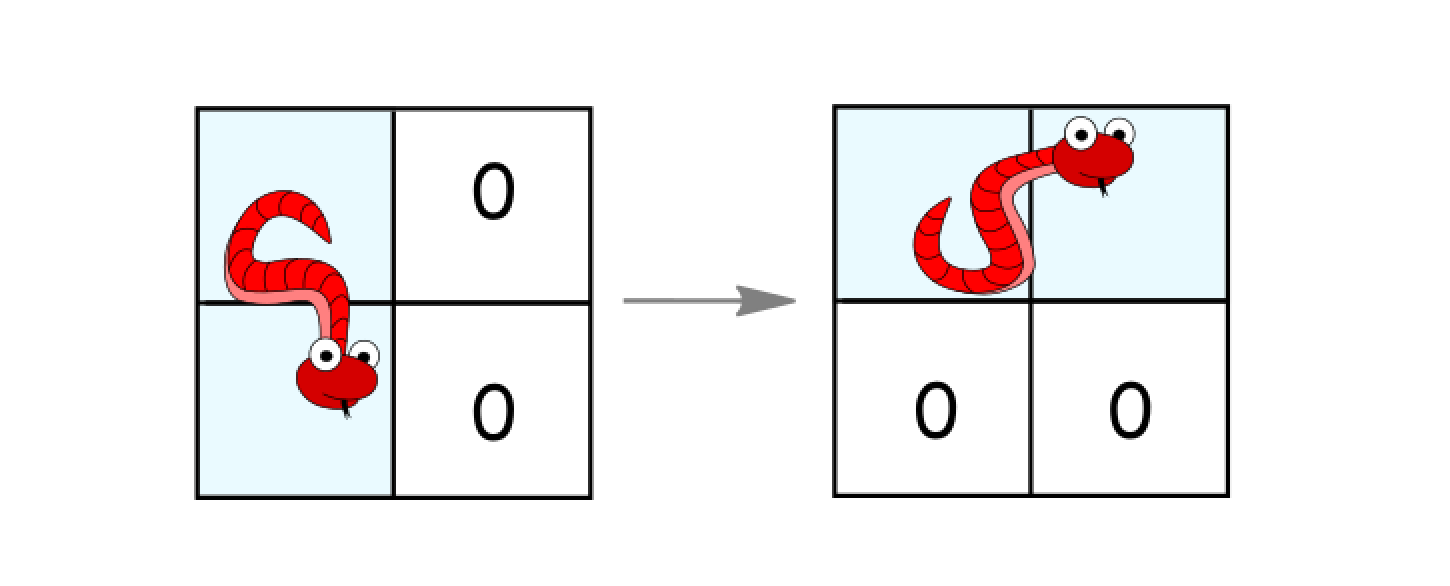
返回蛇抵达目的地所需的最少移动次数。
如果无法到达目的地,请返回 -1。
示例 1: 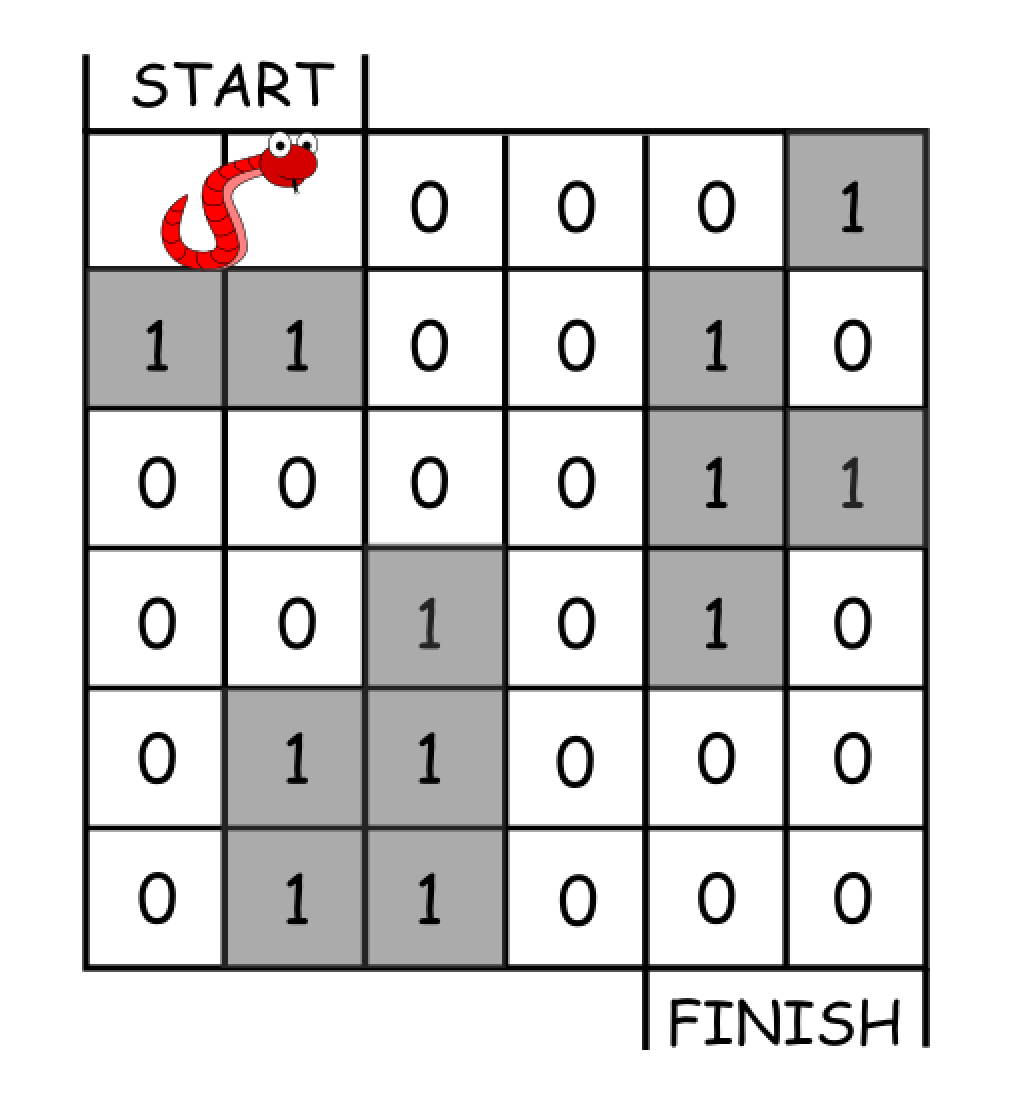
输入:grid = [[0,0,0,0,0,1],
[1,1,0,0,1,0],
[0,0,0,0,1,1],
[0,0,1,0,1,0],
[0,1,1,0,0,0],
[0,1,1,0,0,0]]
输出:11
解释:
一种可能的解决方案是 [右, 右, 顺时针旋转, 右, 下, 下, 下, 下, 逆时针旋转, 右, 下]。
示例 2:
输入:grid = [[0,0,1,1,1,1],
[0,0,0,0,1,1],
[1,1,0,0,0,1],
[1,1,1,0,0,1],
[1,1,1,0,0,1],
[1,1,1,0,0,0]]
输出:9
提示:
-
-
-
蛇保证从空单元格开始出发。
BFS
题目要我们求从特定起点到特定终点的最少步数,由于我们蛇的长度固定为 ,因此我们可用三元组 来代表蛇的实际位置。其中 代表蛇尾位置, 代表当前蛇的方向状态, 代表水平状态, 代表竖直状态。
蛇尾加上方向状态可确定其蛇头位置 :tx = cd == 0 ? nx : nx + 1、ty = cd == 0 ? ny + 1 : ny。
对四种移动规则所导致三元组变化进行分情况讨论:
-
往右移动:对于蛇尾而言,只有维度 进行加一,其余维度不变。三元组变化总结为 -
往下移动:对于蛇尾而言,只有维度 进行加一,其余维度不变。三元组变化总结为 -
旋转:对于蛇尾,只有 维度对进行翻转,其余维度不变。三元组变化总结定为
综上,所有移动规则可总结为 int[][] dirs = new int[][]{{1,0,0},{0,1,0},{0,0,1}}。
在进行 BFS 时,通过遍历 dirs 来得到新的三元组:原位置 (x, y, cd) 转换到新位置 (x + dir[0], y + dir[1], cd ^ dir[2])。
在得到新蛇尾位置 之后,计算新蛇头的位置 。需要确保整条蛇没有越界,没有碰到障碍物,并且旋转转移时,额外检查 位置是否合法。
Java 代码:
class Solution {
int[][] dirs = new int[][]{{1,0,0},{0,1,0},{0,0,1}};
public int minimumMoves(int[][] g) {
int n = g.length;
Deque<int[]> d = new ArrayDeque<>();
d.addLast(new int[]{0,0,0,0});
boolean[][][] vis = new boolean[n][n][2];
vis[0][0][0] = true;
while (!d.isEmpty()) {
int[] info = d.pollFirst();
int x = info[0], y = info[1], cd = info[2], step = info[3];
for (int[] dir : dirs) {
int nx = x + dir[0], ny = y + dir[1], nd = cd ^ dir[2]; // 新蛇尾位置和方向
int tx = nd == 0 ? nx : nx + 1, ty = nd == 0 ? ny + 1 : ny; // 新蛇头
if (nx >= n || ny >= n || tx >= n || ty >= n) continue; // 整条蛇不越界
if (g[nx][ny] == 1 || g[tx][ty] == 1) continue; // 没有触及障碍物
if (vis[nx][ny][nd]) continue;
if (cd != nd && g[x + 1][y + 1] == 1) continue; // 旋转时,额外检查多一个位置
if (nx == n - 1 && ny == n - 2 && nd == 0) return step + 1;
d.addLast(new int[]{nx, ny, nd, step + 1});
vis[nx][ny][nd] = true;
}
}
return -1;
}
}
C++ 代码:
class Solution {
public:
int minimumMoves(vector<vector<int>>& g) {
vector<vector<int>> dirs = {{1,0,0}, {0,1,0}, {0,0,1}};
int n = g.size();
queue<vector<int>> d;
d.push({0, 0, 0, 0});
vector<vector<vector<bool>>> vis(n, vector<vector<bool>>(n, vector<bool>(2, false)));
vis[0][0][0] = true;
while (!d.empty()) {
vector<int> info = d.front();
d.pop();
int x = info[0], y = info[1], cd = info[2], step = info[3];
for (vector<int>& dir : dirs) {
int nx = x + dir[0], ny = y + dir[1], nd = cd ^ dir[2];
int tx = nd == 0 ? nx : nx + 1, ty = nd == 0 ? ny + 1 : ny;
if (nx >= n || ny >= n || tx >= n || ty >= n) continue;
if (g[nx][ny] == 1 || g[tx][ty] == 1) continue;
if (vis[nx][ny][nd]) continue;
if (cd != nd && g[x + 1][y + 1] == 1) continue;
if (nx == n - 1 && ny == n - 2 && nd == 0) return step + 1;
d.push({nx, ny, nd, step + 1});
vis[nx][ny][nd] = true;
}
}
return -1;
}
};
Python 代码:
class Solution:
def minimumMoves(self, g: List[List[int]]) -> int:
dirs = [(1, 0, 0), (0, 1, 0), (0, 0, 1)]
n = len(g)
d = deque([(0,0,0,0)])
vis = [[[0]*2 for _ in range(n)] for _ in range(n)]
vis[0][0][0] = 1
while d:
x, y, cd, step = d.popleft()
for dir in dirs:
nx, ny, nd = x + dir[0], y + dir[1], cd ^ dir[2]
tx, ty = nx + (nd == 1), ny + (nd == 0)
if nx >= n or ny >= n or tx >= n or ty >= n: continue
if g[nx][ny] == 1 or g[tx][ty] == 1: continue
if vis[nx][ny][nd]: continue
if cd != nd and g[x + 1][y + 1] == 1: continue
if nx == n - 1 and ny == n - 2 and nd == 0: return step + 1
d.append((nx, ny, nd, step + 1))
vis[nx][ny][nd] = 1
return -1
TypeScript 代码:
function minimumMoves(g: number[][]): number {
const n = g.length;
const d: [number, number, number, number][] = [[0,0,0,0]];
const vis: boolean[][][] = Array.from({ length: n }, () => Array.from({ length: n }, () => [false, false]));
vis[0][0][0] = true;
const dirs: [number, number, number][] = [[1,0,0], [0,1,0], [0,0,1]];
while (d.length > 0) {
const [x, y, cd, step] = d.shift()!;
for (const dir of dirs) {
const nx = x + dir[0], ny = y + dir[1], nd = cd ^ dir[2];
const tx = nd === 0 ? nx : nx + 1, ty = nd === 0 ? ny + 1 : ny;
if (nx >= n || ny >= n || tx >= n || ty >= n) continue;
if (g[nx][ny] === 1 || g[tx][ty] === 1) continue
if (vis[nx][ny][nd]) continue;
if (cd !== nd && g[x + 1][y + 1] === 1) continue;
if (nx === n - 1 && ny === n - 2 && nd === 0) return step + 1;
d.push([nx, ny, nd, step + 1]);
vis[nx][ny][nd] = true;
}
}
return -1;
};
-
时间复杂度: -
空间复杂度: ,其中 代表蛇可变状态方向
最后
给大伙通知一下 📢 :
全网最低价 LeetCode 会员目前仍可用!!!
📅 年度会员:有效期加赠两个月!!; 季度会员:有效期加赠两周!!
🧧 年度会员:获 66.66 现金红包!!; 季度会员:获 22.22 现金红包!!
🎁 年度会员:参与当月丰厚专属实物抽奖(中奖率 > 30%)!!
专属链接:leetcode.cn/premium/?promoChannel=acoier
我是宫水三叶,每天都会分享算法知识,并和大家聊聊近期的所见所闻。
欢迎关注,明天见。
更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地 🎉🎉