【1】引言
前序学习进程中,我们至少掌握了两种方法,可以实现对图像实现缩放。
第一种方法是调用cv2.resize()函数实现,相关学习链接为:
python学opencv|读取图像(三)放大和缩小图像_python opencv 读取图片缩放-CSDN博客
第二种方法是在cv2.getRotationMatrix2D()函数旋转缩放图像时,顺带实现了图像缩放:
python学opencv|读取图像(二十八)使用cv2.getRotationMatrix2D()函数旋转缩放图像-CSDN博客
实际上,对于第二种方法,如果我们只设置旋转角度=0,其实就是只对图像进行放大和缩小。为验证这个猜想,我们可以做测试。
【2】前两种方法代码测试
【2.1】cv2.getRotationMatrix2D()函数缩放
首先我们给出完整代码:
python">import cv2 as cv # 引入CV模块
import numpy as np #引入numpy模块# 读取图片
src = cv.imread('src.png')
rows=len(src) #读取图像行数
cols=len(src[0]) #读取图像列数
center=(rows/2,cols/2) #旋转中心
#M=np.float32([[1,0,50],#[0,1,200]]) #M矩阵,x=50,y=200
M=cv.getRotationMatrix2D(center,0,0.8) #旋转并缩放图像
dst=cv.warpAffine(src,M,(cols,rows)) #输出图像
cv.imshow('src-pingyi', dst) # 在屏幕展示绘制圆形的效果
cv.imwrite('src-suofang.png', dst) # 保存图像
cv.waitKey() # 图像不会自动关闭
cv.destroyAllWindows() # 释放所有窗口
其中对于函数的设置,把旋转角度设定为0,缩放倍数为0.8:
M=cv.getRotationMatrix2D(center,0,0.8) #旋转并缩放图像
使用的原始图像为:

图1 src.png
缩放后的图像为:

图2 缩小0.8倍后的图像
如果我们把缩放倍数放大到1.5倍:
M=cv.getRotationMatrix2D(center,0,1.5) #旋转并缩放图像
代码运行后的图像为:

图3 放大1.5倍后的图像
其实对比图1、图2和图3,会发现图3对原始图像进行了裁切,这种放大效果和cv2.resize()函数相比不一样,cv2.resize()函数本身不会裁切。
【2.2】cv2.resize()函数缩放
为了实现对比cv2.resize()函数放大效果的对比,调用该函数来放大图像,给出完整代码如下:
python">import cv2 # 引入CV模块# 读取图片
image = cv2.imread('src.png')# 定义放大因子
scale_factor = 1.5# 放大图片,使用立方插值
scaled_image = cv2.resize(image, None, fx=scale_factor, fy=scale_factor, interpolation=cv2.INTER_CUBIC) # INTER_CUBIC插值# 保存结果
cv2.imwrite('scaled_image-001-INTER_CUBIC m15.png', scaled_image)# 显示结果
cv2.imshow('Scaled Image15 ', scaled_image)
cv2.waitKey(0)
cv2.destroyAllWindows()代码运行后的输出效果为:

图4 图片放大1.5倍但没有任何裁切
由图4可见,图片放大了1.5倍,但没有任何裁切。
【3】第三种方法
在前序学习进程中,我们成功实现了对图像的倾斜拉伸,相关链接为:
python学opencv|读取图像(二十九)使用cv2.getAffineTransform()函数倾斜拉伸图像-CSDN博客
文章中已经说明,倾斜拉伸是通过控制图像的顶点实现的。首次启发,我们把图像的顶点按照固定比例缩小和放大,这样就能实现图像的缩放。为此,展开代码测试。
这里使用的原始图像为:

图5
【3.1】缩小
首先给出完整代码:
python">import cv2 as cv # 引入CV模块
import numpy as np #引入numpy模块# 读取图片
src = cv.imread('srcm.png')#设置点
rows=len(src) #读取图像行数
cols=len(src[0]) #读取图像列数
p1=np.zeros((3,2),np.float32) #32位浮点型全0矩阵
p1[0]=[0,0] #第一点
p1[1]=[cols-1,0] #第二点
p1[2]=[0,rows-1] #第三点
p2=np.zeros((3,2),np.float32) #32位浮点型全0矩阵
p2[0]=[0,0] #新的第一点
p2[1]=[0.8*(cols-1),0] #新的第二点
p2[2]=[0,0.8*(rows-1)] #新的第三点#center=(rows/2,cols/2) #旋转中心
#M=np.float32([[1,0,50],#[0,1,200]]) #M矩阵,x=50,y=200
M=cv.getAffineTransform(p1,p2)
#M=cv.getRotationMatrix2D(center,60,0.8) #旋转并缩放图像
dst=cv.warpAffine(src,M,(cols,rows)) #输出图像
cv.imshow('srcm-qxls', dst) # 在屏幕展示绘制圆形的效果
cv.imwrite('srcm-qxls-8.png', dst) # 保存图像
cv.waitKey() # 图像不会自动关闭
cv.destroyAllWindows() # 释放所有窗口
在这里,对新的点设置了0.8倍的缩小因子:
p1=np.zeros((3,2),np.float32) #32位浮点型全0矩阵 p1[0]=[0,0] #第一点 p1[1]=[cols-1,0] #第二点 p1[2]=[0,rows-1] #第三点 p2=np.zeros((3,2),np.float32) #32位浮点型全0矩阵 p2[0]=[0,0] #新的第一点 p2[1]=[0.8*(cols-1),0] #新的第二点 p2[2]=[0,0.8*(rows-1)] #新的第三点
代码运行后的输出效果为:

图6 缩小0.8倍
由图6可见,图像成功缩小为原来的0.8倍。
【3.2】放大
修改缩放因子,把图像放大1.5倍:
p1=np.zeros((3,2),np.float32) #32位浮点型全0矩阵 p1[0]=[0,0] #第一点 p1[1]=[cols-1,0] #第二点 p1[2]=[0,rows-1] #第三点 p2=np.zeros((3,2),np.float32) #32位浮点型全0矩阵 p2[0]=[0,0] #新的第一点 p2[1]=[1.5*(cols-1),0] #新的第二点 p2[2]=[0,1.5*(rows-1)] #新的第三点
此时,会惊喜地发现一个猫猫头:

图7 放大1.5倍
显然,cv2.getAffineTransform()函数在放大图像的时候,也会对图像进行裁切。
【4】效果对比
结合上面的使用效果,会发现:
使用cv2.getRotationMatrix2D()函数、cv2.resize()函数和cv2.getAffineTransform函数均可以实现图像缩放;
在图像缩小效果上,三个函数差不多,只是cv2.getRotationMatrix2D()函数和cv2.getAffineTransform函数会保留原本画布的大小,会看到一些纯色的背景;
在图像放大效果上,三个函数不一样,cv2.getRotationMatrix2D()函数和cv2.getAffineTransform函数会会裁切图像依然会保留原有画布的大小,图像超出画布大小的部分会被裁切,而cv2.resize()函数不会裁切图像,会等比例放大图像的所有部分。
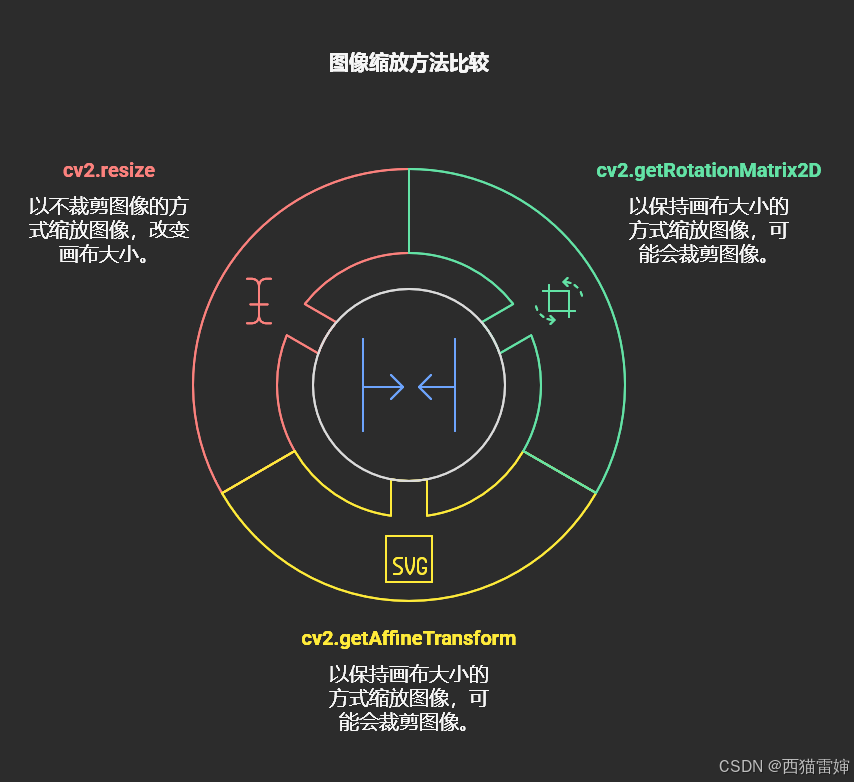
图8 三种图像缩放效果对比