动态规划-----路径问题
- 下降最小路径和
- 1:状态表示
- 2:状态转移方程
- 3 初始化
- 4 填表顺序
- 5 返回值
- 6 代码实现
- 总结:
下降最小路径和

1:状态表示
假设:用dp[i][j]表示:到达[i,j]的最小路径
2:状态转移方程
结合图片分析:

如果图中的A点要到达三角形,那么就会考虑下A点上面的数通过最小路径到达A。
那么通过路径变为 x->A->三角形:
那么我们如何找到到达A点的下降路径呢
由状态表示:用dp[i][j]表示:到达[i,j]的最小路径。
则我们可以转换我到达A点的最小路径为dp[i-1][j-1]或dp[i-1][j]或dp[i-1][j+1]


文字总结:在dp表中每一个位置向下都有3种情况,根据这三种情况可以规划处动态方程:
因为要最小路径和,那么我们就可以在三个路径下取最小的路径,这就要用到min
dp[i][j]= min(dp[i-1][j-1],min(dp[i][j-1],dp[i][j+1]))+d[i][j]----------状态转移方程
3 初始化
初始化的目的是防止越界访问的问题
由状态转移方程得出:dp[i][j]= min(dp[i-1][j-1],min(dp[i][j-1],dp[i][j+1]))+d[i][j]
由状态转移方程可以得出我们需要上方的3个元素分别是:
[i,j-1]、[i,j]、[i,j+1]
所以我们需要添加1行2列:去避免数组越界的问题(圈圆圈的就是会越界的地方)

【注意事项】
1:虚线里面的值是要保证不影响后面的操作第一行就不要影响圆圈的值就可以把第一行初始化成0
对于列:不要影响最小值的比对:min(x,y,z)那么把列初始化为正无穷大
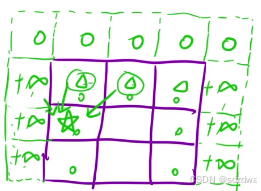
2:d表对应dp表下标的映射
4 填表顺序
填表顺序:从下往上(因为是对于填表左右对状态方程没有什么影响,而上下是有影响的)
5 返回值
返回最后一列的最小值
6 代码实现
class Solution {
public:int minFallingPathSum(vector<vector<int>>& matrix) {//创建dp表int m=matrix.size();int n=matrix[0].size();vector<vector<int>> dp(m+1,vector<int>((n+2),INT_MAX));for(int i=0;i<n+2;i++)//初始化dp[0][i]=0;//填表for(int i=1;i<=m;i++)for(int j=1;j<=n;j++)dp[i][j]=min(dp[i-1][j],min(dp[i-1][j-1],dp[i-1][j+1]))+matrix[i-1][j-1];//返回结果int ret=INT_MAX;for(int i=1;i<=n;i++)ret=min(ret,dp[n][i]);return ret;}
};
总结:
对于路径问题:
第一:分析状态
第二:列出状态方程
第三:初始化(防止越界访问)
第四:填表顺序(由状态方程的出填表顺序)
第五:得出返回值







