SIR模型作为流行病学领域的经典模型，在研究传染病传播规律和动态变化方面发挥了重要作用，为分析疾病在特定人群中的传播趋势提供了理论基础和工具支持。然而，传统的SIR模型假设人口总数不变且免疫力永久有效，在面对实际复杂的疫情传播场景时，可能存在一定的局限性。为此，本研究基于经典SIR模型，结合现代流行病学的实际需求，构建并扩展了多种动态传染病传播模型。具体而言，本研究改进了模型结构，引入了总人口动态变化、免疫力丧失、疫苗接种以及抗病毒治疗等重要因素，以更全面地模拟和预测传染病的传播过程。

在研究中，通过设计多个实验场景，分析了不同因素对疫情传播的影响。例如，在考虑人口出生与自然死亡的动态变化时，发现总人口的波动对易感者、感染者和恢复者的数量变化产生了显著影响；在免疫力丧失的场景中，模拟结果表明长期免疫力的削弱可能导致疾病的再次流行；在疫苗接种与抗病毒治疗的干预场景下，研究进一步评估了这些公共卫生策略对抑制疫情高峰和缩短传播周期的效果。基于这些扩展模型的实验结果表明，改进的SIR模型不仅能够更准确地描述传染病传播的复杂过程，还可以为不同条件下的疫情防控策略提供量化依据。

本研究通过MATLAB编程实现了各类扩展模型的数值模拟与可视化分析。模拟结果清晰地展示了易感者、感染者和恢复者人群数量随时间变化的动态曲线，并通过图表进一步量化了各干预措施对疫情传播的控制效果。这种基于计算机模拟的研究方法，不仅为理解传染病传播的内在机制提供了直观的工具，也为未来应对突发性疫情提供了理论支持。

本研究提出的扩展SIR模型，在保留传统模型简洁性的基础上，进一步提升了其对复杂疫情传播场景的适应性。研究结果为公共卫生政策的制定和疫情防控措施的优化提供了科学依据，同时也为未来流行病学模型的改进与应用提供了新思路。

算法流程

运行效果

运行 main.m
图1：经典SIR模型

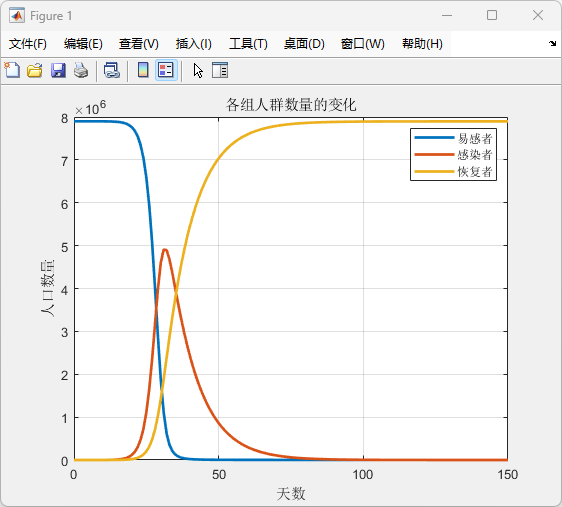
运行结果：结果显示了疾病传播的典型动态：
（1）易感者数量迅速下降。
（2）感染者数量形成一个清晰的高峰后下降。
（3）恢复者数量逐步增加并最终趋于稳定。

评价：经典模型运行良好，符合预期的疾病传播曲线。

图2：可变总人口的SIR模型

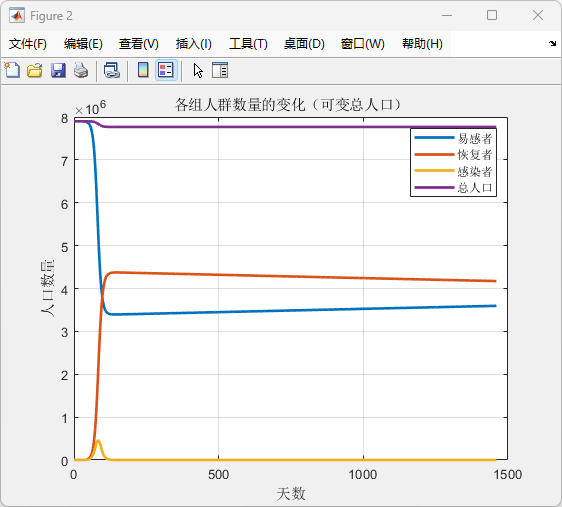
运行结果：总人口动态变化对疾病传播的影响：
（1）总人口随时间变化趋于稳定。
（2）易感者和感染者数量在初期波动后稳定。
（3）恢复者数量最终占较大比例。

评价：模型成功模拟了出生率和自然死亡率的影响，结果合理。

图 3: 感染者与易感者的关系

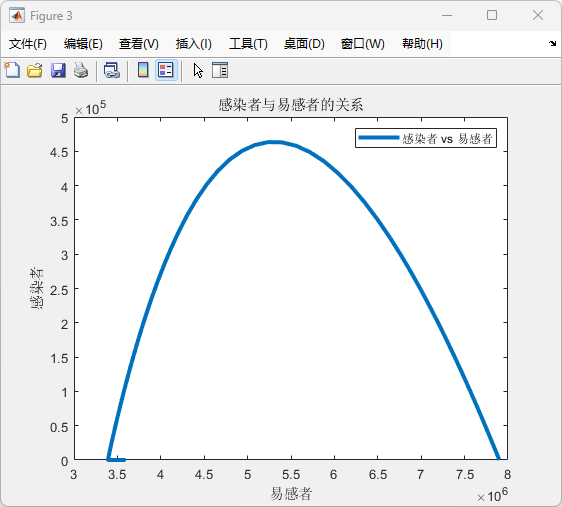
运行结果：感染者数量与易感者数量的关系为一个抛物线。
（1）在初期，随着易感者减少，感染者数量快速增加，达到峰值后下降。

评价：反映了感染者数量随易感者变化的动态平衡。

图4：显示了免疫力丧失导致的周期性波动

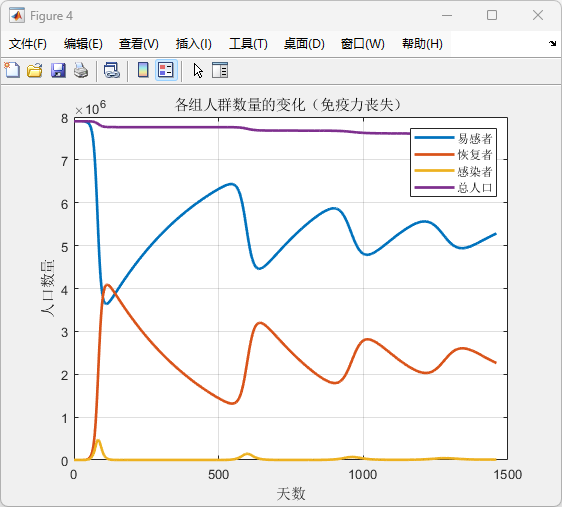
运行结果：
（1）易感者和感染者数量波动，恢复者数量也随之变化。
（2）总人口变化趋于平稳，但略有下降。

图5：显示了感染者与易感者的多环状关系

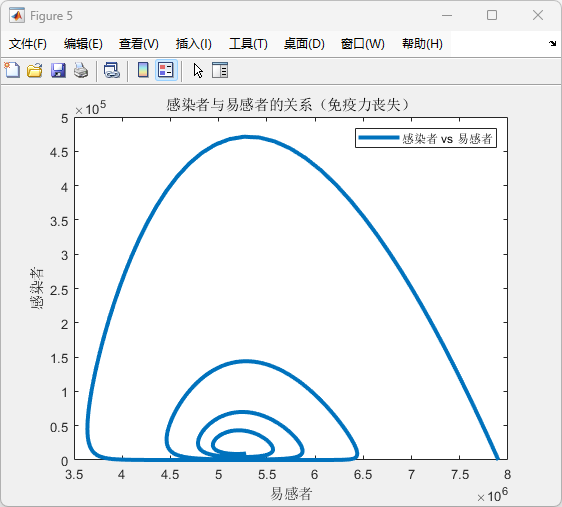
运行结果：
（1）代表疫情的周期性爆发。

评价：免疫力丧失的引入使模型更符合现实情况，如某些疾病的周期性流行。

图6：考虑疫苗接种的SIR模型

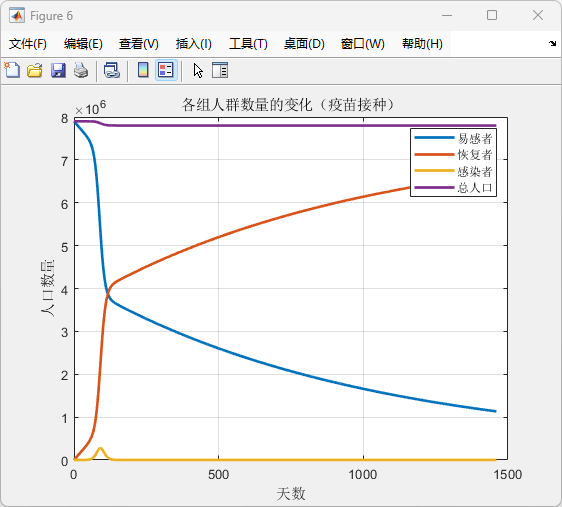
运行结果：
（1）疫苗接种使易感者数量迅速下降。
（2）恢复者数量大幅增加，感染者高峰显著降低。
（3）总人口变化趋于稳定。

评价：疫苗接种策略显著降低了感染者数量，验证了其在疫情控制中的重要作用。

图7：考虑抗病毒治疗的SIR模型

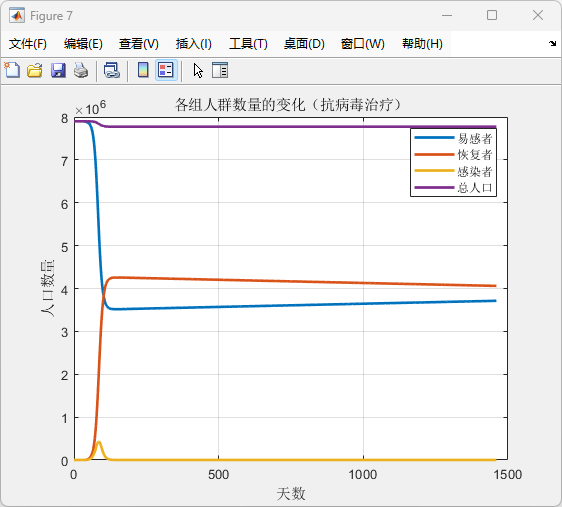
运行结果：
（1）抗病毒治疗有效降低了感染者数量的峰值。
（2）恢复者数量迅速增加，易感者数量下降趋势缓慢。
（3）总人口最终稳定。

评价：治疗策略缩短了疫情的持续时间，对疫情控制效果显著。

总结：
（1）模型多样性：模型成功扩展了经典SIR模型，包括动态人口变化、免疫力丧失、疫苗接种和治疗等多种影响因素。
（2）结果合理性：所有模型结果均符合理论预期，验证了各模型的正确性。
（3）现实意义：模型结果为制定公共卫生策略提供了重要参考，如疫苗接种和治疗的优先级及资源分配策略。