并查集理论基础
并查集主要有两个功能:
- 将两个元素添加到一个集合中。
- 判断两个元素在不在同一个集合
代码模板
int n = 1005; // n根据题目中节点数量而定,一般比节点数量大一点就好
vector<int> father = vector<int> (n, 0); // C++里的一种数组结构// 并查集初始化
void init() {for (int i = 0; i < n; ++i) {father[i] = i;}
}
// 并查集里寻根的过程
int find(int u) {return u == father[u] ? u : father[u] = find(father[u]); // 路径压缩
}// 判断 u 和 v是否找到同一个根
bool isSame(int u, int v) {u = find(u);v = find(v);return u == v;
}// 将v->u 这条边加入并查集
void join(int u, int v) {u = find(u); // 寻找u的根v = find(v); // 寻找v的根if (u == v) return ; // 如果发现根相同,则说明在一个集合,不用两个节点相连直接返回father[v] = u;
}
通过模板,我们可以知道,并查集主要有三个功能。
- 寻找根节点,函数:find(int u),也就是判断这个节点的祖先节点是哪个
- 将两个节点接入到同一个集合,函数:join(int u, int v),将两个节点连在同一个根节点上
- 判断两个节点是否在同一个集合,函数:isSame(int u, int v),就是判断两个节点是不是同一个根节点
模拟过程
(凸显途径合并的过程,每一个join都要画图)
不少录友在接触并查集模板之后,用起来很娴熟,因为模板确实相对固定,但是对并查集内部数据组织方式以及如何判断是否是同一个集合的原理很模糊。
通过以上讲解之后,我再带大家一步一步去画一下,并查集内部数据连接方式。
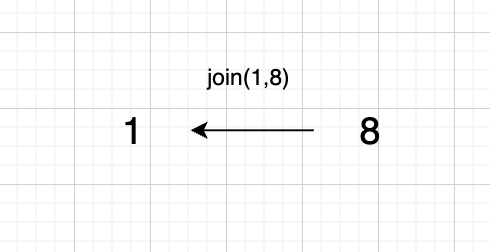
1、
join(1, 8);
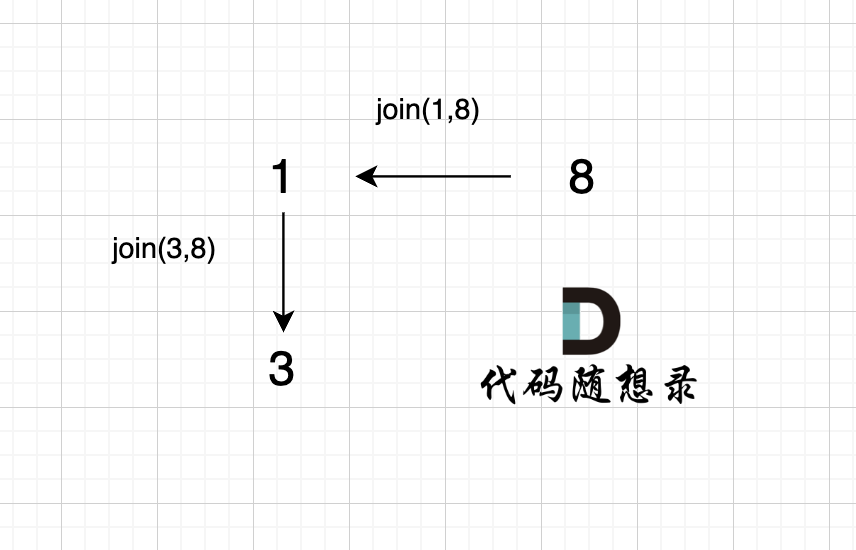
2、
join(3, 8);
有录友可能想,
join(3, 8)在图中为什么 将 元素1 连向元素 3 而不是将 元素 8 连向 元素 3 呢?这一点 我在 「常见误区」标题下已经详细讲解了,因为在
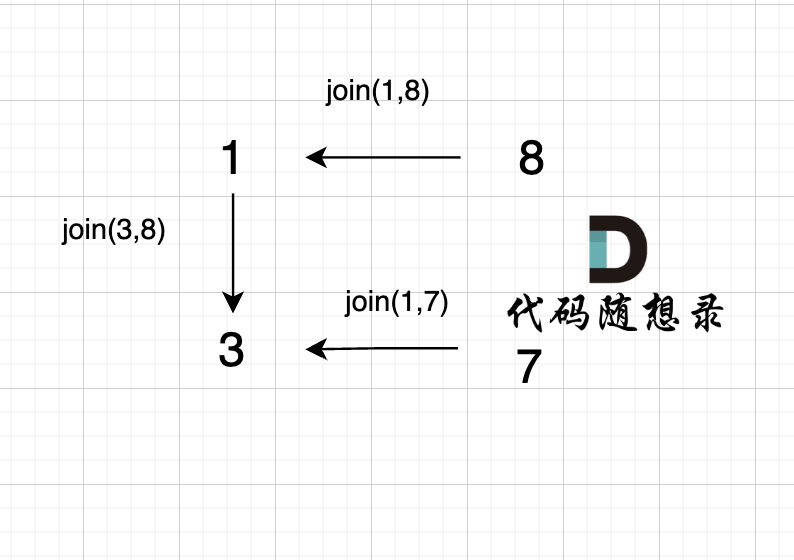
join(int u, int v)函数里 要分别对 u 和 v 寻根之后再进行关联。3、
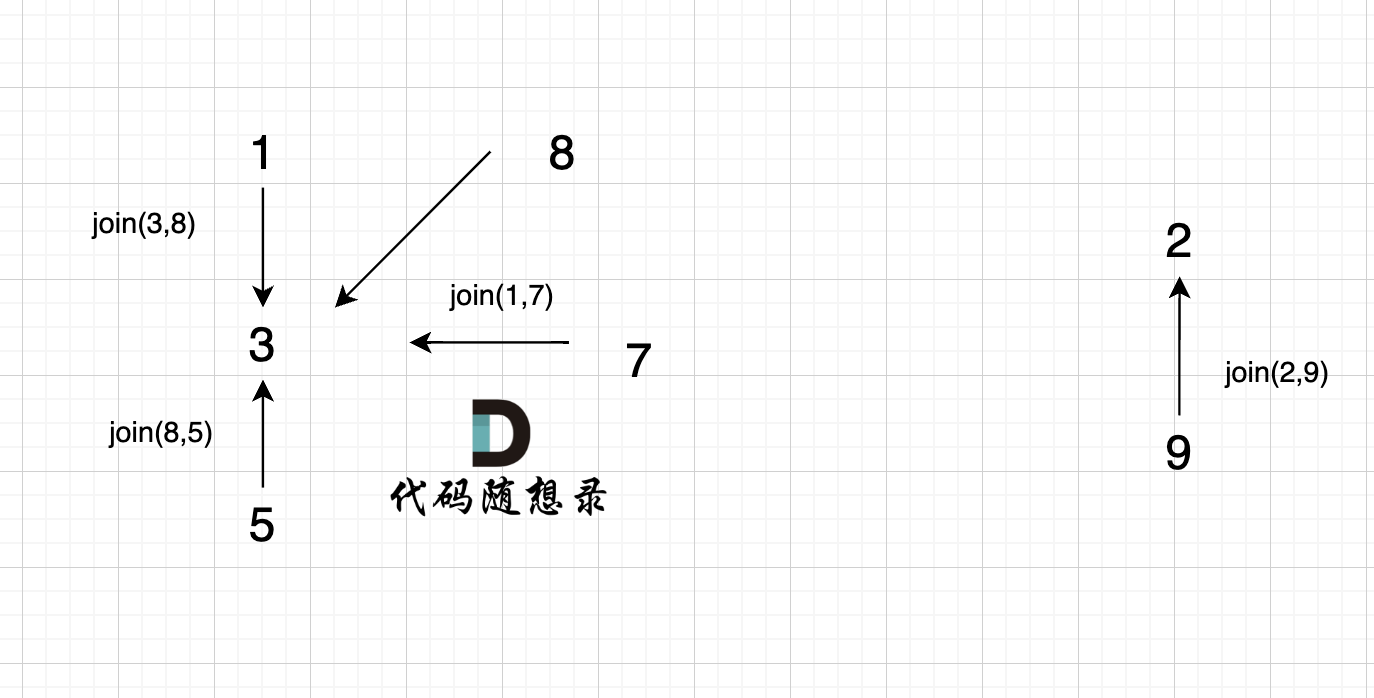
join(1, 7);
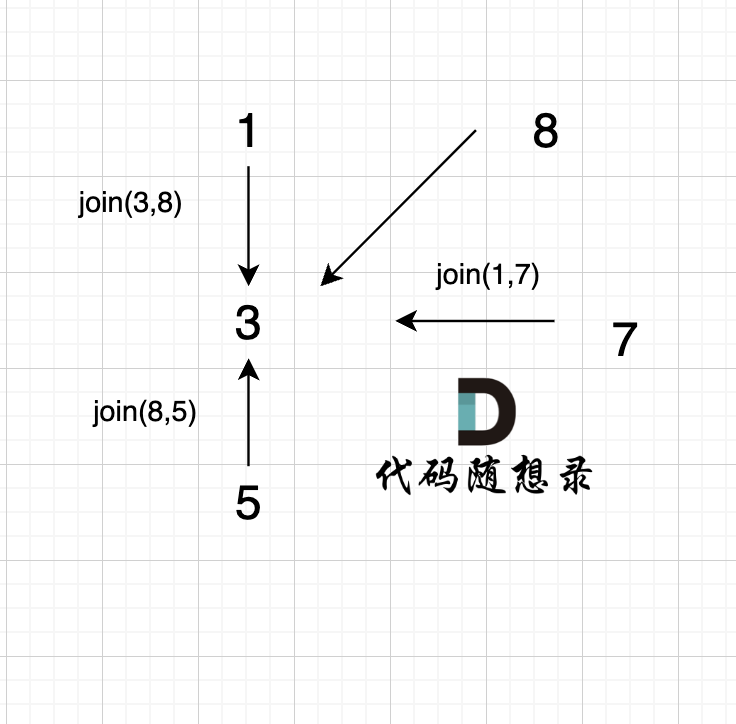
4、
join(8, 5);
这里8的根是3,那么 5 应该指向 8 的根 3,这里的原因,我们在上面「常见误区」已经讲过了。 但 为什么 图中 8 又直接指向了 3 了呢?
因为路经压缩了
即如下代码在寻找根的过程中,会有路径压缩,减少 下次查询的路径长度。
// 并查集里寻根的过程 int find(int u) {return u == father[u] ? u : father[u] = find(father[u]); // 路径压缩 }5、
join(2, 9);
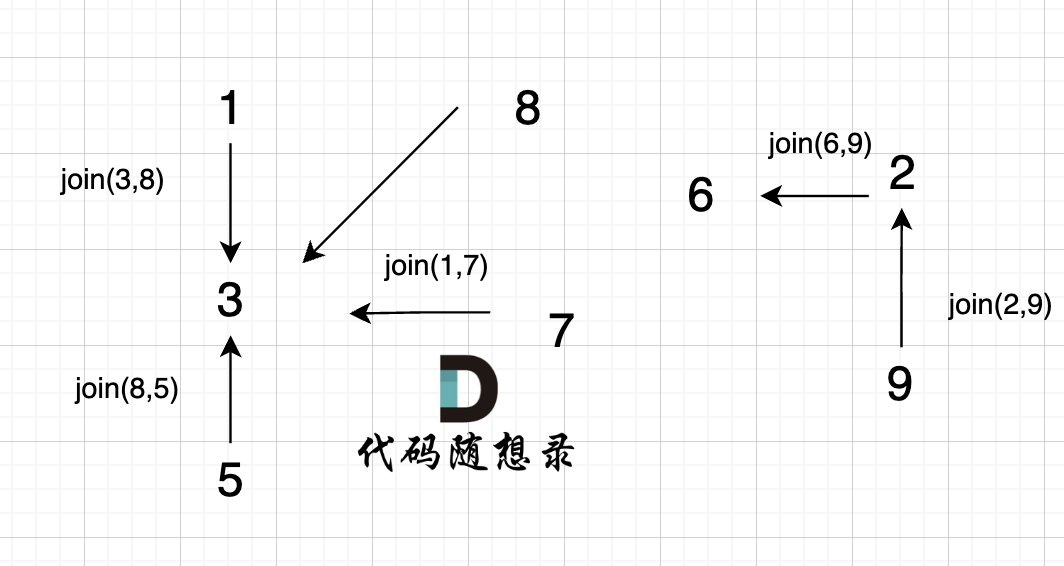
6、
join(6, 9);
这里为什么是 2 指向了 6,因为 9的根为 2,所以用2指向6。
大家看懂这个有向图后,相信应该知道如下函数的返回值了。
cout << isSame(8, 7) << endl; cout << isSame(7, 2) << endl;返回值分别如下,表示,8 和 7 是同一个集合,而 7 和 2 不是同一个集合。
true false
107.寻找存在的路径
107. 寻找存在的路径
题目描述
给定一个包含 n 个节点的无向图中,节点编号从 1 到 n (含 1 和 n )。
你的任务是判断是否有一条从节点 source 出发到节点 destination 的路径存在。
输入描述
第一行包含两个正整数 N 和 M,N 代表节点的个数,M 代表边的个数。
后续 M 行,每行两个正整数 s 和 t,代表从节点 s 与节点 t 之间有一条边。
最后一行包含两个正整数,代表起始节点 source 和目标节点 destination。
输出描述
输出一个整数,代表是否存在从节点 source 到节点 destination 的路径。如果存在,输出 1;否则,输出 0。
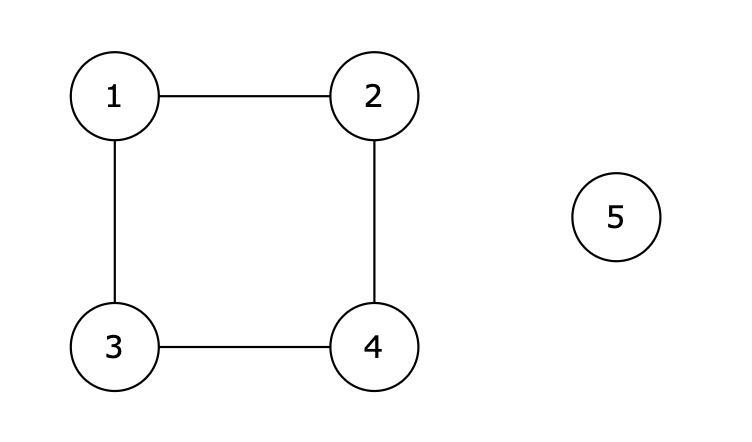
输入示例
5 4 1 2 1 3 2 4 3 4 1 4输出示例
1提示信息
数据范围:
1 <= M, N <= 100。
如何算是同一个集合呢,有边连在一起,就算是一个集合。
此时我们就可以直接套用并查集模板。
使用 join(int u, int v)将每条边加入到并查集。
最后 isSame(int u, int v) 判断是否是同一个根 就可以了。
代码
#include <iostream>
#include <vector>
using namespace std;int n; // 节点数量
vector<int> father = vector<int> (101, 0); // 按照节点大小定义数组大小// 并查集初始化
void init() {for (int i = 1; i <= n; i++) father[i] = i;
}
// 并查集里寻根的过程
int find(int u) {return u == father[u] ? u : father[u] = find(father[u]);
}// 判断 u 和 v是否找到同一个根
bool isSame(int u, int v) {u = find(u);v = find(v);return u == v;
}// 将v->u 这条边加入并查集
void join(int u, int v) {u = find(u); // 寻找u的根v = find(v); // 寻找v的根if (u == v) return ; // 如果发现根相同,则说明在一个集合,不用两个节点相连直接返回father[v] = u;
}int main() {int m, s, t, source, destination;cin >> n >> m;init();while (m--) {cin >> s >> t;join(s, t);}cin >> source >> destination;if (isSame(source, destination)) cout << 1 << endl;else cout << 0 << endl;
}