给你一个 n x n 的二维数组 grid,它包含范围 [0, n2 - 1] 内的不重复元素。
实现 neighborSum 类:
neighborSum(int [][]grid)初始化对象。int adjacentSum(int value)返回在grid中与value相邻的元素之和,相邻指的是与value在上、左、右或下的元素。int diagonalSum(int value)返回在grid中与value对角线相邻的元素之和,对角线相邻指的是与value在左上、右上、左下或右下的元素。

示例 1:
输入:
["neighborSum", "adjacentSum", "adjacentSum", "diagonalSum", "diagonalSum"]
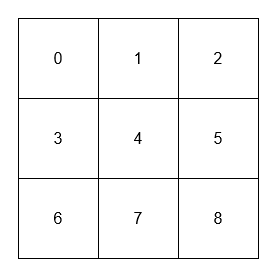
[[[[0, 1, 2], [3, 4, 5], [6, 7, 8]]], [1], [4], [4], [8]]
输出: [null, 6, 16, 16, 4]
解释:
- 1 的相邻元素是 0、2 和 4。
- 4 的相邻元素是 1、3、5 和 7。
- 4 的对角线相邻元素是 0、2、6 和 8。
- 8 的对角线相邻元素是 4。
示例 2:
输入:
["neighborSum", "adjacentSum", "diagonalSum"]
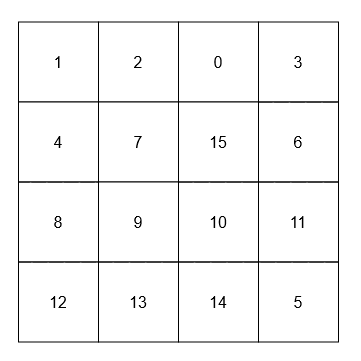
[[[[1, 2, 0, 3], [4, 7, 15, 6], [8, 9, 10, 11], [12, 13, 14, 5]]], [15], [9]]
输出: [null, 23, 45]
解释:
- 15 的相邻元素是 0、10、7 和 6。
- 9 的对角线相邻元素是 4、12、14 和 15。
提示:
3 <= n == grid.length == grid[0].length <= 100 <= grid[i][j] <= n^2 - 1- 所有
grid[i][j]值均不重复。 adjacentSum和diagonalSum中的value均在范围[0, n^2 - 1]内。- 最多会调用
adjacentSum和diagonalSum总共2 * n^2次。
我的解答
java">class NeighborSum {private int[][] grid;private Map<Integer, int[]> pos;private final int[][][] dirs = {{{-1, 0}, {1, 0}, {0, -1}, {0, 1}}, {{-1, -1}, {-1, 1}, {1, -1}, {1, 1}}};public NeighborSum(int[][] grid) {this.grid = grid;this.pos = new HashMap<>();for (int i = 0; i < grid.length; i++) {for (int j = 0; j < grid[0].length; j++) {// 记录数组值和它多对应的索引值pos.put(grid[i][j], new int[]{i, j});}}}public int adjacentSum(int value) {return getSum(value,0);}public int diagonalSum(int value) {return getSum(value,1);}private int getSum(int value, int idx) {int[] p = pos.get(value);int x = p[0], y = p[1];int sum = 0;for (int[] dir : dirs[idx]) {int nx = x + dir[0];int ny = y + dir[1];if (nx >= 0 && nx < grid.length && ny >= 0 && ny < grid[0].length) {sum += grid[nx][ny];}}return sum;}
}/*** Your NeighborSum object will be instantiated and called as such:* NeighborSum obj = new NeighborSum(grid);* int param_1 = obj.adjacentSum(value);* int param_2 = obj.diagonalSum(value);*/

![元素定位和标准流理解[从本质到理解]](https://img-blog.csdnimg.cn/img_convert/37400519458a8a43152a4373320b739f.png)
