个人主页:C++忠实粉丝
欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 C++忠实粉丝 原创多源BFS问题(4)_地图分析
目录
1. 题目链接
2. 题目描述
3. 解法
算法思路 :
代码展示 :
4. 算法总结
1. 题目链接
OJ链接 : 地图分析
2. 题目描述
你现在手里有一份大小为 n x n 的 网格 grid,上面的每个 单元格 都用 0 和 1 标记好了。其中 0 代表海洋,1 代表陆地。
请你找出一个海洋单元格,这个海洋单元格到离它最近的陆地单元格的距离是最大的,并返回该距离。如果网格上只有陆地或者海洋,请返回 -1。
我们这里说的距离是「曼哈顿距离」( Manhattan Distance):(x0, y0) 和 (x1, y1) 这两个单元格之间的距离是 |x0 - x1| + |y0 - y1| 。
示例 1:
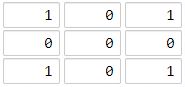
输入:grid = [[1,0,1],[0,0,0],[1,0,1]] 输出:2 解释: 海洋单元格 (1, 1) 和所有陆地单元格之间的距离都达到最大,最大距离为 2。
示例 2:
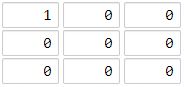
输入:grid = [[1,0,0],[0,0,0],[0,0,0]] 输出:4 解释: 海洋单元格 (2, 2) 和所有陆地单元格之间的距离都达到最大,最大距离为 4。
提示:
n == grid.lengthn == grid[i].length1 <= n <= 100grid[i][j]不是0就是1
3. 解法
算法思路 :
01 矩阵的变型题, 直接用多源bfs解决即可.

代码展示 :
class Solution
{int dx[4] = {0, 0, 1, -1};int dy[4] = {1, -1, 0, 0};
public:int maxDistance(vector<vector<int>>& grid) {int n = grid.size(), m = grid[0].size();vector<vector<int>>dist(n, vector<int>(m, -1));queue<pair<int, int>> q; for(int i = 0; i < n; i++)for(int j = 0; j < m; j++)if(grid[i][j] == 1) {q.push({i, j});dist[i][j] = 0;} int ret = 0;while(q.size()){auto [a, b] = q.front();q.pop();for(int i = 0; i < 4; i++){int x = dx[i] + a, y = dy[i] + b;if(x >= 0 && x < n && y >= 0 && y < m && dist[x][y] == -1){q.push({x, y});dist[x][y] = dist[a][b] + 1;ret = max(ret, dist[x][y]);}}}if(ret) return ret;else return -1;}
};
4. 算法总结
1. 初始化:
dx 和 dy 数组定义了四个方向的移动(右、左、下、上)。
n 和 m 分别代表网格的行数和列数。
创建一个二维 dist 数组,用于记录每个位置到最近的陆地的距离,初始值为 - 1。
使用一个队列 q 来执行广度优先搜索(BFS)。
2. 入队陆地位置:
遍历整个网格,将所有陆地(值为1)的坐标入队,并将其在 dist 中的距离设为0。
3. BFS遍历:
当队列不为空时,取出队首元素(a, b)。
对于每个方向,计算新坐标(x, y)。
如果(x, y) 在网格内且尚未访问(dist[x][y] == -1),将其入队,并更新其距离为 dist[a][b] + 1。
更新最大距离 ret。
4. 返回结果:
最后,如果 ret 大于0,返回最大距离;否则返回 - 1,表示不存在海洋。







