226.翻转二叉树

class Solution:def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:if not root:return tmp =  root.leftroot.left = root.rightroot.right = tmpself.invertTree(root.left)self.invertTree(root.right)return root

101. 对称二叉树

class Solution:def left_right(self, left, right):if (not left and right) or (not right and left):return Falseif not left and not right:return Trueif left.val != right.val:return Falseif self.left_right(left.left, right.right) and self.left_right(left.right, right.left):return Truereturn Falsedef isSymmetric(self, root: Optional[TreeNode]) -> bool:if not root.left and not root.right:return Trueif not root.left or not root.right:return Falsereturn self.left_right(root.left, root.right)

104.二叉树的最大深度

class Solution:def maxDepth(self, root: Optional[TreeNode]) -> int:res_mid = []def bfs(node, level, res_mid):if not node:returnif len(res_mid) == level:res_mid.append([])res_mid[level].append(node.val)bfs(node.left, level + 1, res_mid)bfs(node.right, level + 1, res_mid)bfs(root, 0, res_mid)return len(res_mid)

111.二叉树的最小深度

class Solution:def minDepth(self, root: Optional[TreeNode]) -> int:if not root:return 0if not root.left and not root.right:return 1if not root.left:min_depth = self.minDepth(root.right)+1if not root.right:min_depth = self.minDepth(root.left)+1if root.left and root.right:left = self.minDepth(root.left)+1right = self.minDepth(root.right)+1min_depth = min(left,right)return min_depth

222.完全二叉树的节点个数

class Solution:def countNodes(self, root: Optional[TreeNode]) -> int:res = []def bfs(node,level,res):if not node:returnif len(res) == level:res.append([])res[level].append(node.val)bfs(node.left,level+1,res)bfs(node.right,level+1,res)bfs(root,0,res)final = []for i in res:for j in i:final.append(j)return len(final)

110.平衡二叉树

class Solution:def height(self, node):  # 自下而上if not node:return 1left_height = self.height(node.left)right_height = self.height(node.right)if left_height == -1:return -1if right_height == -1:return -1if abs(left_height - right_height) > 1:return -1else:return 1 + max(left_height, right_height)def isBalanced(self, root: Optional[TreeNode]) -> bool:if self.height(root)!=-1:return Trueelse:return False

257. 二叉树的所有路径

class Solution:def binaryTreePaths(self, root: Optional[TreeNode]) -> List[str]:res = []if not root:return resdef dfs(root,path):path += str(root.val)+'->'if not root.left and not root.right:res.append(path[:-2])returnif root.left:dfs(root.left,path)if root.right:dfs(root.right,path)dfs(root,'')return res

404.左叶子之和

class Solution:def sumOfLeftLeaves(self, root: Optional[TreeNode]) -> int:res = []def dfs(root, path, level):path.append(root.val)if not root.left and not root.right and level == 1: # 判断是否为左子树 , 用level来标记左子树res.append(path[:])return# path.append(root.val)if root.left:dfs(root.left, path, level=1)if root.right:dfs(root.right, path, level=0)dfs(root, [], level=-1)final = 0for i in res:final += int(i[-1])return final

513.找树左下角的值

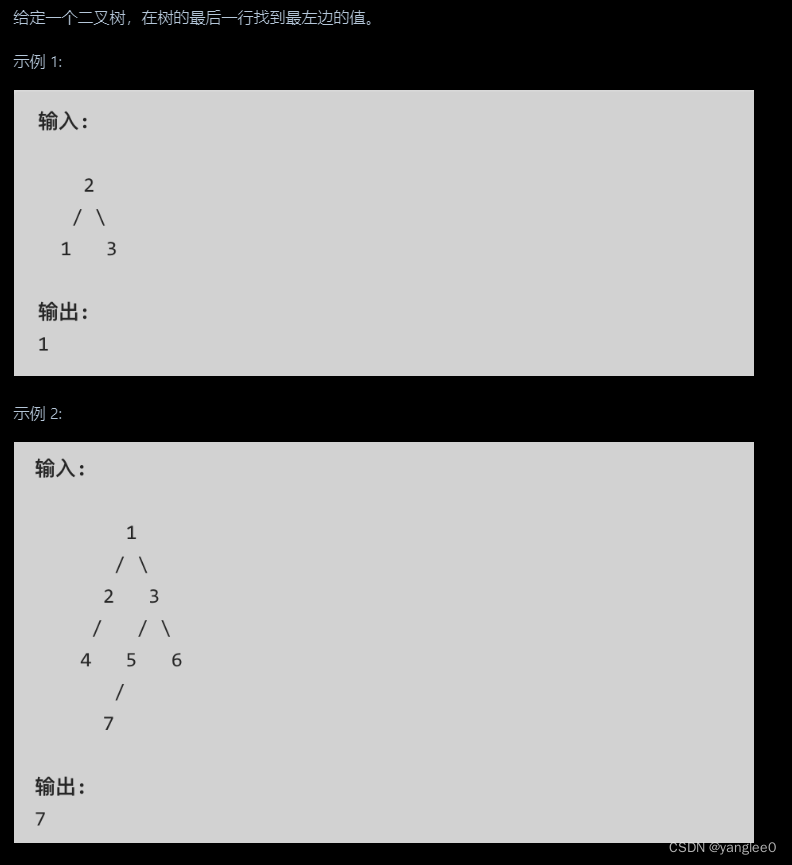
# 层次遍历，反馈最后一层的第一个值就可以了
class Solution:def findBottomLeftValue(self, root: Optional[TreeNode]) -> int:res = []def bfs(node,level):if not node:returnif len(res) == level:res.append([])res[level].append(node.val)bfs(node.left,level+1)bfs(node.right,level+1)bfs(root,0)return res[-1][0]

112. 路径总和

# 路径和问题需要用到回溯了，这里注意回溯的时候要pop一下。和普通递归的地方再进一步。
class Solution:def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:res = []def dfs(node,path):if not node:returnpath.append(node.val)if not node.left and not node.right and sum(path[:]) == targetSum:res.append(path[:])# returndfs(node.left,path)dfs(node.right,path)path.pop()   # 路径问题还是要pop一下dfs(root,[])return True if res else False

113. 路径总和 II

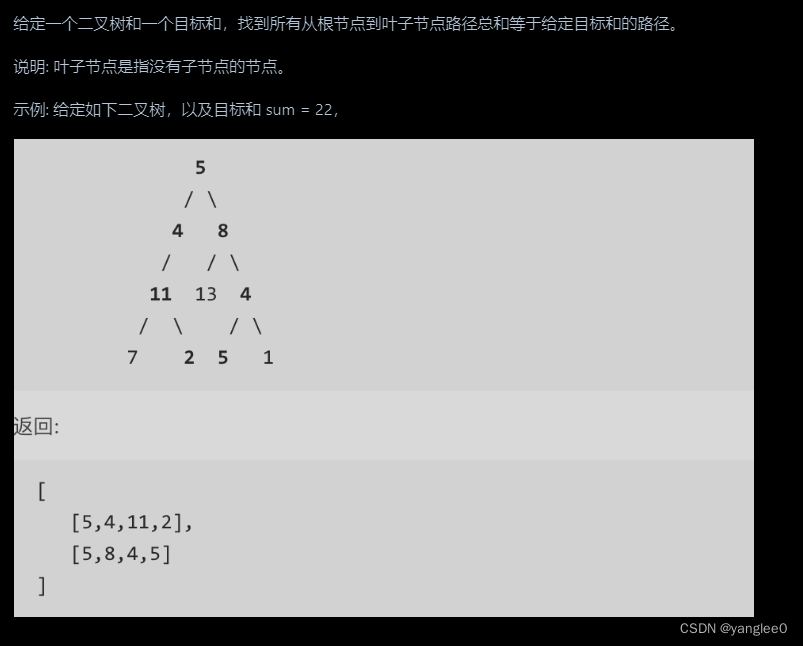
class Solution:def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:res = []def dfs(node,path):if not node:returnpath.append(node.val)if not node.left and not node.right and sum(path[:]) == targetSum:res.append(path[:])returnif node.left:dfs(node.left,path)path.pop()if node.right:dfs(node.right,path)path.pop()   # 路径问题还是要pop一下dfs(root,[])return res

106.从中序与后序遍历序列构造二叉树

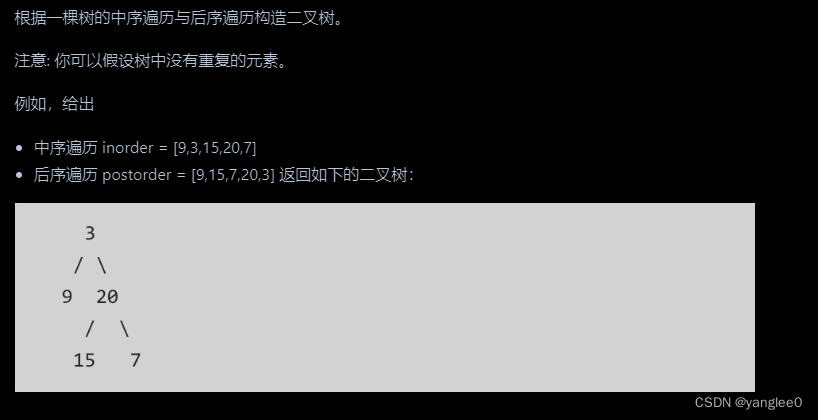
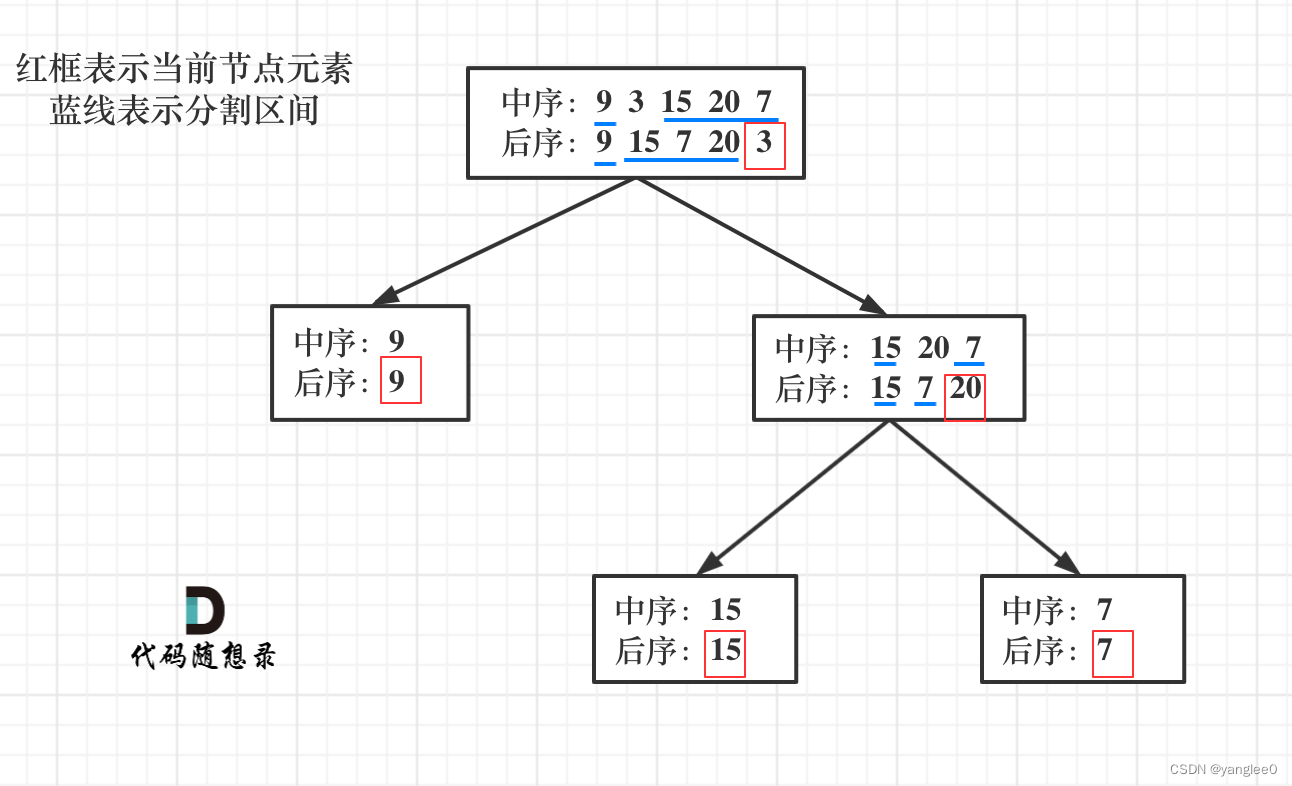第一步：如果数组大小为零的话，说明是空节点了。
第二步：如果不为空，那么取后序数组最后一个元素作为节点元素。
第三步：找到后序数组最后一个元素在中序数组的位置，作为切割点
第四步：切割中序数组，切成中序左数组和中序右数组 （顺序别搞反了，一定是先切中序数组）
第五步：切割后序数组，切成后序左数组和后序右数组
第六步：递归处理左区间和右区间

class Solution:def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:if postorder:root = TreeNode(val = postorder[-1])root_index = inorder.index(postorder[-1])root.left = self.buildTree(inorder[:root_index],postorder[:root_index])root.right = self.buildTree(inorder[root_index+1:],postorder[root_index:-1])return root

105. 从前序与中序遍历序列构造二叉树

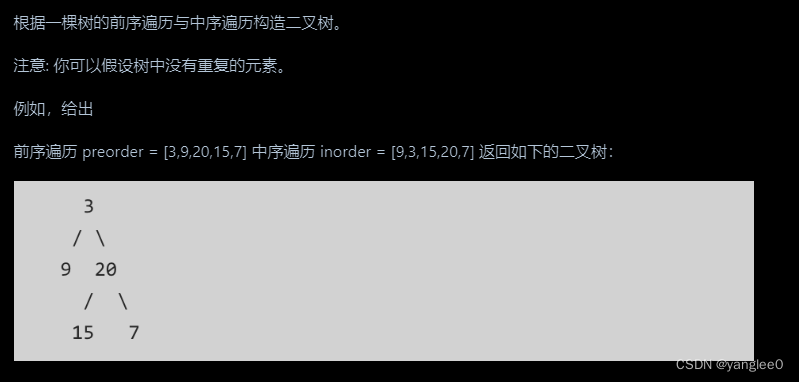
class Solution:def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:if preorder:root = TreeNode(val=preorder[0])root_index = inorder.index(preorder[0])root.left = self.buildTree(preorder[1:root_index+1],inorder[:root_index])root.right = self.buildTree(preorder[root_index+1:],inorder[root_index+1:])return root

654.最大二叉树

class Solution:def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:if nums:root_value = max(nums)root = TreeNode(val = root_value)root_index = nums.index(root_value)root.left = self.constructMaximumBinaryTree(nums[:root_index])root.right = self.constructMaximumBinaryTree(nums[root_index+1:])return root