并查集

正如它的名字一样，并查集（Union-Find）就是用来对集合进行 合并（Union） 与 查询（Find） 操作的一种数据结构。
合并 就是将两个不相交的集合合并成一个集合。
查询 就是查询两个元素是否属于同一集合。

并查集的原理

并查集是一种树型的数据结构，用于处理一些不相交集合的合并及查询问题（即所谓的并、查）。比如说，我们可以用并查集来判断一个森林中有几棵树、某个节点是否属于某棵树等。

组成

并查集主要由一个整型数组pre[ ]和两个函数find( )、join( )构成。

数组 pre[ ] 记录了每个点的前驱节点是谁，函数 find(x) 用于查找指定节点 x 属于哪个集合，函数 join(x,y) 用于合并两个节点 x 和 y 。

现实意义

比如现在有这样的情况：

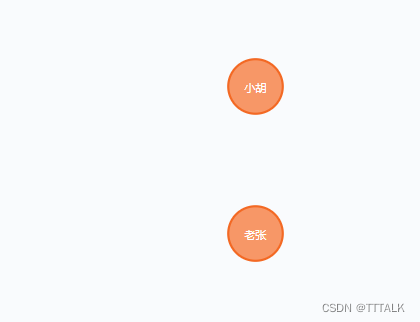
目前饭局有10个人，没两个人之间都可能存在远方亲戚关系，如何将个人分成不同的家庭？现在将个人编号为{0,1,2,3,4,5,6,7,8,9}

-1表示假设每个人之间都不存在亲戚关系

接下来，饭局中的人互相交谈，了解到自己的亲戚关系，因此可以形成不同的家庭。比如：当前是s1：{0,6,7,8},s2：{1,4,9},s3：{2,3,5}形成了不同的家庭。

用树模型表示

因此规定并查集数组有下面的规定：

1. 数组的下标对应集合中元素的编号
2. 数组中如果为负数，负号代表根，数字代表该集合中元素个数
3. 数组中如果为非负数，代表该元素双亲在数组中的下标
4. 如果此时0和1发现也有亲戚关系，那么s1和s2可以合并为一个新的家庭

并查集需要有下面的接口

• 查找元素属于哪个集合
• 查看两个元素是否属于一个集合
• 合并两个集合
• 集合的个数

并查集的实现

创建一个并查集

并查集底层就是一个数组，数组内每个元素初始为-1。

public class unionfindset {public int[] elem;public int usedSize;public unionfindset(int n ){this.elem  = new int[n];Arrays.fill(elem,-1);}public static void main(String[] args) {unionfindset unionfindset = new unionfindset(10);System.out.println(123);}
}

功能实现：

/*** 查找数据 x 的根结点* @param x* @return 下标*/public int findRoot(int x){if (x<0){throw  new IndexOutOfBoundsException("下标不合法，是负数");}while (elem[x]>=0){x = elem[x]; //1 0}return x;}/*** 查询x1 和 x2 是不是同一个集合* @param x1* @param x2* @return*/public boolean isSameUnionFindSet(int x1,int x2){int index1 = findRoot(x1);int index2 = findRoot(x2);if (index1==index2){return true;}else{return false;}}/*** 这是合并操作* @param x1* @param x2*/public void union(int x1,int x2){int index1 = findRoot(x1);int index2 = findRoot(x2);if (index1==index2){return;}else{elem[index1] = elem[index1]+elem[index2];elem[index2]=index1;}}public int getCount(){int count = 1;for (int x:elem){if (x<0){count++;}}return count;}public void print(){for (int x:elem){System.out.print(x+" ");}}

并查集的应用

省份数量

有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。

返回矩阵中 省份 的数量。

来源：力扣（LeetCode）
链接：省份数量

class Solution {public int findCircleNum(int[][] isConnected) {int n = isConnected.length;unionfindset ufs = new unionfindset(n);for(int i = 0;i < isConnected.length;i++) {for(int j = 0;j < isConnected[i].length;j++) {if(isConnected[i][j] == 1) {ufs.union(i,j);}}}return ufs.getCount();}}
class unionfindset {public int[] elem;public int usedSize;public unionfindset(int n ){this.elem  = new int[n];Arrays.fill(elem,-1);}/*** 查找数据 x 的根结点* @param x* @return 下标*/public int findRoot(int x){if (x<0){throw  new IndexOutOfBoundsException("下标不合法，是负数");}while (elem[x]>=0){x = elem[x]; //1 0}return x;}/*** 查询x1 和 x2 是不是同一个集合* @param x1* @param x2* @return*/public boolean isSameUnionFindSet(int x1,int x2){int index1 = findRoot(x1);int index2 = findRoot(x2);if (index1==index2){return true;}else{return false;}}/*** 这是合并操作* @param x1* @param x2*/public void union(int x1,int x2){int index1 = findRoot(x1);int index2 = findRoot(x2);if (index1==index2){return;}else{elem[index1] = elem[index1]+elem[index2];elem[index2]=index1;}}public int getCount(){int count = 0;for (int x:elem){if (x<0){count++;}}return count;}public void print(){for (int x:elem){System.out.print(x+" ");}}
}

等式方程的可满足性

给定一个由表示变量之间关系的字符串方程组成的数组，每个字符串方程 equations[i] 的长度为 4，并采用两种不同的形式之一："a==b" 或 "a!=b"。在这里，a 和 b 是小写字母（不一定不同），表示单字母变量名。

只有当可以将整数分配给变量名，以便满足所有给定的方程时才返回 true，否则返回 false。

来源：力扣（LeetCode）
链接：等式方程的可满足性

class Solution {//等式的满足性public boolean equationsPossible(String[] equations) {unionfindset ufs = new unionfindset(26);for(int i = 0; i < equations.length;i++) {if(equations[i].charAt(1) == '=') {ufs.union(equations[i].charAt(0)-'a',equations[i].charAt(3)-'a');}}for(int i = 0; i < equations.length;i++) {if(equations[i].charAt(1) == '!') {int index1 = ufs.findRoot(equations[i].charAt(0)-'a');int index2 = ufs.findRoot(equations[i].charAt(3)-'a');if(index1 == index2) return false;}}return true;}public static void main(String[] args) {String[] str = {"a==b","b!=a"};//equationsPossible(str);}}
class unionfindset {public int[] elem;public int usedSize;public unionfindset(int n ){this.elem  = new int[n];Arrays.fill(elem,-1);}/*** 查找数据 x 的根结点* @param x* @return 下标*/public int findRoot(int x){if (x<0){throw  new IndexOutOfBoundsException("下标不合法，是负数");}while (elem[x]>=0){x = elem[x]; //1 0}return x;}/*** 查询x1 和 x2 是不是同一个集合* @param x1* @param x2* @return*/public boolean isSameUnionFindSet(int x1,int x2){int index1 = findRoot(x1);int index2 = findRoot(x2);if (index1==index2){return true;}else{return false;}}/*** 这是合并操作* @param x1* @param x2*/public void union(int x1,int x2){int index1 = findRoot(x1);int index2 = findRoot(x2);if (index1==index2){return;}else{elem[index1] = elem[index1]+elem[index2];elem[index2]=index1;}}public int getCount(){int count = 0;for (int x:elem){if (x<0){count++;}}return count;}public void print(){for (int x:elem){System.out.print(x+" ");}}
}