实验八 树
一、实验目的与要求
1)理解树的定义;
2)掌握树的存储方式及基于存储结构的基本操作实现;
二、 实验内容
题目一:采用树的双亲表示法根据输入实现以下树的存储,并实现输入给定结点的双亲结点的查找。
双亲表示法的存储结构描述如下:
#define MaxSize 100 //树中最多结点数
typedef struct{ //树的结点定义
char data; //数据元素
int parent; //双亲位置域
}PTNode;
typedef struct{ //树的类型定义
PTNode nodes[MaxSize]; //双亲表示
int n; //结点数
}PTree;
提示:一组连续空间来存储每个结点,同时在每个结点中增设一个伪指针,指示其双亲结点在数组中的位置。根结点的下标为0,其伪指针域为-1。
示列:
题目二:采用树的孩子表示法,实现以上树的存储,要求实现输入结点查找输出该结点的所有孩子结点,没有孩子结点输出-1。(选做)
存储结构描述
#define MaxSize 100
typedef struct ChildNode{ //链表中每个结点的定义
//链表中每个结点存储的不是数据本身,而是数据在数组中存储的位置下标
int child;
struct ChildNode *next;
}ChildNode;
typedef struct{ //树中每个结点的定义
char data; //结点的数据类型
ChildNode *firstchild; //孩子链表头指针
}CHNode;
typedef struct{
CHNode nodes[MaxSize]; //存储结点的数组
int n;
}CTree;
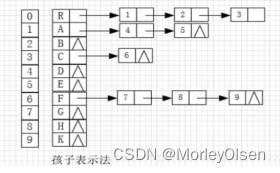
示列:
三、实验结果
1)请将调试通过的运行结果截图粘贴在下面,并说明测试用例和运行过程。
2)请将源代码cpp文件和实验报告一起压缩上传。
第一题:
运行结果:
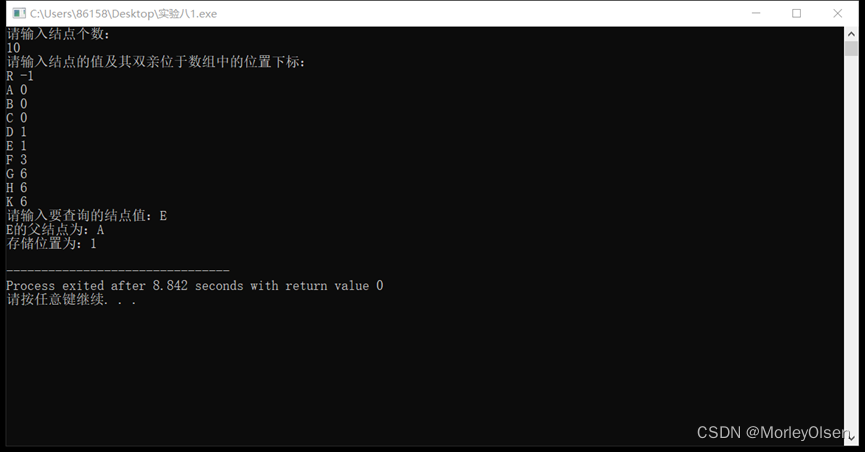
测试用例和运行过程:
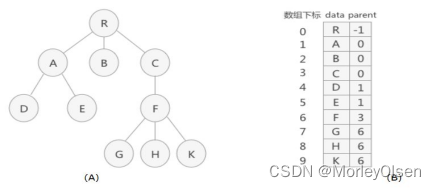
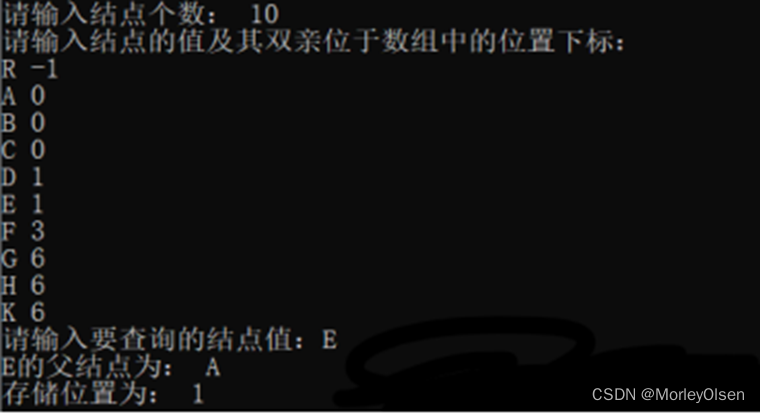
如第一题A图和B图所示,测试用例为该树,各个结点对应的data和parent分别为{ (R,-1) , (A,0) , (B,0) , (C,0) , (D,1) , (E,1) , (F,3) , (G,6) , (H,6) , (K,6) }。
主函数首先创建一个树,通过构造树函数CreateTree依次录入结点的值及其双亲位于数组中的位置下标,再输入需要查询的结点值,通过查找结点函数SearchNode中的for循环遍历各个结点,当且仅当结点值匹配时,输出其父结点和存储位置,然后跳出循环。
最终结果如运行截图所示。
实验代码:
#include <iostream>
#include <cstdio>
using namespace std;#define MaxSize 100 //树中最多结点数
typedef struct{ //树的结点定义char data; //数据元素int parent; //双亲位置域
}PTNode;typedef struct{ //树的类型定义PTNode nodes[MaxSize]; //双亲表示int n; //结点数
}PTree;//构造树
void CreateTree(PTree *T){int i=0;cout<<"请输入结点个数:"<<endl;cin>>T->n ;cout<<"请输入结点的值及其双亲位于数组中的位置下标:"<<endl;for( ;i<T->n ;i++){ cin>>T->nodes[i].data>>T->nodes[i].parent ;}return;
}//查找结点信息
void SearchNode(PTree *T,char e){int i=0,flag=0;for( ;i<T->n ;i++){if(T->nodes[i].data ==e){flag=1;cout<<e<<"的父结点为:"<<T->nodes[T->nodes[i].parent].data<<endl;cout<<"存储位置为:"<<T->nodes[i].parent <<endl;break;}}if(flag==0){cout<<"NOT FOUND"<<endl;}
}int main(){PTree T;CreateTree(&T);cout<<"请输入要查询的结点值:";char element;cin>>element;SearchNode(&T,element);return 0;
}
第二题:
运行结果:
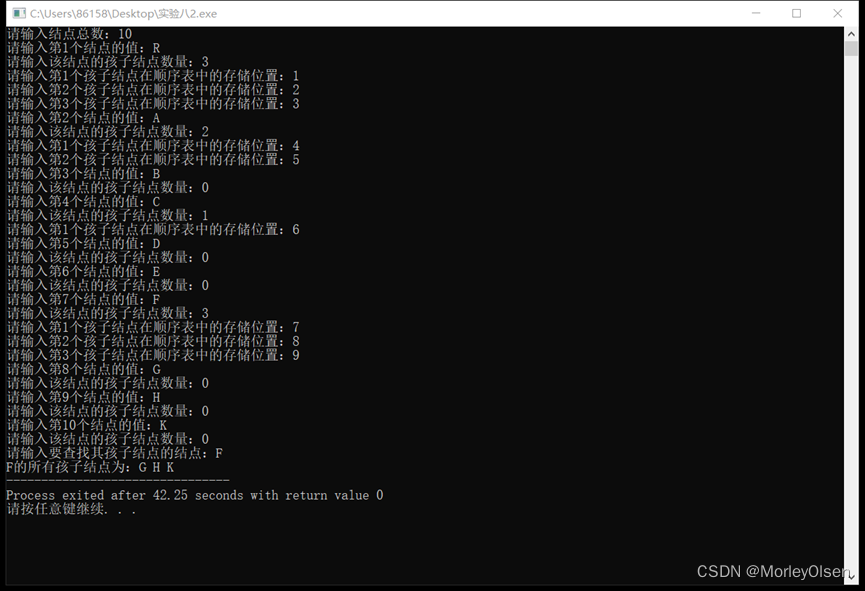
测试用例和运行过程:
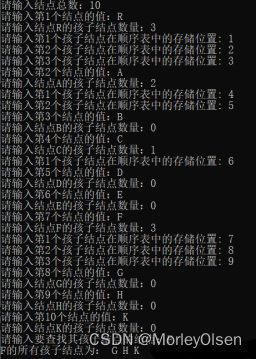
如第二题的图所示,测试用例为该树,只有R,A,C,F结点具有孩子结点,其余均为叶子结点。
主函数首先创建一个树,通过构造树函数CreateTree,首先录入结点的总数,再通过外层for循环依次输入每一个结点的值、当前结点的孩子结点数量,紧接着通过内层for循环依次输入当前结点的孩子结点在顺序表中存储的位置,最终完成树的创建。然后通过查找孩子结点函数SearchChild,输入要查找其孩子结点的结点,通过for循环查找元素一致的结点,确定之后判断孩子是否为空,若非空则通过while循环输出每一个非空的孩子结点。
最终结果如运行截图所示。
实验代码:
#include <iostream>
#include <cstdio>
#include <malloc.h>
using namespace std;#define MaxSize 100
typedef struct ChildNode{ //链表中每个结点的定义//链表中每个结点存储的不是数据本身,而是数据在数组中存储的位置下标int child;struct ChildNode *next;
}ChildNode;typedef struct{ //树中每个结点的定义char data; //结点的数据类型ChildNode *firstchild; //孩子链表头指针
}CHNode;typedef struct{CHNode nodes[MaxSize]; //存储结点的数组int n;
}CTree;//实现输入结点查找输出该结点的所有孩子结点,没有孩子结点输出-1//创建树
void CreateTree(CTree *T){cout<<"请输入结点总数:";cin>>T->n;int i=0;for( ;i<T->n;i++){cout<<"请输入第"<<i+1<<"个结点的值:";cin>>T->nodes[i].data;cout<<"请输入该结点的孩子结点数量:";int num;cin>>num;ChildNode *m=NULL;int j=0;for( ;j<num;j++){ChildNode *s=(ChildNode *)malloc(sizeof(ChildNode)); cout<<"请输入第"<<j+1<<"个孩子结点在顺序表中的存储位置:";cin>>s->child;s->next = NULL;if(j==0){T->nodes[i].firstchild = s;m=s;}else{m->next = s;m=s;}}}
}//查找孩子结点
void SearchChild(CTree *T){char e;cout<<"请输入要查找其孩子结点的结点:";cin>>e;int flag=-1,i=0;for( ;i<T->n ;i++){if(T->nodes[i].data == e){flag=i;break;}} if(flag==-1){cout<<"Not Found"<<endl;return;}ChildNode *p=T->nodes[flag].firstchild;if(p==NULL){cout<<"此结点为叶子结点"<<endl;return;}cout<<e<<"的所有孩子结点为:";while(p!=NULL){cout<<T->nodes[p->child].data<<" ";p=p->next;}
}int main(){CTree T;int i=0;CreateTree(&T);SearchChild(&T);return 0;
}
其他:
#include<iostream>
using namespace std;#define MaxSize 100 //树中最多结点数typedef struct{ //树的结点定义char data; //数据元素int parent; //双亲位置域
}PTNode;typedef struct{ //树的类型定义PTNode nodes[MaxSize]; //双亲表示int n; //结点数
}PTree;void Parent_PT(PTree &ptree,char m){int i;for(i=0;(i<ptree.n)&&(ptree.nodes[i].data!=m);i++);if(i>=ptree.n) cout<<"Node -"<<m<<" is not exist!"<<endl;else{int j=ptree.nodes[i].parent;if(j==-1)cout<<"Node -"<<m<<" has not parent!"<<endl;else{cout<<m<<"的父结点为:"<<ptree.nodes[j].data<<endl;cout<<ptree.nodes[j].data<<"的储存位置为:"<<j<<endl;}}
}int main(){PTree ptree;cout<<"请输入结点个数:";int num;cin>>num;ptree.n=num;cout<<"请输入结点的值以及双亲位于数组中的位置下标:"<<endl;char m;int q; for(int i=0;i<num;i++){cin>>m;cin>>q;ptree.nodes[i].data=m;ptree.nodes[i].parent=q;}while(1){cout<<"请输入要查询的结点值:";cin>>m;if(m=='#'){cout<<"查询结束!";break; } Parent_PT(ptree,m); } return 0;
} #include<iostream>
using namespace std;#define MaxSize 100typedef struct ChildNode{ //链表中每个结点的定义//链表中每个结点存储的不是数据本身,而是数据在数组中存储的位置下标int child;struct ChildNode *next;
}ChildNode;typedef struct{ //树中每个结点的定义char data; //结点的数据类型ChildNode *firstchild; //孩子链表头指针
}CHNode;typedef struct{CHNode nodes[MaxSize]; //存储结点的数组int n;
}CTree;void Init_tree(CTree &ctree){cout<<"请输入结点总数:";int num;cin>>num;ctree.n=num;for(int i=0;i<num;i++){cout<<"请输入第"<<i+1<<"个结点的值:";char m;cin>>m;ctree.nodes[i].data=m;ctree.nodes[i].firstchild=NULL;cout<<"请输入结点"<<m<<"的孩子结点数:";int cnum;cin>>cnum;if(cnum==0) continue;cout<<"请输入第1个孩子结点在顺序表中的存储位置:";int l;cin>>l;ChildNode *p=new ChildNode;p->child=l;p->next=NULL;ctree.nodes[i].firstchild=p;for(int j=1;j<cnum;j++){cout<<"请输入第"<<j+1<<"孩子结点在顺序表中的存储位置:";cin>>l;ChildNode *q=new ChildNode;q->child=l;q->next=NULL;p->next=q;p=q;}}
}void Children(CTree &ctree,char f){int j;for(j=0;(j<ctree.n)&&(ctree.nodes[j].data!=f);j++);if(j>=ctree.n) cout<<"Node -"<<f<<" is not exist!";else{ChildNode *p=ctree.nodes[j].firstchild;if(!p) cout<<"Node -"<<f<<" has not children!";else{cout<<f<<"的所有孩子结点为: ";cout<<ctree.nodes[p->child].data<<" ";while(p->next!=NULL){p=p->next;cout<<ctree.nodes[p->child].data<<" ";}}}
}void Destroy(CTree &ctree){for(int i=0;i<ctree.n;i++){ChildNode *p=ctree.nodes[i].firstchild;ChildNode *q;if(!p) continue;while(p){q=p;p=p->next;q->next=NULL;delete q;}ctree.nodes[i].firstchild=NULL;}
} int main(){CTree ctree;Init_tree(ctree);//初始化 while(1){cout<<"--------------------------------------"<<endl;cout<<"请输入要查找其孩子结点的结点:"; char f;cin>>f;if(f=='#'){cout<<"查询结束!";break; } Children(ctree,f); cout<<endl;}Destroy(ctree);//释放new出的空间 return 0;
}