最长回文子串

⛅前言

大家好，我是知识汲取者，欢迎来到我的LeetCode热题100刷题专栏！

精选 100 道力扣（LeetCode）上最热门的题目，适合初识算法与数据结构的新手和想要在短时间内高效提升的人，熟练掌握这 100 道题，你就已经具备了在代码世界通行的基本能力。在此专栏中，我们将会涵盖各种类型的算法题目，包括但不限于数组、链表、树、字典树、图、排序、搜索、动态规划等等，并会提供详细的解题思路以及Java代码实现。如果你也想刷题，不断提升自己，就请加入我们吧！QQ群号：827302436。我们共同监督打卡，一起学习，一起进步。

博客主页💖：知识汲取者的博客

LeetCode热题100专栏🚀：LeetCode热题100

Gitee地址📁：知识汲取者 (aghp) - Gitee.com

Github地址📁：Chinafrfq · GitHub

题目来源📢：LeetCode 热题 100 - 学习计划 - 力扣（LeetCode）全球极客挚爱的技术成长平台

PS：作者水平有限，如有错误或描述不当的地方，恳请及时告诉作者，作者将不胜感激

🔒题目

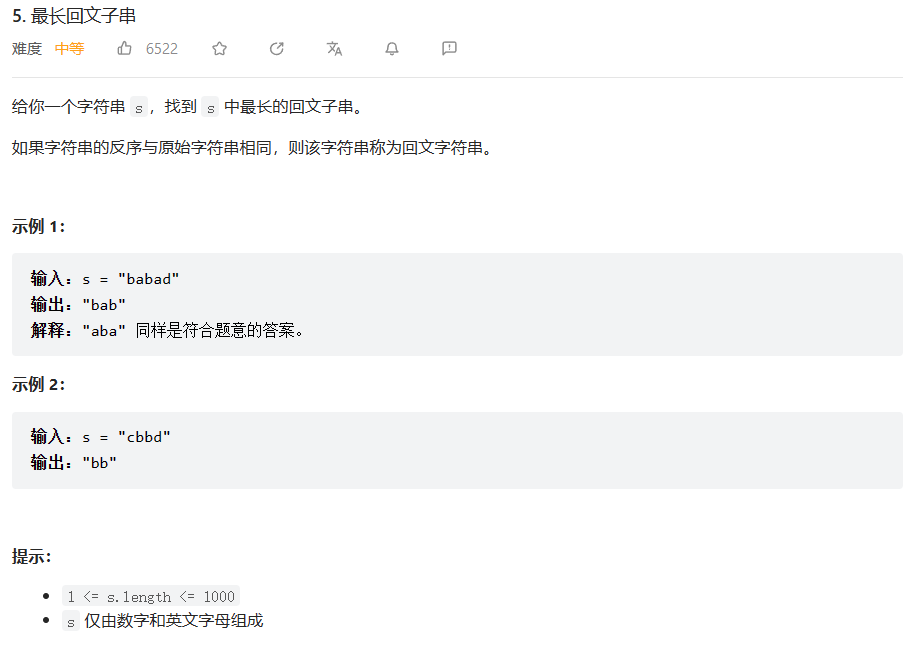
原题链接：5. 最长回文子串 - 力扣（LeetCode）

在这里插入图片描述

🔑题解

解法一：暴力枚举

这个方法简单、粗暴，但是想通过显然是想多了🤣LeetCode还没有这么水

解题思路很简单，这里也就不展开来讲了，主要是对字符串所有可能出现的子串进行一个判断，然后得到最大子串。

我这段代码有一个小注意点，那就是二层遍历要取等，因为substring方法是包前不包后的，如果不取等，当s的长度为2时，比如“aa”，最终的结果仍会是a，而不是aa，因为不取等压根就无法截取到第二个a

/*** @author ghp* @title 最长回文子串*/
class Solution {public String longestPalindrome(String s) {if (s.length() == 1){return s;}int max = Integer.MIN_VALUE; // 记录当前最大回文子串的长度String result = null; // 记录最大回文子串// 遍历所有子串for (int i = 0; i < s.length(); i++) {for (int j = i + 1; j <= s.length(); j++) {String target = s.substring(i, j);// 判断是否是当前最大回文串if (isPalindrome(target) && target.length() > max) {max = target.length();result = target;}}}return result;}/*** 判断是否是回文字符串* @param target* @return true-是 false-否*/private boolean isPalindrome(String target) {StringBuilder sb = new StringBuilder(target);String reverse = sb.reverse().toString();return reverse.equals(target);}
}

复杂度分析：

时间复杂度： $O(n^3)$
空间复杂度： $O (1)$

其中 $n$ 为字符串中字符的个数。之所以是 $n^3$ 是因为reverse()的时间复杂度度是 $O (n)$

在这里插入图片描述

解法二：中心扩散算法（又学到一个新思想 o(￣▽￣)ブ）

主要思想：通过选取中心点，然后以中心点为根据地往两边扩散。

实现步骤：

Step1：选取中心点。由于回文串存在单数与双数，所以中心点选取存在两种方式，如果是奇数中心点直接为单个字符，如果是偶数中心点直接为两个字符之间的间隔
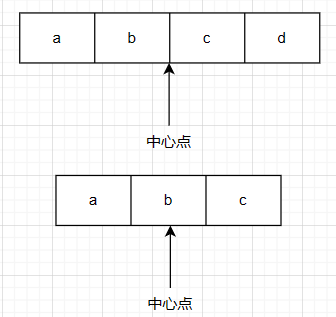
Step2：以中心点为根据地，往两边扩散。
Step3：遍历字符串所有的中心点。

需要注意的点是计算回文串的长度，这里可能一下看不出规律，需要手动推导一下

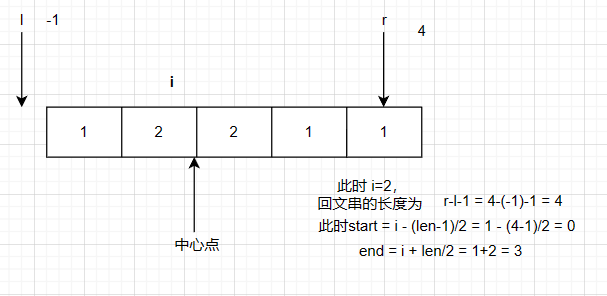
在这里插入图片描述

/*** @author ghp* @title 最长回文子串*/
class Solution {public String longestPalindrome(String s) {if (s.length() == 1) {// 这里可以省略（后面判断兼顾了长度为1的情况），但是还是建议能早返回的尽量找点返回return s;}int start = 0; // 最长回文子串的起始索引int end = 0; // 最长回文子串的结束索引int len = 0;for (int i = 0; i < s.length(); i++) {// 回文子串长度为奇数时int len1 = centerSpread(s, i, i);// 回文子串长度为偶数时int len2 = centerSpread(s, i, i + 1);// 获取当前最大回文子串的长度len = len1 >= len2 ? len1 : len2;// 计算最大回文传的起点和终点（只有当最大回文串的长度发生变化时才需要重新计算）if (len > end - start) {// 这里的计算公式，可以手动推导一下，有规律start = i - (len - 1) / 2;end = i + len / 2;}}return s.substring(start, end + 1);}/*** 中心扩散** @param s* @param l 中心点左边界* @param r 中心点右边界* @return 中心扩散后能够形成的 最长回文子串的长度*/private int centerSpread(String s, int l, int r) {while (l >= 0 && r <= s.length() && s.charAt(l) == s.charAt(r)) {l--;r++;}return r - l - 1;}
}

复杂度分析：

时间复杂度： $O(n^2)$
空间复杂度： $O (1)$

其中 $n$ 为数组中元素的个数

解法三：动态规划

主要思路：我们可以直到回文串的规律，如果一个子串是回文串，那么往他前后在添加一个相同字符，它仍然是回文串。也就是说我们可以得到一个状态方程 $P (i, j) = P (i + 1, j - 1) \land (S i == S j)$ ，因此我们可以从长度较短的回文串往长度较长的回文转进行一个状态转移，从而不断转换，最终得到最长回文子串

public class Solution {public String longestPalindrome(String s) {int len = s.length();if (len < 2) {return s;}int maxLen = 1;int begin = 0;// dp[i][j] 表示 s[i..j] 是否是回文串boolean[][] dp = new boolean[len][len];// 初始化：所有长度为 1 的子串都是回文串for (int i = 0; i < len; i++) {dp[i][i] = true;}char[] charArray = s.toCharArray();// 递推开始// 先枚举子串长度for (int L = 2; L <= len; L++) {// 枚举左边界，左边界的上限设置可以宽松一些for (int i = 0; i < len; i++) {// 由 L 和 i 可以确定右边界，即 j - i + 1 = L 得int j = L + i - 1;// 如果右边界越界，就可以退出当前循环if (j >= len) {break;}if (charArray[i] != charArray[j]) {dp[i][j] = false;} else {if (j - i < 3) {dp[i][j] = true;} else {dp[i][j] = dp[i + 1][j - 1];}}// 只要 dp[i][L] == true 成立，就表示子串 s[i..L] 是回文，此时记录回文长度和起始位置if (dp[i][j] && j - i + 1 > maxLen) {maxLen = j - i + 1;begin = i;}}}return s.substring(begin, begin + maxLen);}
}作者：LeetCode-Solution
链接：https://leetcode.cn/problems/longest-palindromic-substring/solution/zui-chang-hui-wen-zi-chuan-by-leetcode-solution/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。