目录
基本介绍
丢勒-幻方
高阶幻方矩阵
习题
1. 幻方检测
2. durerperm
3. 颜色分配表
4. 幻方矩阵的逆矩阵
5. 幻方矩阵的秩
基本介绍
n×n幻方是含有1到n^2的整数数组,排列后是的每一行、每一列、正反两条主对角线上数字的和都是相同的。对于每个n>2都有很多不同的n×n幻方,函数magic(n)只产生一个特定的幻方。
rot90 将数组旋转 90 度
%% A Few Elementary Array Operations.format shortA = magic(3)sum(A)sum(A')'sum(diag(A))sum(diag(flipud(A)))sum(1:9)/3for k = 0:3rot90(A,k)rot90(A',k)end丢勒-幻方

%% Durer's Melancoliaclear allclose allfigureload durerwhos %数组X中给出像素的值为灰度颜色分配表(olormap) map的索引值image(X)colormap(map)axis image%% Durer's Magic Squarefigureload detailimage(X)colormap(map)axis imageA = magic(4)A = A(:,[1 3 2 4])
高阶幻方矩阵
幻方和
%% Magic Sumn = (3:10)';(n.^3 + n)/2
分三种情况生成幻方矩阵:
(1)n为奇数
(2)n为单偶数(能够被2整除,但是不能被4整除)
(3)n为双偶数(能被4整除)


生成奇数和双偶数幻方矩阵
%% Odd Order 奇数阶幻方矩阵n = 5[I,J] = ndgrid(1:n);A = mod(I+J+(n-3)/2,n);B = mod(I+2*J-2,n);M = n*A + B + 1%% Doubly Even Order n是为双偶数n = 4M = reshape(1:n^2,n,n)';[I,J] = ndgrid(1:n);K = fix(mod(I,4)/2) == fix(mod(J,4)/2);M(K) = n^2+1 - M(K)%% Rank 幻方矩阵的秩figurefor n = 3:20r(n) = rank(magic(n));end bar(r)axis([2 21 0 20])%% Ismagical 判定是否为幻方矩阵help ismagicalfor n = 3:10ismagical(magic(n))end表面图


%% Surf Plots 表面图figurefor n = 9:12subplot(2,2,n-8)surf(rot90(magic(n)))axis tight offtext(0,0,20,num2str(n))endset(gcf,'color','white')

习题
1. 幻方检测
function result = ismagic(A)[m, n] = size(A);% Check if A is a square matrixif m ~= nerror('Input matrix must be a square matrix.');end% Calculate the expected sumexpectedSum = sum(A(1, :));% Check rowsrowSums = sum(A, 2);if ~all(rowSums == expectedSum)result = false;return;end% Check columnscolSums = sum(A, 1);if ~all(colSums == expectedSum)result = false;return;end% Check main diagonalif sum(diag(A)) ~= expectedSumresult = false;return;end% Check secondary diagonal (if matrix size is odd)if mod(n, 2) == 1if sum(diag(flip(A))) ~= expectedSumresult = false;return;endend% If all checks pass, the matrix is a magic squareresult = true;
end
2. durerperm
换行或者换列后,元素和保持不变。
function durerperm(arg)
% DURERPERM Permute Durer's magic square.
% Click on two different rows or columns.
% Is the result still a magic square?if nargin == 0shgload detailimage(X,'buttondownfcn','durerperm(''click'')')colormap(map)axis image offset(gca,'userdata',[])title('Click on two rows or columns')
elseif isequal(arg,'click')cp = get(gca,'currentpoint');a = 35;b = 29;h = 74;w = 75;p = [ceil((cp(1,1)-a)/h) ceil((cp(1,2)-b)/w)];if any(p < 1) || any(p > 4), return, endif isempty(get(gca,'userdata'))set(gca,'userdata',p)elsep1 = get(gca,'userdata');p2 = p;Xp = get(gca,'child');X = get(Xp,'cdata');c = h*(0:3);d = w*(0:3);c([p1(2) p2(2)]) = c([p2(2) p1(2)]);d([p1(1) p2(1)]) = d([p2(1) p1(1)]);i = 0:h-1;j = 0:w-1;I = a+[c(1)+i c(2)+i c(3)+i c(4)+i];J = b+[d(1)+j d(2)+j d(3)+j d(4)+j];K = a+(0:4*h-1);L = b+(0:4*w-1);X(K,L) = X(I,J);set(Xp,'cdata',X)set(gca,'userdata',[])end
end
3. 颜色分配表
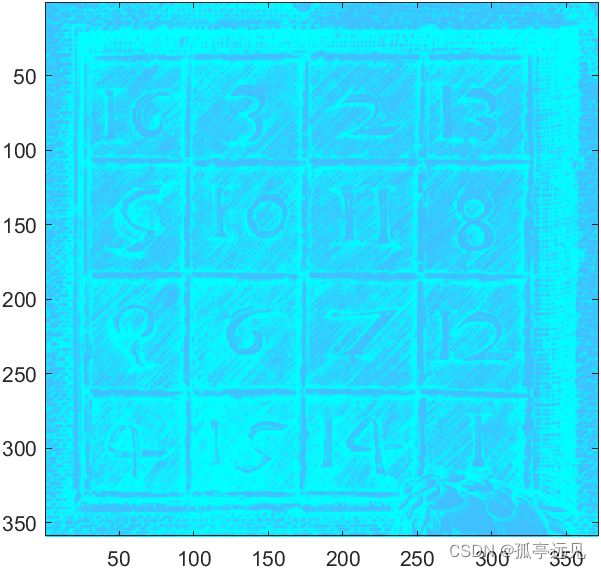
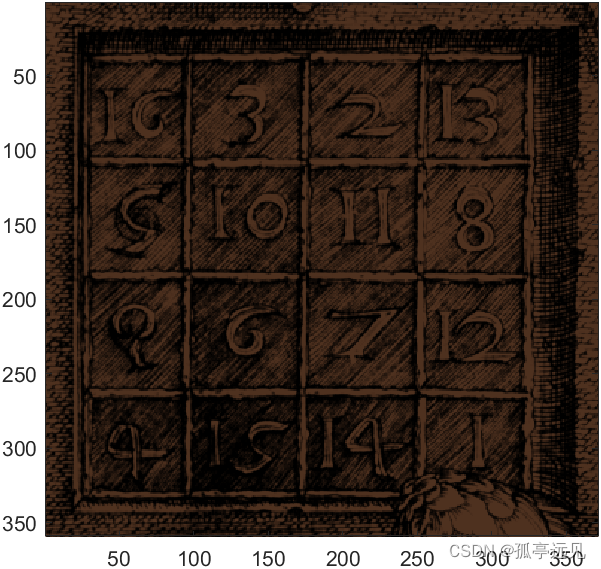
clear load detail; whosmap, captionX(101:130, 101:118)min(min(X))max(max(X))image(X)axis image%colormap(map)colormap("hot")%colormap("cool")%colormap("copper")%colormap("pink")

4. 幻方矩阵的逆矩阵
幻方矩阵的逆矩阵可以通过inv求出
X= inv(magic(n))这个逆矩阵的元素不再保证为正数、整数,但是具有相同的行和列和。
对于偶数阶次n来说,行列数det(magic(n))为0,矩阵为奇异矩阵,逆矩阵不存在。
5. 幻方矩阵的秩
三种不同算法产生的幻方矩阵的秩是不同的:
阶次n 秩
奇数 n
单偶数 n/2+2
双偶数 3