使用 Python 进行深度学习:神经网络(完整教程) 使用TensorFlow构建,绘制和解释人工神经网络
总结
在本文中,我将展示如何使用Python构建神经网络,以及如何使用可视化和创建模型预测解释器向业务解释深度学习。
图片来源:作者 深度学习是一种机器学习,它模仿人类获得某些类型知识的方式,与标准模型相比,它多年来越来越受欢迎。
虽然传统算法是线性的,但深度学习模型(通常是神经网络)堆叠在一个越来越复杂和抽象的层次结构中(因此深度学习中的“深度”)。
神经网络基于一组连接的单元(神经元),就像大脑中的突触一样,可以将信号传递给其他神经元,因此,就像相互连接的脑细胞一样,它们可以以更像人类的方式学习和做出决定。
今天,深度学习是如此流行,以至于许多公司想要使用它,即使他们并不完全理解它。通常,数据科学家首先必须为业务简化这些复杂的算法,然后解释和证明模型的结果,这对于神经网络来说并不总是那么简单。我认为最好的方法是通过可视化。
我将介绍一些有用的 Python 代码,这些代码可以轻松应用于其他类似情况(只需复制、粘贴、运行),并通过注释遍历每一行代码,以便您可以复制示例。
特别是,我将经历:
环境设置,张量流与 pytorch
人工神经网络细分、输入、输出、隐藏层、激活函数
使用深度神经网络进行深度学习
使用张量流/keras进行模型设计
使用python可视化神经网络
模型训练和测试
用形状解释
设置
构建神经网络有两个主要库:TensorFlow(由Google开发)和PyTorch(由Facebook开发)。它们可以执行类似的任务,但前者更适合生产,而后者则适合构建快速原型,因为它更容易学习。
这两个库受到社区和企业的青睐,因为它们可以利用 NVIDIA GPU 的强大功能。这对于处理文本语料库或图像库等大型数据集非常有用,有时甚至是必要的。
在本教程中,我将使用 TensorFlow 和 Keras,这是一个比纯 TensorFlow 和 PyTorch 更用户友好的更高级别的模块,尽管速度有点慢。
第一步是通过终端安装 TensorFlow:
pip install tensorflow 如果要启用GPU支持,可以阅读官方文档或遵循本指南。设置完成后,您的 Python 指令将由您的机器转换为 CUDA 并由 GPU 处理,因此您的模型将运行得非常快。
现在我们可以在笔记本上导入 TensorFlow Keras 的主要模块并开始编码:
from tensorflow.keras import models, layers, utils, backend as K
import matplotlib.pyplot as plt
import shap
人工神经网络
ANN由具有输入和输出维度的层组成。后者由神经元(也称为“节点”)的数量决定,神经元是一个计算单元,通过激活函数连接加权输入(帮助神经元打开/关闭)。
与大多数机器学习算法一样,权重在训练期间随机初始化和优化,以最小化损失函数。
图层可以分组为:
输入层具有将输入向量传递给神经网络的工作。如果我们有一个包含 3 个特征的矩阵(形状 N x 3),则该层将 3 个数字作为输入,并将相同的 3 个数字传递给下一层。
隐藏层代表中间节点,它们对数字进行多次转换以提高最终结果的准确性,输出由神经元的数量定义。
返回神经网络最终输出的输出层。如果我们在做一个简单的二元分类或回归,输出层应该只有 1 个神经元(因此它只返回 1 个数字)。
在具有 5 个不同类的多类分类的情况下,输出层应具有 5 个神经元。
ANN最简单的形式是感知器,一个只有一层的模型,与线性回归模型非常相似。询问感知器内部发生了什么,相当于询问多层神经网络的单个节点内部发生了什么......让我们分解一下。
假设我们有一个包含 N 行、3 个特征和 1 个目标变量(即二进制 1/0)的数据集:

我在 0 到 1 之间放置了一些随机数数据在输入神经网络之前应始终缩放。
就像在所有其他机器学习用例中一样,我们将训练一个模型来逐行使用特征预测目标。让我们从第一行开始:

“训练模型”是什么意思?
在数学公式中搜索最佳参数,以最大程度地减少预测误差。在回归模型,即线性回归中,您必须找到最佳权重,在基于树的模型(即随机森林)中,这是关于找到最佳拆分点......

通常,权重是随机初始化的,然后随着学习的进行进行调整。在这里,我将它们全部设置为 1:

图片来源:作者
到目前为止,我们还没有做任何与线性回归不同的事情。对于业务来说,这很简单。
现在,这里是从线性模型 Σ(xiwi)=Y 到非线性模型 f ( Σ(xiwi)=Y 的升级...输入激活函数。

图片来源:作者
激活函数定义该节点的输出。有很多,甚至可以创建一些自定义函数,您可以在官方文档中找到详细信息并查看此备忘单。如果我们在示例中设置一个简单的线性函数,那么我们与线性回归模型没有区别。
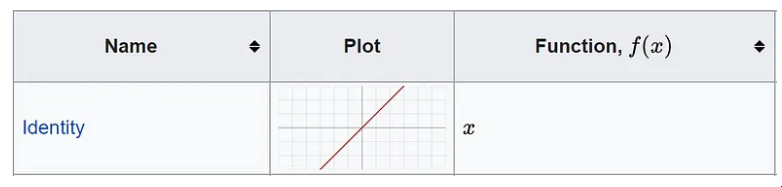
来源:维基百科
我将使用仅返回 1 或 0 的二进制步骤激活函数:

来源:维基百科
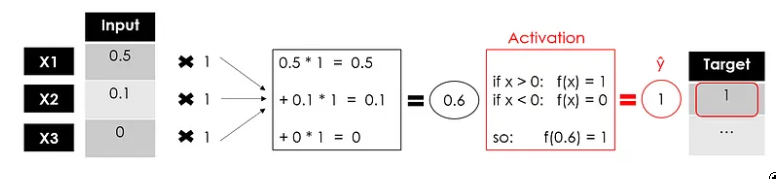
图片来源:作者
我们有感知器的输出,这是一个单层神经网络,它接受一些输入并返回 1 个输出。现在,模型的训练将继续,将输出与目标进行比较,计算误差并优化权重,一次又一次地重复整个过程。
图片来源:作者 这是神经元的常见表示形式:
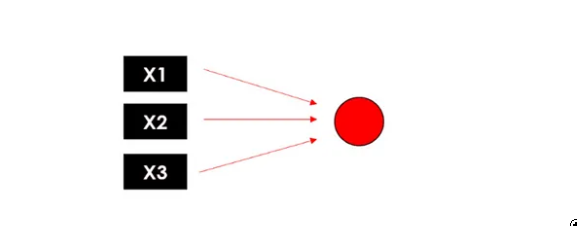
图片来源:作者
深度神经网络
可以说所有的深度学习模型都是神经网络,但并非所有的神经网络都是深度学习模型。一般来说,“深度”学习适用于算法至少有 2 个隐藏层(因此总共 4 层,包括输入和输出)的情况。
想象一下同时复制神经元进程3次:由于每个节点(加权和和激活函数)返回一个值,我们将拥有具有3个输出的第一个隐藏层。
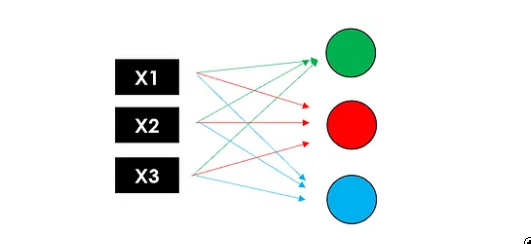
图片来源:作者 现在让我们再次使用这 3 个输出作为第二个隐藏层的输入,该隐藏层返回 3 个新数字。最后,我们将添加一个输出层(仅 1 个节点)以获得模型的最终预测。
图片来源:作者 请记住,这些层可以具有不同数量的神经元和不同的激活函数,并且在每个节点中,权重被训练以优化最终结果。这就是为什么添加的层越多,可训练参数的数量就越多。
现在,您可以查看神经网络的全貌:
图片来源:作者 请注意,为了尽可能简单,我没有提到业务部门可能不感兴趣的某些细节,但数据科学家绝对应该意识到这一点。特别:
偏差:在每个神经元内部,输入和权重的线性组合还包括一个偏差,类似于线性方程中的常数,因此神经元的完整公式为 f( Σ(Xi * Wi ) + 偏置 )
反向传播:在训练期间,模型通过将误差传播回节点并更新参数(权重和偏差)来学习,以最大程度地减少损失。
来源:3Blue1Brown (Youtube) 梯度下降:用于训练神经网络的优化算法,通过在最陡下降的方向上重复步骤来找到损失函数的局部最小值。
source: 3Blue1Brown (Youtube)
Model Design
The easiest way to build a Neural Network with TensorFlow is with the Sequential class of Keras. Let’s use it to make the Perceptron from our previous example, so a model with only one Dense layer. It is the most basic layer as it feeds all its inputs to all the neurons, each neuron providing one output.
model = models.Sequential(name="Perceptron", layers=[
layers.Dense( #a fully connected layer
name="dense",
input_dim=3, #with 3 features as the input
units=1, #and 1 node because we want 1 output
activation='linear' #f(x)=x
)
])
model.summary()

图片来源:作者
摘要函数提供结构和大小的快照(就要训练的参数而言)。在这种情况下,我们只有 4 个(3 个权重和 1 个偏差),所以它非常轻巧。
如果你想使用Keras中尚未包含的激活函数,就像我在可视化示例中展示的二进制步骤函数一样,你必须弄脏原始TensorFlow:
# define the function
import tensorflow as tf
def binary_step_activation(x):
##return 1 if x>0 else 0
return K.switch(x>0, tf.math.divide(x,x), tf.math.multiply(x,0))
# build the model
model = models.Sequential(name="Perceptron", layers=[
layers.Dense(
name="dense",
input_dim=3,
units=1,
activation=binary_step_activation
)
])
现在让我们尝试从感知器转向深度神经网络。可能你会问自己一些问题:
多少层? 正确的答案是“尝试不同的变体,看看什么有效”。
我通常使用 Dropout 处理 2 个密集隐藏层,这是一种通过将输入随机设置为 0 来减少过度拟合的技术。
隐藏层对于克服数据的非线性很有用,因此如果您不需要非线性,则可以避免隐藏层。过多的隐藏层会导致过度拟合。
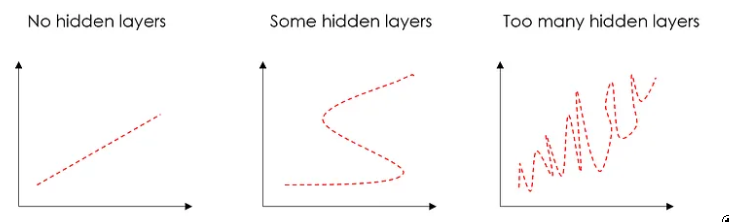
图片来源:作者
有多少神经元? 隐藏神经元的数量应该介于输入层的大小和输出层的大小之间。我的经验法则是(输入数 + 1 输出)/2。
什么是激活功能? 有很多,我们不能说一个绝对更好。无论如何,最常用的是 ReLU,这是一个分段线性函数,只有在为正时才返回输出,并且主要用于隐藏层。
此外,输出层必须具有与预期输出兼容的激活。例如,线性函数适用于回归问题,而 Sigmoid 通常用于分类。
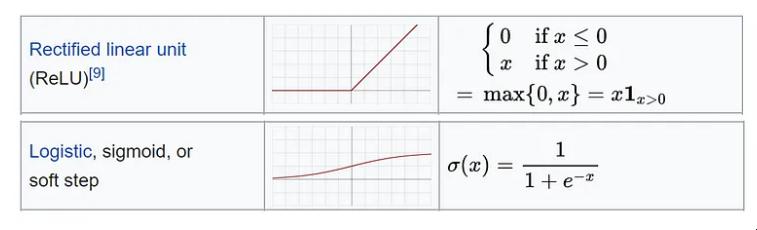
来源:维基百科
我将假设一个包含 N 个特征和 1 个二进制目标变量的输入数据集(很可能是一个分类用例)。
n_features = 10
model = models.Sequential(name="DeepNN", layers=[
### hidden layer 1
layers.Dense(name="h1", input_dim=n_features,
units=int(round((n_features+1)/2)),
activation='relu'),
layers.Dropout(name="drop1", rate=0.2),
### hidden layer 2
layers.Dense(name="h2", units=int(round((n_features+1)/4)),
activation='relu'),
layers.Dropout(name="drop2", rate=0.2),
### layer output
layers.Dense(name="output", units=1, activation='sigmoid')
])
model.summary()

图片来源:作者
请注意,顺序类并不是使用 Keras 构建神经网络的唯一方法。Model 类提供了对层的更大灵活性和控制,可用于构建具有多个输入/输出的更复杂的模型。有两个主要区别:
在顺序类中,需要指定输入层,它隐含在第一个密集层的输入维度中。 这些图层像对象一样保存,可以应用于其他图层的输出,例如:输出 = layer(...)(输入) 这就是如何使用 Model 类来构建我们的感知器和 DeepNN:
# Perceptron
inputs = layers.Input(name="input", shape=(3,))
outputs = layers.Dense(name="output", units=1,
activation='linear')(inputs)
model = models.Model(inputs=inputs, outputs=outputs,
name="Perceptron")
# DeepNN
### layer input
inputs = layers.Input(name="input", shape=(n_features,))
### hidden layer 1
h1 = layers.Dense(name="h1", units=int(round((n_features+1)/2)), activation='relu')(inputs)
h1 = layers.Dropout(name="drop1", rate=0.2)(h1)
### hidden layer 2
h2 = layers.Dense(name="h2", units=int(round((n_features+1)/4)), activation='relu')(h1)
h2 = layers.Dropout(name="drop2", rate=0.2)(h2)
### layer output
outputs = layers.Dense(name="output", units=1, activation='sigmoid')(h2)
model = models.Model(inputs=inputs, outputs=outputs, name="DeepNN")
始终可以检查模型摘要中的参数数量是否与顺序中的参数数量相同。
可视化
请记住,我们正在向企业讲述一个故事,可视化是我们最好的盟友。
我准备了一个函数来绘制人工神经网络的 TensorFlow 模型的结构,这是完整的代码:
'''
Extract info for each layer in a keras model.
'''
def utils_nn_config(model):
lst_layers = []
if "Sequential" in str(model): #-> Sequential doesn't show the input layer
layer = model.layers[0]
lst_layers.append({"name":"input", "in":int(layer.input.shape[-1]), "neurons":0,
"out":int(layer.input.shape[-1]), "activation":None,
"params":0, "bias":0})
for layer in model.layers:
try:
dic_layer = {"name":layer.name, "in":int(layer.input.shape[-1]), "neurons":layer.units,
"out":int(layer.output.shape[-1]), "activation":layer.get_config()["activation"],
"params":layer.get_weights()[0], "bias":layer.get_weights()[1]}
except:
dic_layer = {"name":layer.name, "in":int(layer.input.shape[-1]), "neurons":0,
"out":int(layer.output.shape[-1]), "activation":None,
"params":0, "bias":0}
lst_layers.append(dic_layer)
return lst_layers
'''
Plot the structure of a keras neural network.
'''
def visualize_nn(model, description=False, figsize=(10,8)):
## get layers info
lst_layers = utils_nn_config(model)
layer_sizes = [layer["out"] for layer in lst_layers]
## fig setup
fig = plt.figure(figsize=figsize)
ax = fig.gca()
ax.set(title=model.name)
ax.axis('off')
left, right, bottom, top = 0.1, 0.9, 0.1, 0.9
x_space = (right-left) / float(len(layer_sizes)-1)
y_space = (top-bottom) / float(max(layer_sizes))
p = 0.025
## nodes
for i,n in enumerate(layer_sizes):
top_on_layer = y_space*(n-1)/2.0 + (top+bottom)/2.0
layer = lst_layers[i]
color = "green" if i in [0, len(layer_sizes)-1] else "blue"
color = "red" if (layer['neurons'] == 0) and (i > 0) else color
### add description
if (description is True):
d = i if i == 0 else i-0.5
if layer['activation'] is None:
plt.text(x=left+d*x_space, y=top, fontsize=10, color=color, s=layer["name"].upper())
else:
plt.text(x=left+d*x_space, y=top, fontsize=10, color=color, s=layer["name"].upper())
plt.text(x=left+d*x_space, y=top-p, fontsize=10, color=color, s=layer['activation']+" (")
plt.text(x=left+d*x_space, y=top-2*p, fontsize=10, color=color, s="Σ"+str(layer['in'])+"[X*w]+b")
out = " Y" if i == len(layer_sizes)-1 else " out"
plt.text(x=left+d*x_space, y=top-3*p, fontsize=10, color=color, s=") = "+str(layer['neurons'])+out)
### circles
for m in range(n):
color = "limegreen" if color == "green" else color
circle = plt.Circle(xy=(left+i*x_space, top_on_layer-m*y_space-4*p), radius=y_space/4.0, color=color, ec='k', zorder=4)
ax.add_artist(circle)
### add text
if i == 0:
plt.text(x=left-4*p, y=top_on_layer-m*y_space-4*p, fontsize=10, s=r'$X_{'+str(m+1)+'}$')
elif i == len(layer_sizes)-1:
plt.text(x=right+4*p, y=top_on_layer-m*y_space-4*p, fontsize=10, s=r'$y_{'+str(m+1)+'}$')
else:
plt.text(x=left+i*x_space+p, y=top_on_layer-m*y_space+(y_space/8.+0.01*y_space)-4*p, fontsize=10, s=r'$H_{'+str(m+1)+'}$')
## links
for i, (n_a, n_b) in enumerate(zip(layer_sizes[:-1], layer_sizes[1:])):
layer = lst_layers[i+1]
color = "green" if i == len(layer_sizes)-2 else "blue"
color = "red" if layer['neurons'] == 0 else color
layer_top_a = y_space*(n_a-1)/2. + (top+bottom)/2. -4*p
layer_top_b = y_space*(n_b-1)/2. + (top+bottom)/2. -4*p
for m in range(n_a):
for o in range(n_b):
line = plt.Line2D([i*x_space+left, (i+1)*x_space+left],
[layer_top_a-m*y_space, layer_top_b-o*y_space],
c=color, alpha=0.5)
if layer['activation'] is None:
if o == m:
ax.add_artist(line)
else:
ax.add_artist(line)
plt.show()
让我们在我们的 2 个模型上尝试一下,首先是感知器:
visualize_nn(model, description=True, figsize=(10,8))
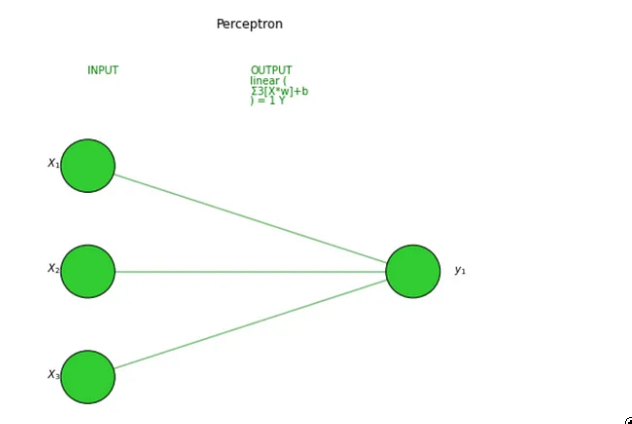
图片来源:作者
然后是深度神经网络:
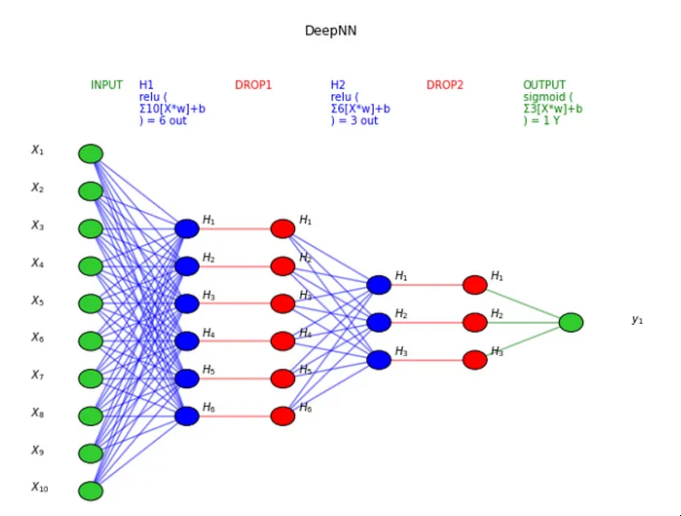
图片来源:作者
TensorFlow也提供了一个绘制模型结构的工具,你可能希望将其用于具有更复杂层(CNN,RNN等)的更复杂的神经网络。有时设置起来有点棘手,如果您有问题,这篇文章可能会有所帮助。
utils.plot_model(model, to_file='model.png', show_shapes=True, show_layer_names=True)
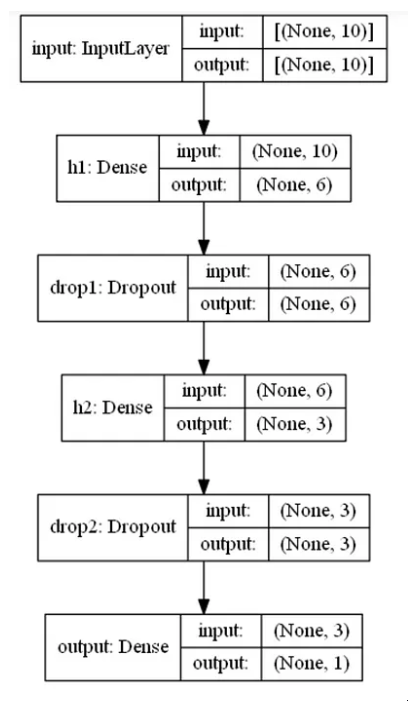
图片来源:作者
这会将此图像保存在笔记本电脑上,因此,如果您只想将其绘制在笔记本上,只需运行以下命令即可删除该文件:
import os
os.remove('model.png')
训练与测试
最后,是时候训练我们的深度学习模型了。为了使它运行,我们必须“编译”,或者换句话说,我们需要定义优化器、损失函数和指标。
我通常使用 Adam 优化器,这是一种梯度下降的替代优化算法(自适应优化器中最好的)。其他参数取决于用例。
在(二元)分类问题中,您应该使用(二元)交叉熵损失,它将每个预测概率与实际类输出进行比较。
至于指标,我喜欢监控准确性和 F1 分数,这是一个结合了精度和召回率的指标(后者必须实现,因为它尚未包含在 TensorFlow 中)。
# define metrics
def Recall(y_true, y_pred):
true_positives = K.sum(K.round(K.clip(y_true * y_pred, 0, 1)))
possible_positives = K.sum(K.round(K.clip(y_true, 0, 1)))
recall = true_positives / (possible_positives + K.epsilon())
return recall
def Precision(y_true, y_pred):
true_positives = K.sum(K.round(K.clip(y_true * y_pred, 0, 1)))
predicted_positives = K.sum(K.round(K.clip(y_pred, 0, 1)))
precision = true_positives / (predicted_positives + K.epsilon())
return precision
def F1(y_true, y_pred):
precision = Precision(y_true, y_pred)
recall = Recall(y_true, y_pred)
return 2*((precision*recall)/(precision+recall+K.epsilon()))
# compile the neural network
model.compile(optimizer='adam', loss='binary_crossentropy',
metrics=['accuracy',F1])
另一方面,在回归问题中,我通常将 MAE 设置为损失,将 R 平方设置为度量。
# define metrics
def R2(y, y_hat):
ss_res = K.sum(K.square(y - y_hat))
ss_tot = K.sum(K.square(y - K.mean(y)))
return ( 1 - ss_res/(ss_tot + K.epsilon()) )
# compile the neural network
model.compile(optimizer='adam', loss='mean_absolute_error',
metrics=[R2])
在开始训练之前,我们还需要确定 Epochs 和 Batches:由于数据集可能太大而无法一次全部处理,因此将其拆分为多个批次(批处理大小越大,需要的内存空间就越多)。
反向传播和随后的参数更新每批发生一次,是整个训练集的一次传递。因此,如果您有 100 个观测值,并且批大小为 20,则需要 5 个批次才能完成 1 个 epoch。批大小应为 2 的倍数(常见:32、64、128、256),因为计算机通常以 2 的幂组织内存。
我倾向于从 100 个 epoch 开始,批大小为 32。
在训练期间,我们希望看到指标得到改善,损失逐个时期减少。此外,最好保留一部分数据 (20%-30%) 进行验证。
换句话说,模型将分离这部分数据,以评估训练之外的每个纪元结束时的损失和指标。
假设你已经把你的数据准备好到一些 X 和 y 数组中(如果没有,你可以简单地生成随机数据,如
import numpy as np
X = np.random.rand(1000,10)
y = np.random.choice([1,0], size=1000)
),您可以按如下方式启动和可视化训练:
# train/validation
training = model.fit(x=X, y=y, batch_size=32, epochs=100, shuffle=True, verbose=0, validation_split=0.3)
# plot
metrics = [k for k in training.history.keys() if ("loss" not in k) and ("val" not in k)]
fig, ax = plt.subplots(nrows=1, ncols=2, sharey=True, figsize=(15,3))
## training
ax[0].set(title="Training")
ax11 = ax[0].twinx()
ax[0].plot(training.history['loss'], color='black') ax[0].set_xlabel('Epochs')
ax[0].set_ylabel('Loss', color='black')
for metric in metrics:
ax11.plot(training.history[metric], label=metric) ax11.set_ylabel("Score", color='steelblue')
ax11.legend()
## validation
ax[1].set(title="Validation")
ax22 = ax[1].twinx()
ax[1].plot(training.history['val_loss'], color='black') ax[1].set_xlabel('Epochs')
ax[1].set_ylabel('Loss', color='black')
for metric in metrics:
ax22.plot(training.history['val_'+metric], label=metric) ax22.set_ylabel("Score", color="steelblue")
plt.show()
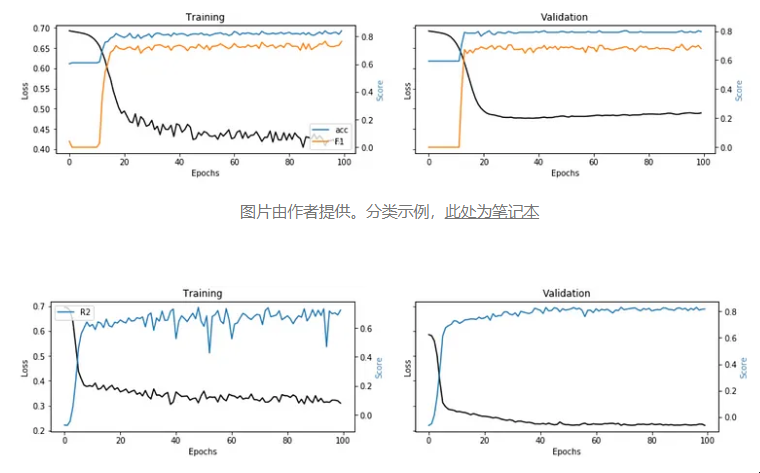
图片由作者提供分类示例
图片由作者提供。回归示例,此处为笔记本 这些图取自两个实际用例,这两个用例将标准机器学习算法与神经网络进行比较(每个图像下的链接)。
可解释性
我们训练并测试了我们的模型,但我们仍然没有说服业务部门相信结果......我们能做什么?很简单,我们构建了一个解释器来证明我们的深度学习模型不是一个黑匣子。
我发现Shap与神经网络配合得很好:对于每个预测,它能够估计每个特征对模型预测值的贡献。基本上,它回答了“为什么模型说这是 1 而不是 0?”的问题。
您可以使用以下代码:
请注意,您也可以在其他机器学习模型(即线性回归、随机森林)上使用此功能,而不仅仅是神经网络。
正如您可以从代码中读到的那样,如果X_train参数保留为 None,我的函数假定它不是深度学习。
让我们在分类和回归示例中对其进行测试:
i = 1
explainer_shap(model,
X_names=list_feature_names,
X_instance=X[i],
X_train=X,
task="classification", #task="regression"
top=10)
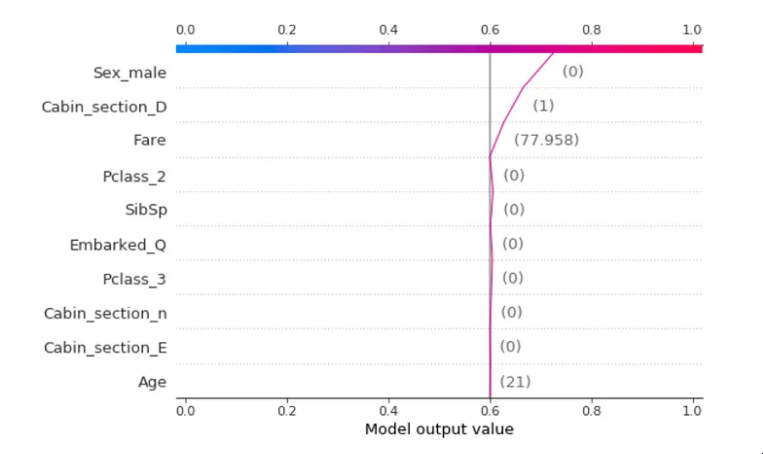
图片由作者提供。分类示例,泰坦尼克号数据集中,预测是“幸存”主要是因为虚拟变量_male=0,所以乘客是女性。
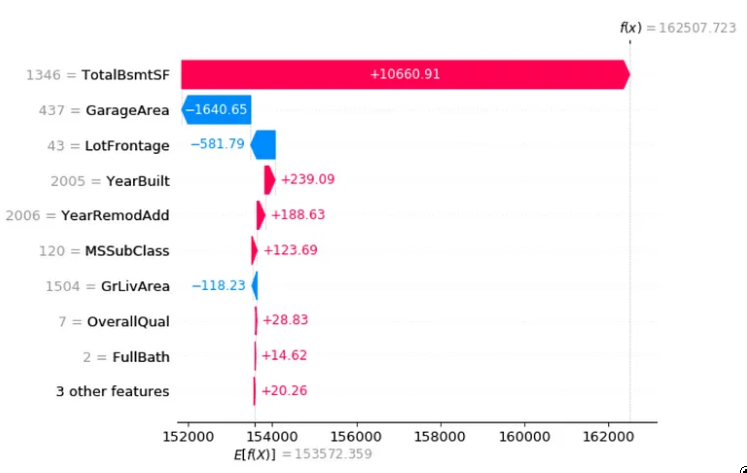
图片由作者提供。回归示例房价数据集,这个房价的主要驱动力是一个大地下室。
结论
本文是一个教程,演示如何设计和构建人工神经网络,无论是深度的还是非深度的。 我一步一步地分解了单个神经元内部发生的事情,更普遍地说是层内发生的事情。我让这个故事变得简单,就好像我们正在向业务部门解释深度学习一样,使用了大量的可视化。
在本教程的第二部分中,我们使用TensorFlow创建了一些神经网络,从感知器到更复杂的神经网络。然后,我们训练了深度学习模型,并评估了它在分类和回归用例中的可解释性。
本文由 mdnice 多平台发布