文章目录
- 64. 最小路径和:
- 样例 1:
- 样例 2:
- 提示:
- 分析:
- 题解:
- rust:
- go:
- c++:
- python:
- java:
64. 最小路径和:
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
样例 1:
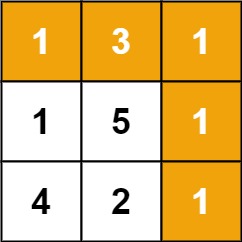
输入:grid = [[1,3,1],[1,5,1],[4,2,1]]输出:7解释:因为路径 1→3→1→1→1 的总和最小。
样例 2:
输入:grid = [[1,2,3],[4,5,6]]输出:12
提示:
- m == grid.length
- n == grid[i].length
- 1 <= m, n <= 200
- 0 <= grid[i][j] <= 200
分析:
- 面对这道算法题目,二当家的再次陷入了沉思。
- 这道题和62. 不同路径和63. 不同路径 II 有些类似,但是这次是寻找最优解,由于每个位置的数值不一定是多少,所以同样没法使用数学公式直接计算。
- 那么动态规划又成了此时的优选。
- 从左上角出发,网格的第一行的每个元素只能从左上角元素开始向右移动到达,网格的第一列的每个元素只能从左上角元素开始向下移动到达,此时的路径是唯一的,因此每个元素对应的最小路径和即为对应的路径上的数字总和。
- 其他的点只能从上或者从左到达,所以一个点的最优路径,一定经过上面或者左面。从上到下,从左到右开始动态规划,分解成了子问题。到达当前点的最短路径和,就是上面和左面点的最小路径和中的较小值加上当前点的值。
- 这里一样可以使用滚动数组优化空间。
题解:
rust:
impl Solution {pub fn min_path_sum(grid: Vec<Vec<i32>>) -> i32 {let (rows, cols) = (grid.len(), grid[0].len());let mut dp = vec![0; cols];dp[0] = grid[0][0];(1..cols).for_each(|c| {dp[c] = dp[c - 1] + grid[0][c];});(1..rows).for_each(|r| {dp[0] += grid[r][0];(1..cols).for_each(|c| {dp[c] = dp[c].min(dp[c - 1]) + grid[r][c];});});return dp[cols - 1];}
}
go:
func minPathSum(grid [][]int) int {rows, cols := len(grid), len(grid[0])dp := make([]int, cols)dp[0] = grid[0][0]for c := 1; c < cols; c++ {dp[c] = dp[c-1] + grid[0][c]}for r := 1; r < rows; r++ {dp[0] += grid[r][0]for c := 1; c < cols; c++ {if dp[c-1] < dp[c] {dp[c] = dp[c-1] + grid[r][c]} else {dp[c] += grid[r][c]}}}return dp[cols-1]
}
c++:
class Solution {
public:int minPathSum(vector<vector<int>>& grid) {const int rows = grid.size(), cols = grid[0].size();int dp[cols];dp[0] = grid[0][0];for (int c = 1; c < cols; ++c) {dp[c] = dp[c - 1] + grid[0][c];}for (int r = 1; r < rows; ++r) {dp[0] += grid[r][0];for (int c = 1; c < cols; ++c) {dp[c] = min(dp[c], dp[c - 1]) + grid[r][c];}}return dp[cols - 1];}
};
python:
class Solution:def minPathSum(self, grid: List[List[int]]) -> int:rows, cols = len(grid), len(grid[0])dp = [0] * colsfor c in range(cols):dp[c] = dp[c - 1] + grid[0][c]for r in range(1, rows):dp[0] += grid[r][0]for c in range(1, cols):dp[c] = min(dp[c], dp[c - 1]) + grid[r][c]return dp[cols - 1]java:
class Solution {public int minPathSum(int[][] grid) {final int rows = grid.length, cols = grid[0].length;final int[] dp = new int[cols];dp[0] = grid[0][0];for (int c = 1; c < cols; ++c) {dp[c] = dp[c - 1] + grid[0][c];}for (int r = 1; r < rows; ++r) {dp[0] += grid[r][0];for (int c = 1; c < cols; ++c) {dp[c] = Math.min(dp[c], dp[c - 1]) + grid[r][c];}}return dp[cols - 1];}
}
非常感谢你阅读本文~
欢迎【点赞】【收藏】【评论】三连走一波~
放弃不难,但坚持一定很酷~
希望我们大家都能每天进步一点点~
本文由 二当家的白帽子:https://le-yi.blog.csdn.net/ 博客原创~