63. 不同路径 II

题目链接：力扣

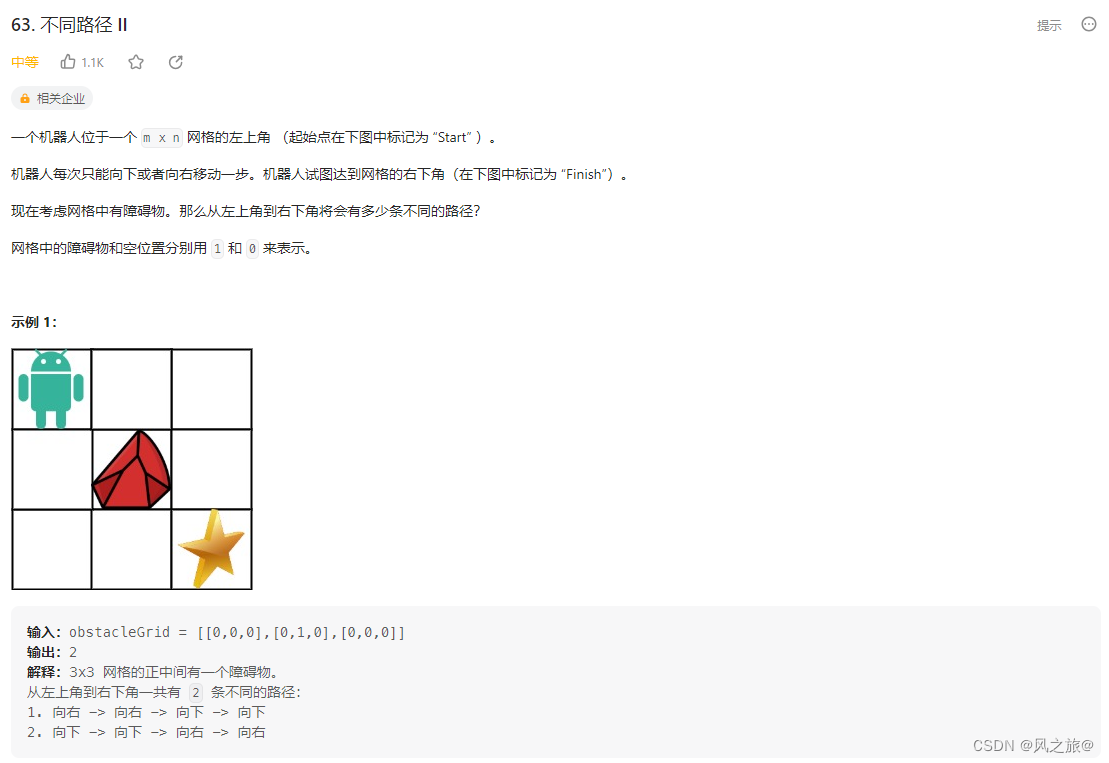解题思路：类似于 62. 不同路径

动态规划：

定义状态：对于m*n的网络，从最后一行到右下角，以及从最后一列到右下角，都只有一条不同路径：一直向右或一直向下，所以可以定义状态：dp[i][j]，表示从 (i,j) 到右下角的不同路径数量
初始状态和边界情况：
1. 根据状态的定义，最后一行以及最后一列达到右下角的路径都只有一种，但是如果有障碍物的话，障碍物以前的格子就到达不了右下角，障碍物后面的格子可以到达右下角。
  1. 所以，初始状态为：
    1. dp[m-1][i+1，...，n-1] = 1，dp[m-1][0，...，i]=0，(m-1，i)的位置有一个障碍物，如果这一行有多个障碍物，(m-1，i)是最右边的那个障碍物
    2. dp[i+1，...，m-1][n-1] = 1，dp[0，...，i][n-1]=0， (i，n-1)的位置有一个障碍物，如果这一列有多个障碍物，(m-1，i)是最下边的那个障碍物
确定状态转移：现在最后一行和最后一列的状态已经确定，其他的状态转移如下：
1. 根据状态的定义，从 (i,j) 到达右下角，有两种方案：
  1. 如果bstacleGrid[i][j] == 1，有障碍物，dp[i][j]=0
  2. 否则：dp[i][j] = dp[i+1][j]+dp[i][j+1]

AC代码：

class Solution {public static int uniquePathsWithObstacles(int[][] obstacleGrid) {if (obstacleGrid[0][0]==1){return 0;}int m = obstacleGrid.length;int n = obstacleGrid[0].length;int[][] dp = new int[m][n];int pos = n-1;boolean flag = true;for (;pos>=0;pos--){if (obstacleGrid[m-1][pos]==0&&flag){dp[m-1][pos] = 1;}else{flag = false;dp[m-1][pos] = 0;}}pos = m-1;flag = true;for (;pos>=0;pos--){if (obstacleGrid[pos][n-1]==0&&flag){dp[pos][n-1] = 1;}else{flag = false;dp[pos][n-1] = 0;}}for (int i = m - 2; i >= 0; i--) {for (int j = n - 2; j >= 0; j--) {if (obstacleGrid[i][j]==1){dp[i][j]=0;}else {dp[i][j] = dp[i+1][j]+dp[i][j+1];}}}return dp[0][0];}
}

上述算法的时间复杂度为O(mn)，空间复杂度为O(mn)

优化：在动态规划中，一般可以使用滚动数组进行空间优化，根据dp状态的定义，dp[i][j]只和dp[i+1][j]以及dp[i][j+1]相关，如下图所示：

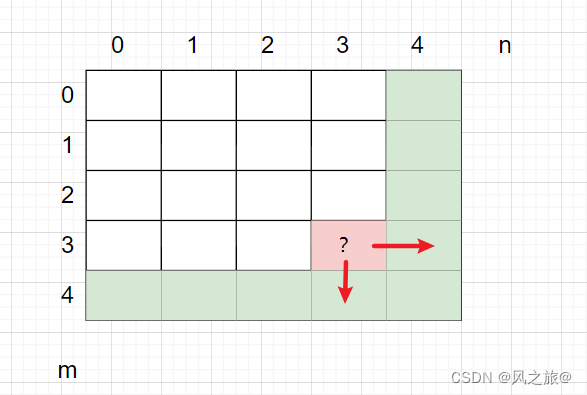
在求解二维dp数组中，先求解下面一行的dp数组（从右往左），然后再求解上面一行的dp数组(也是从右往左)，最终想要的目标是dp[0][0]，也就是最上面一行的dp数组值，当求解完第 i 行的dp值时，此时第 i+1行的dp值就不再需要了，所以只需要一维数组就可以完成更新，每次都是对这个一维数组进行滚动更新。具体如下：

int[] dp = new int[n]，用来保存每一行的dp值，初始时保存最下面一行的dp值，dp[n-1]=1（已经在右下角了，路径数量为1）
dp的更新过程：从最后一行往上更新(每一行中从右往左更新)
1. 如果 bstacleGrid[i][j] == 1，当前有障碍，显然从当前位置到达不了右下角，所以dp[j] = 0
2. 否则，如果 bstacleGrid[i][j] == 1 && j + 1 < n，此时dp[j] = dp[j] + dp[j+1]，
接下来分析为什么使用一维数组就可以完成二维更新：
1. 当在最后一行时
  1. bstacleGrid[i][j] == 1，dp[j] =0，比较容易理解，有障碍，到达不了
  2. 否则：dp[j] = dp[j]+dp[j+1]，因为数组在初始化时默认为0，所以在最后一行时(除dp[n-1]外)，相当于dp[j] = dp[j+1]，即从（m-1，j）到右下角的路径数量等于从（m-1，j+1）到右小角的数量，显然是符合要求的
2. 当求解倒数第二行时，此时dp[i]保存的是最后一行中每一列到右下角的路径数
  1. 如下如所示：
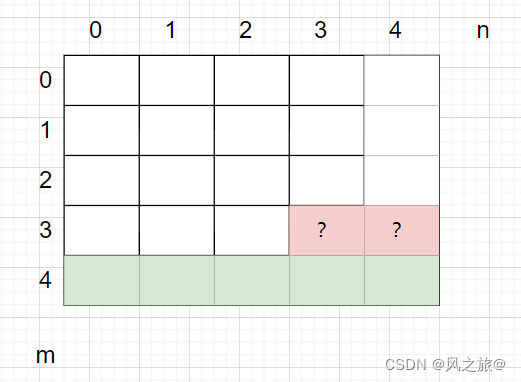
  2. 求解倒数第二行最后一个元素时，也就是(3,4)位置
    1. 如果bstacleGrid[3][4] == 1，dp[4] =0，比较容易理解，有障碍，到达不了
    2. 否则，因为是在最右边一列，只能向下走，所以（3,4）位置的dp值等于最后一行（4，4）位置的dp值，注意，在更新dp数组前，dp[3]保存就是（4，4）位置的dp值，所以不用更新，j+1 < n就是为了限制这种情况
  3. 求解倒数第二行的倒数第二个元素时，也就是(3,3)位置
    1. 如果bstacleGrid[3][4] == 1，dp[3] =0，比较容易理解，有障碍，到达不了
    2. 否则，可以向下走和向右走，那么此时(3,3)位置的dp值等于(3,4)位置的dp值加上(4,3)位置的dp值，因为此时dp[3]还没有更新，保存的就是(4，3)位置的dp值，而dp[4]已经更新了，保存的是(3,4)位置的dp值，所以可以直接dp[3]=dp[3]+dp[4]！可见使用一维数据的滚动更新就可完成二维数组的dp更新

AC代码：

class Solution {public static int uniquePathsWithObstacles(int[][] obstacleGrid) {if (obstacleGrid[0][0] == 1) {return 0;}int m = obstacleGrid.length;int n = obstacleGrid[0].length;int[] dp = new int[n];dp[n - 1] = 1;for (int i = m - 1; i >= 0; i--) {for (int j = n - 1; j >= 0; j--) {if (obstacleGrid[i][j] == 1) {dp[j] = 0;} else if (obstacleGrid[i][j] == 0 && j + 1 < n) {dp[j] = dp[j] + dp[j + 1];}}}return dp[0];}
}