👨🎓作者简介:一位即将上大四,正专攻机器学习的保研er
🌌上期文章:机器学习&&深度学习——图像分类数据集
📚订阅专栏:机器学习&&深度学习
希望文章对你们有所帮助
这篇文章的本意还是再一次复盘一下向量求导问题,很多时候的例子都直接推着就过去了,但是重新遇到总会卡壳一会,因为向量求导问题会分多种情况,所以我们在这里特意做个理解与总结。
向量求导问题
- 标量对列向量求导
- 列向量对标量求导
- 两个向量求导
- 向量链式法则
- 自动求导
- 计算图
- 自动求导的原理
- 正向累积和反向累积的对比
标量对列向量求导
已知列向量x:
x = [ x 1 , x 2 , . . . , x n ] T x=[x_1,x_2,...,x_n]^T x=[x1,x2,...,xn]T
将标量y对x进行求导,得到:
∂ y ∂ x = [ ∂ y ∂ x 1 , ∂ y ∂ x 2 , . . . , ∂ y ∂ x n ] \frac{\partial y}{\partial x}=[\frac{\partial y}{\partial x_1},\frac{\partial y}{\partial x_2},...,\frac{\partial y}{\partial x_n}] ∂x∂y=[∂x1∂y,∂x2∂y,...,∂xn∂y]
明明也就只有这么一个输出,而行表示输出,当然就是只有一行,而每列就代表每个偏导。
比如:对||x||2求导:
∂ y ∂ x = 2 x T \frac{\partial y}{\partial x}=2x^T ∂x∂y=2xT
或者y对<u,v>这个点积进行求导,u、v是关于x的向量,则:
∂ y ∂ x = u T ∂ v ∂ x + v T ∂ u ∂ x \frac{\partial y}{\partial x}=u^T\frac{\partial v}{\partial x}+v^T\frac{\partial u}{\partial x} ∂x∂y=uT∂x∂v+vT∂x∂u
列向量对标量求导
已知y是列向量,x是标量,那么y对x求导依旧是列向量。
毕竟y是列向量就已经说明了其具有多个输出,自然需要保证导数以后,输出的量依旧为那么多。
两个向量求导
这边要讲一下分子布局和分母布局的意义:
1、分子布局:分子为列向量,分母为行向量
2、分母布局:分子为行向量,分母为列向量
按照之前的想法来看,向量对向量求导,那么就先将y的每一行都对x求导,最后把每行的x拓展成多列的行向量,最终会得到一个矩阵。
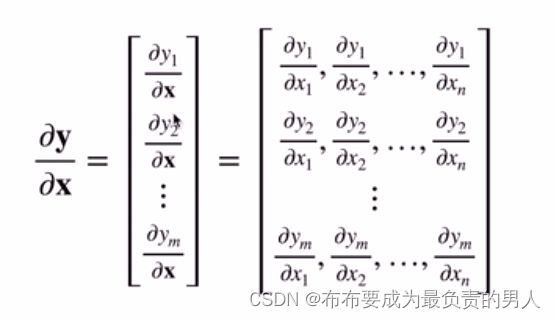
例如:
∂ x T A ∂ x = A T \frac{\partial x^TA}{\partial x}=A^T ∂x∂xTA=AT
我们的输入也可以拓展到矩阵,原理都一样
向量链式法则
我们从标量链式法则:
y = f ( u ) , u = g ( x ) 则 ∂ y ∂ x = ∂ y ∂ u ∂ u ∂ x y=f(u),u=g(x)则\frac{\partial y}{\partial x}=\frac{\partial y}{\partial u}\frac{\partial u}{\partial x} y=f(u),u=g(x)则∂x∂y=∂u∂y∂x∂u
拓展到向量:
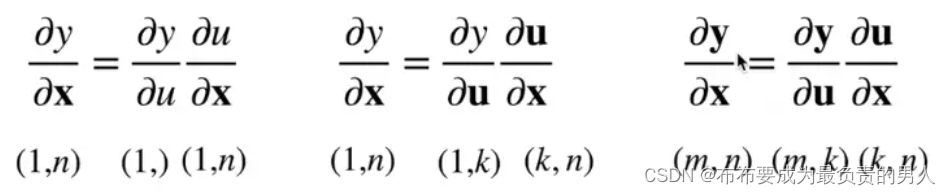
自动求导
计算图
将代码分解为操作子,将计算表示成一个无环图
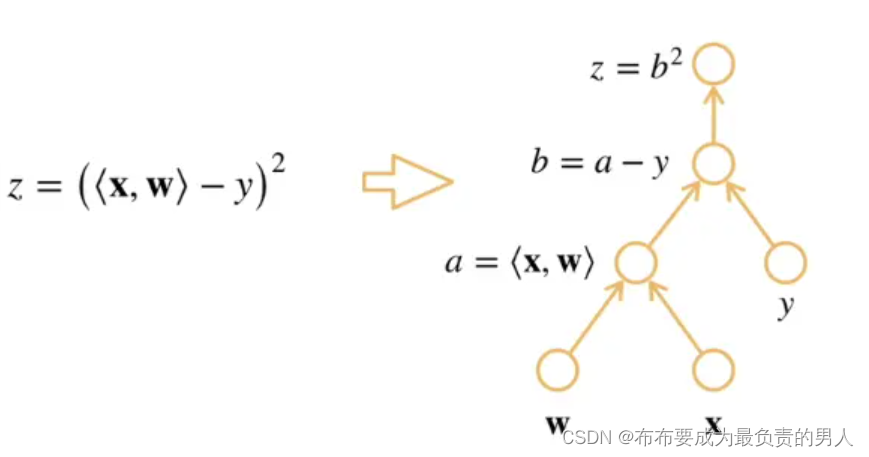
自动求导的原理
首先,有两种求导的方式,一种是从x开始求导,叫做正向累积,一种是从最上面的根结点开始向下求导,叫做反向累积也叫做反向传递。我们通常用反向累积

1、构造计算图
2、前向:执行图,存储中间结果(如下图b=a-y,a=<x,w>)
3、反向:从相反方向执行图(要去除不需要的枝)
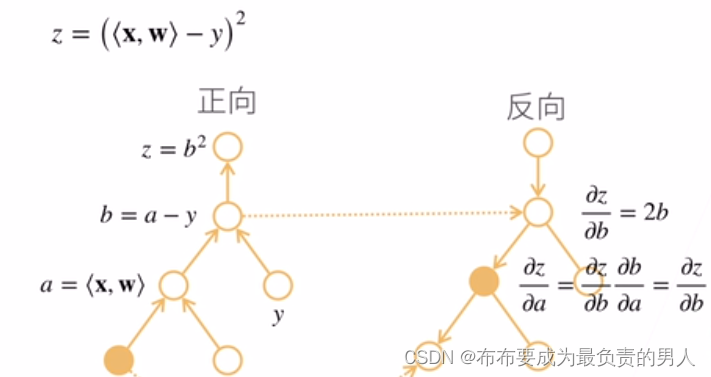
正向累积和反向累积的对比
对于我们常用的反向累积,他的计算复杂度是O(n),而内存复杂度是O(n),毕竟前向要走一遍来存储各个中间结果,所以需要耗费内存复杂度(这也就是为什么深度学习非常耗费GPU)。
而正向累积,计算复杂度是O(n),而内存复杂度是O(1),根本不需要存储中间结果,由下往上逐个求导即可。但是正向累积一般不使用,因为每次计算梯度都要扫一遍。