【GEE笔记】主成分分析（PCA）算法的实现和应用

前言

主成分分析（PCA）是一种常用的降维方法，它可以将多个相关的变量转换为少数几个不相关的变量，称为主成分（PC）。这些主成分可以反映原始变量的大部分信息，同时减少数据的复杂度和冗余性。在遥感领域，PCA可以用来提取影像的特征，消除噪声，增强对比度，或者进行分类和变化检测等。

本文介绍如何使用Google Earth Engine（GEE）平台实现PCA算法，并且展示一个应用案例，即利用PCA对哨兵二号（Sentinel-2）影像进行降维。

PCA算法原理

PCA算法的基本思想是通过正交变换，将原始数据投影到一个新的坐标系中，使得新坐标系的各个轴（即主成分）之间相互正交，且按照方差大小递减排序。这样，第一个主成分就是原始数据在最大方差方向上的投影，它包含了最多的信息；第二个主成分就是原始数据在次大方差方向上的投影，它包含了次多的信息；以此类推，直到所有的主成分都被提取出来。通常情况下，我们只需要保留前几个主成分，就可以达到较好的降维效果。

PCA算法的具体步骤如下：

对原始数据进行中心化处理，即每个变量减去其均值，使得新的数据集的均值为零。
计算原始数据的协方差矩阵，它反映了各个变量之间的线性相关程度。
对协方差矩阵进行特征值分解，得到特征值和特征向量。特征值表示了各个主成分的方差大小，特征向量表示了各个主成分的方向。
按照特征值的大小降序排列，选择前k个最大的特征值对应的特征向量作为新坐标系的基。
将原始数据乘以特征向量矩阵，得到新坐标系下的数据，即主成分。

GEE平台上的PCA实现

数据准备

定义了一个矩形区域作为研究区域

var geometry = ee.Geometry.Polygon([[[119.34885102549033, 36.519170262470254],[119.34885102549033, 36.32081057978827],[119.56583100595908, 36.32081057978827],[119.56583100595908, 36.519170262470254]]], null, false);

获取哨兵2影像，并对其进行一些预处理。选择2020年3月至5月期间，在哨兵2表面反射率（SR）影像集合中根据自定义的几何区域geometry进行裁剪。选择10个波段（B2, B3, B4, B5, B6, B7, B8, B8A, B11, B12），并对每个波段应用一个云掩膜函数，以去除云影响。然后均值合成为一幅图像。最后进行图像重采样，将空间分辨率转为统一的10米。以下是相关的代码：

var year = 2020
var bandlist = ['B2', 'B3', 'B4', 'B5', 'B6', 'B7', 'B8', 'B8A', 'B11', 'B12']
var start = ee.Date(year + '-3-01');
var finish = ee.Date(year + '-5-1');
var dataset = ee.ImageCollection('COPERNICUS/S2_SR').filterDate(start, finish).filterBounds(geometry).map(maskS2clouds)
var dataset10 = dataset.select(bandlist);
var bandsimage = dataset10.mean().clip(geometry)
print("输入影像", bandsimage)bandsimage = bandsimage.reproject('EPSG:4326', null, 10);
var scaledataset10 = bandsimage.projection().nominalScale();
var rgbVis = {min: 0.0,max: 3000,bands: ['B4', 'B3', 'B2'],
};
Map.centerObject(geometry, 12)
Map.addLayer(bandsimage, rgbVis, 'bandsimage');// 定义一个云掩膜函数
function maskS2clouds(image) {var qa = image.select('QA60');// Bits 10 and 11 are clouds and cirrus, respectively.var cloudBitMask = 1 << 10;var cirrusBitMask = 1 << 11;var mask = qa.bitwiseAnd(cloudBitMask).eq(0).and(qa.bitwiseAnd(cirrusBitMask).eq(0));return image.updateMask(mask).clip(geometry);
}

运行上述代码后，我们可以在地图上看到输入影像的真彩色显示，如下图所示：
在这里插入图片描述

PCA变换

接下来，实现PCA算法并将其封装为一个函数 doPCAandCR 。该函数的输入参数是一个多波段影像，输出参数是一个包含两个属性的对象: pcImage 和 cntributionRate 。 pcImage 是一个多波段影像，每个波段对应一个主成分分量， contributionRate 是一个数组，每个元素对应一个主成分的贡献率

PCA算法的主要步骤如下:

计算输入影像的每个波段的均值，并将其作为一个常数影像
将输入影像减去均值影像，得到中心化后的影像
将中心化后的影像转换为数组格式
计算数组的协方差知阵
对协方差知阵进行特征值分解，得到特征值和特征向量
将特征向量知阵与数组相乘，得到主成分数组
将主成分数组转换为影像格式，并按照波段顺序命名
将每个波段的特征值除以所有特征值之和，得到每个波段的贡献率

var result = doPCAandCR(bandsimage);
print("PCA", result.pcImage);
Map.addLayer(result.pcImage.select(0), {}, 'resultPCA1');
print("每个波段的贡献率", result.contributionRate);// 定义一个PCA和贡献率计算函数
function doPCAandCR(image) {// Get the band names of the imagevar bandNames = image.bandNames();var region = image.geometry();var meanDict = image.reduceRegion({reducer: ee.Reducer.mean(),geometry: geometry,scale: scaledataset10,tileScale: 16,maxPixels: 1e9});var means = ee.Image.constant(meanDict.values(bandNames));var centered = image.subtract(means);var arrays = centered.toArray();var covar = arrays.reduceRegion({reducer: ee.Reducer.centeredCovariance(),geometry: geometry,scale: scaledataset10,tileScale: 16,maxPixels: 1e9});var covarArray = ee.Array(covar.get('array'));var eigens = covarArray.eigen();var eigenValues = eigens.slice(1, 0, 1);var eigenVectors = eigens.slice(1, 1);var arrayImage = arrays.toArray(1);var principalComponents = ee.Image(eigenVectors).matrixMultiply(arrayImage);var sdImage = ee.Image(eigenValues.sqrt()).arrayProject([0]).arrayFlatten([getNewBandNames('sd', bandNames)]);var pcImage = principalComponents.arrayProject([0]).arrayFlatten([getNewBandNames('pc', bandNames)]).divide(sdImage);// 通过将每个波段的特征值除以所有特征值之和来计算每个波段的贡献率var sumEigenValues = eigenValues.reduce(ee.Reducer.sum(), [0]).get([0, 0]);var contributionRate = eigenValues.divide(sumEigenValues).project([0]);return { pcImage: pcImage, contributionRate: contributionRate };
}function getNewBandNames(prefix, bandNames) {var seq = ee.List.sequence(1, bandNames.length());return seq.map(function (b) {return ee.String(prefix).cat(ee.Number(b).int());});
}

将准备的数据进行主成分变换，得到各主成分及其贡献率，并将第一主成分可视化
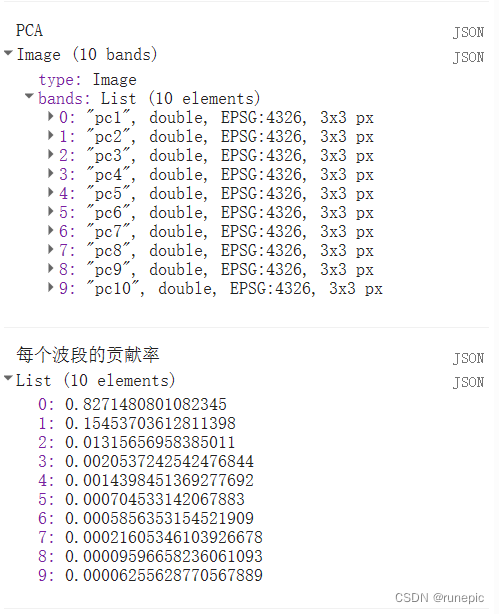
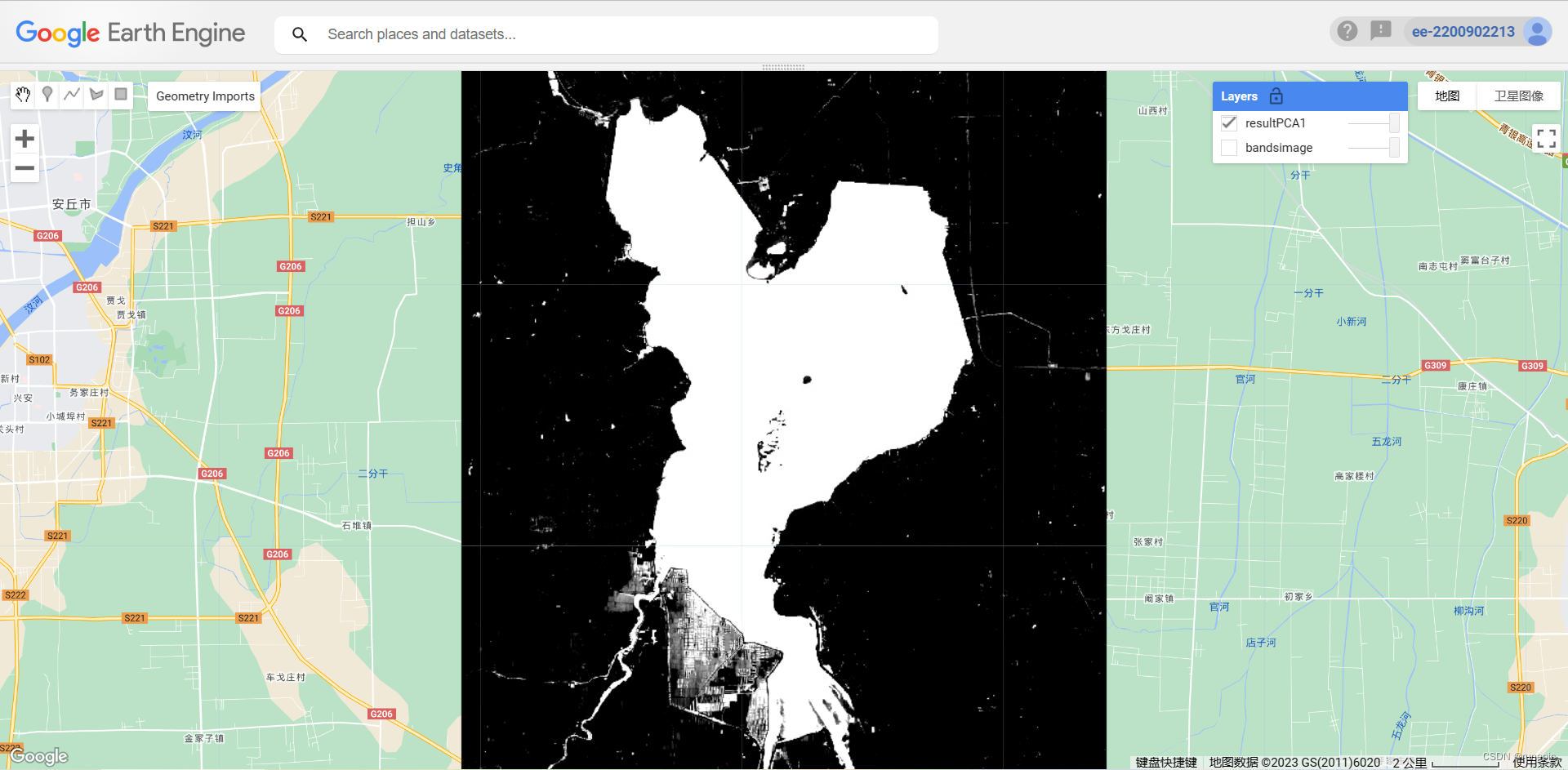
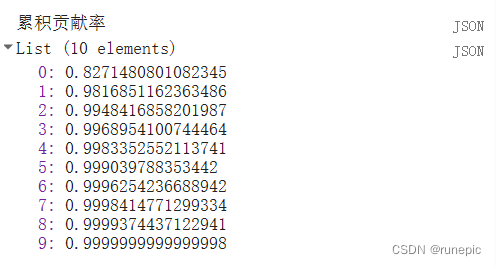
在这里插入图片描述

在这里插入图片描述

计算累积贡献率

// 对贡献率进行累加操作
var cumsum = ee.List(result.contributionRate.toList().iterate(accumulate, ee.List([])));
print("累积贡献率", cumsum);// 定义一个累加函数
function accumulate(value, list) {// 将list转换为ee.List对象list = ee.List(list);// 获取上一次的累加结果，如果没有则用0代替var previous = ee.Algorithms.If(list.size(), ee.Number(list.get(-1)), 0)//ee.Number(list.get(-1)).or(0);// 将当前值与上一次的结果相加var added = ee.Number(value).add(previous);// 返回更新后的listreturn list.add(added);
};