优化目标
相较于之前学习的线性回归和神经网络,支持向量机(Supprot Vector Machine,简称SVM)在拟合复杂的非线性方程的时候拥有更出色的能力,该算法也是十分经典的算法之一。接下来我们需要学习这种算法
首先我们回顾逻辑回归中的经典假设函数,如下图:
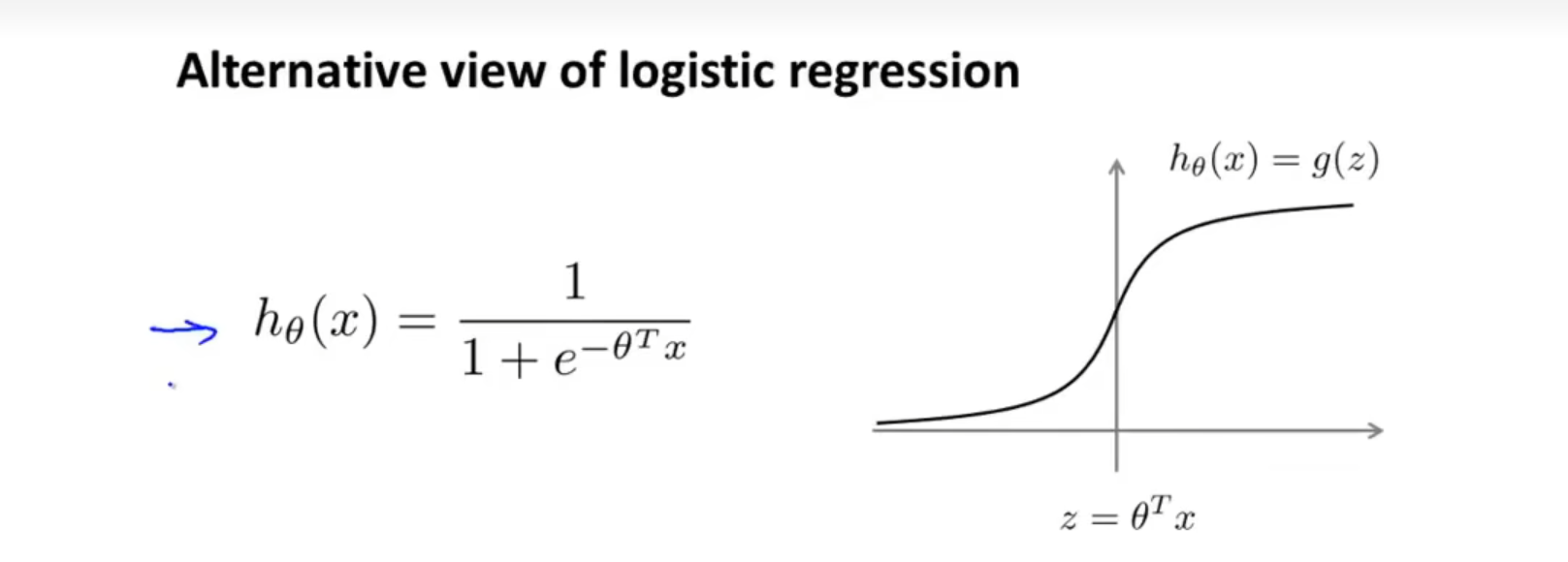
对于任意一个实例 ( x , y ) (x,y) (x,y),当y=1的时候,我们希望 h θ ( x ) ≈ 1 h_\theta(x)\approx1 hθ(x)≈1,也就是 θ T x > > 0 \theta^Tx>>0 θTx>>0;当y=0的时候,我们希望 h t h e t a ( x ) ≈ 0 h_theta(x)\approx0 htheta(x)≈0,也就是 θ T x < < 0 \theta^Tx<<0 θTx<<0。在这种情况下我们才认为算法预测正确了
在之前的学习中,我们了解到Logistics函数的方程如下:
逻辑回归
m i n θ 1 m [ ∑ i = 1 m y ( i ) ( − l o g h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) ( − l o g ( 1 − h θ ( x ( i ) ) ) ] + λ 2 m ∑ j = 1 λ θ j 2 \mathop{min}\limits_{\theta } \:\frac{1}{m} \left [ \sum_{i=1}^{m}y^{(i)}\left ( -log\:h_\theta (x^{( i)}) \right ) +(1-y^{(i)})\left ( -log(1-h_\theta (x^{(i)}) \right ) \right ]+\frac{\lambda }{2m}\sum_{j=1}^{\lambda }\theta _j^2 θminm1[i=1∑my(i)(−loghθ(x(i)))+(1−y(i))(−log(1−hθ(x(i)))]+2mλj=1∑λθj2
很明显,当y=1但是 h θ ( x ) ≈ 0 h_\theta(x)\approx0 hθ(x)≈0,或者y=0但是 h θ ( x ) ≈ 1 h_\theta(x)\approx1 hθ(x)≈1,因为这意味着逻辑回归的假设函数做出了错误的假设,代价函数应该狠狠地惩罚它
对比原来的逻辑回归,SVM的公式如下:
m i n θ C ∑ i = 1 m [ y ( i ) c o s t 1 ( θ T x ( i ) ) + ( 1 − y ( 1 ) ) c o s t 0 ( θ T x ( i ) ) ] + 1 2 ∑ j = 1 n θ j 1 \mathop{min}\limits_{\theta } C\sum_{i=1 }^{m}\left [ y^{(i)}cost_1(\theta ^Tx^{(i)})+(1-y^{(1)})cost_0(\theta ^Tx^{(i)}) \right ] +\frac{1}{2}\sum_{j=1}^{n}\theta _j^1 θminCi=1∑m[y(i)cost1(θTx(i))+(1−y(1))cost0(θTx(i))]+21j=1∑nθj1
很明显,前面的中括号是代价函数项,后面的是正则化项,在SVM中,使用参数 C C C来控制代价函数和正则化项之间的权重。
其中 c o s t 1 ( z ) cost_1(z) cost1(z)的图象是

c o s t 2 ( z ) cost_2(z) cost2(z)的图形是
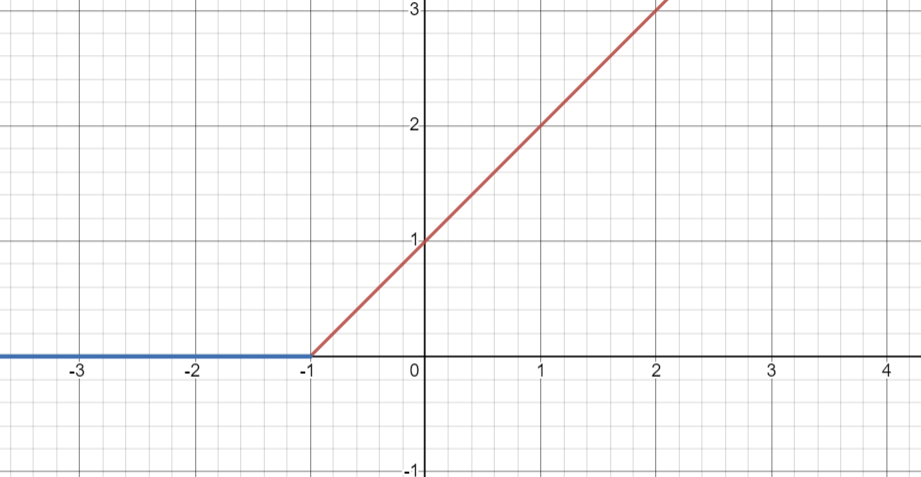
这意味着当y=1的时候,我们会希望 θ x T ≥ 1 \theta\:x^T\geq1 θxT≥1,才能使代价函数cost较小。而当y=0的时候,我们会希望 θ x ≤ − 1 \theta\:x\leq-1 θx≤−1。这样子我们在SVM的(-1,1)中建立了一个安全间距
大间距问题
对于一些间距较大的数据集,存在着多种划分方式,比如下面这种划分方式,虽然满足了条件,但是它的鲁棒性和泛化能力并出色

而下图这种划分方式显然比上面的好:划分边界和被划分的两个点集的距离是接近的,这个距离被称之为间距。显然,上图的划分方法间距就十分小,而下图的划分方式间距就比较大。
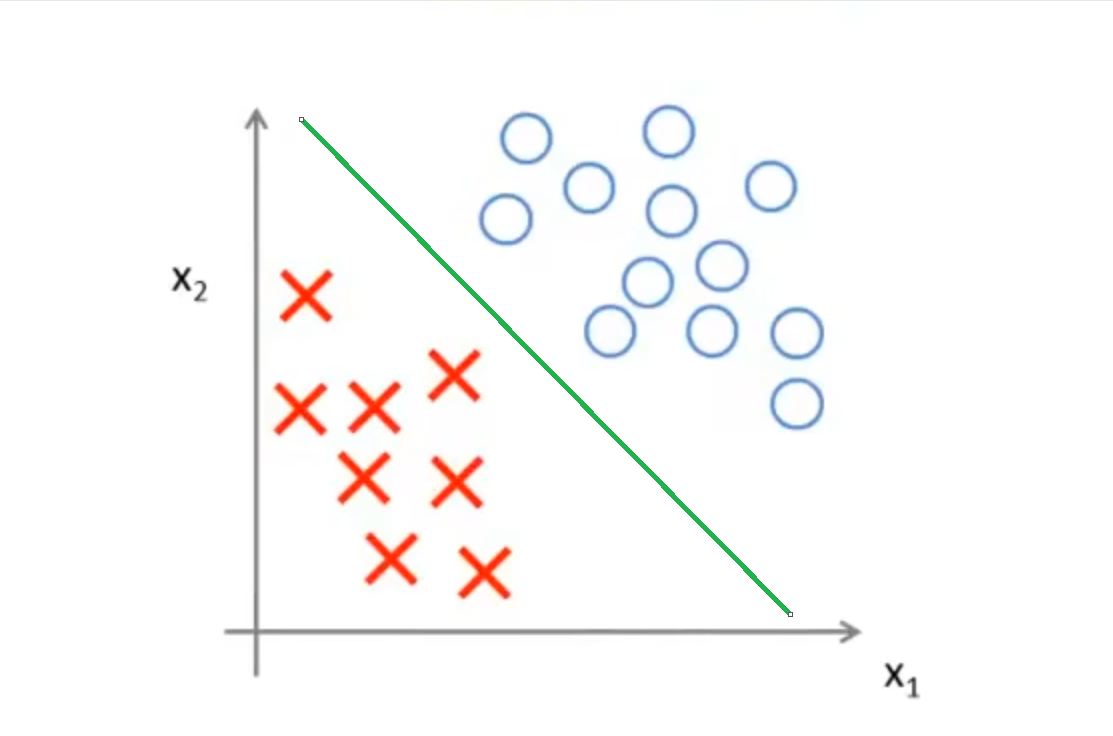
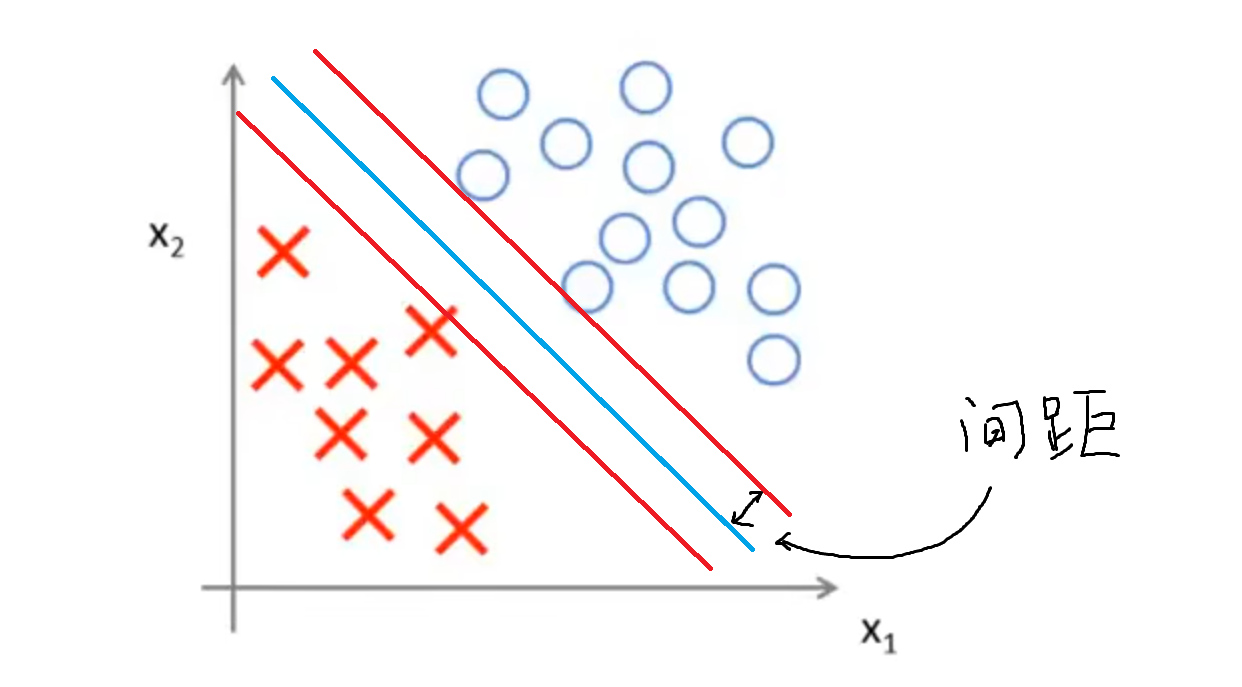
对于这些间距较大的数据集的划分,我们称之为大间距问题,而SVM可以很自然地处理大间距问题,将数据集划分成上图所示的样子,这使得SVM有优秀的鲁棒性,因此SVM有时候又称为大间距分类器。这也说明了SVM的划分方式:SVM会将点以最大间距进行分类。
注意:SVM在其参数C设置得十分大的时候会倾向于保持大间距,但是这会使得算法对异常点十分敏感
核函数
 注:$||w||$表示一个向量的长度
注:$||w||$表示一个向量的长度
假设在图上有三个点,分别是 l ( 1 ) l^{(1)} l(1), l ( 2 ) l^{(2)} l(2)和 l ( 3 ) l^{(3)} l(3),如下图所示

我们需要计算某个点x和着三个点的相似度,那么计算方法如下:
f 1 = s i m i l a r i t y ( x , l ( 1 ) ) = e x p ( − ∣ ∣ x − l ( 1 ) ∣ ∣ 2 2 σ 2 ) f_1=similarity(x,l^{(1)})=exp\left (-\frac{||x-l^{(1)}||^2}{2\sigma ^2}\right ) f1=similarity(x,l(1))=exp(−2σ2∣∣x−l(1)∣∣2)
f 2 = s i m i l a r i t y ( x , l ( 2 ) ) = e x p ( − ∣ ∣ x − l ( 2 ) ∣ ∣ 2 2 σ 2 ) f_2=similarity(x,l^{(2)})=exp\left (-\frac{||x-l^{(2)}||^2}{2\sigma ^2}\right ) f2=similarity(x,l(2))=exp(−2σ2∣∣x−l(2)∣∣2)
f 3 = s i m i l a r i t y ( x , l ( 3 ) ) = e x p ( − ∣ ∣ x − l ( 3 ) ∣ ∣ 2 2 σ 2 ) f_3=similarity(x,l^{(3)})=exp\left (-\frac{||x-l^{(3)}||^2}{2\sigma ^2}\right ) f3=similarity(x,l(3))=exp(−2σ2∣∣x−l(3)∣∣2)
其中 ∣ ∣ x − l ( i ) ∣ ∣ 2 ||x-l^{(i)}||^2 ∣∣x−l(i)∣∣2是x到 l ( 1 ) l^{(1)} l(1)的欧氏距离
上面所示的 s i m i l a r i t y similarity similarity函数是其中一种核函数,被称之为高斯核函数,可以写作 k ( x , l ( i ) ) = e x p ( − ∣ ∣ x − l ( i ) ∣ ∣ 2 2 σ 2 ) k(x,l^{(i)})=exp\left (-\frac{||x-l^{(i)}||^2}{2\sigma ^2}\right ) k(x,l(i))=exp(−2σ2∣∣x−l(i)∣∣2)
分析这个核函数,当 x ≈ l ( 1 ) x\approx l^{(1)} x≈l(1)的时候, ∣ ∣ x − l ( i ) ∣ ∣ 2 ≈ 0 ||x-l^{(i)}||^2\approx0 ∣∣x−l(i)∣∣2≈0,那么 k ( x , l ( 1 ) ) ≈ e x p ( 0 ) = 1 k(x,l^{(1)})\approx exp(0)=1 k(x,l(1))≈exp(0)=1;当x和 l ( i ) l^{(i)} l(i)距离很远的时候,由于其欧氏几何距离变得很大,那么 k ( x , l ( i ) ) = e x p ( − ∣ ∣ x − l ( i ) ∣ ∣ 2 2 σ 2 ) = e x p ( − L a r g e N u m b e r 2 σ 2 ) ≈ 0 k(x,l^{(i)})=exp\left (-\frac{||x-l^{(i)}||^2}{2\sigma ^2}\right )=exp\left (-\frac{Large Number}{2\sigma ^2}\right )\approx0 k(x,l(i))=exp(−2σ2∣∣x−l(i)∣∣2)=exp(−2σ2LargeNumber)≈0
接下来我们聚焦于参数 σ \sigma σ对整个核函数的影响,假设 l ( 1 ) l^{(1)} l(1)位于[3,5]

可以看到,当 σ \sigma σ比较小的时候,其图像变化的幅度更大;反之,其图像则比较平缓
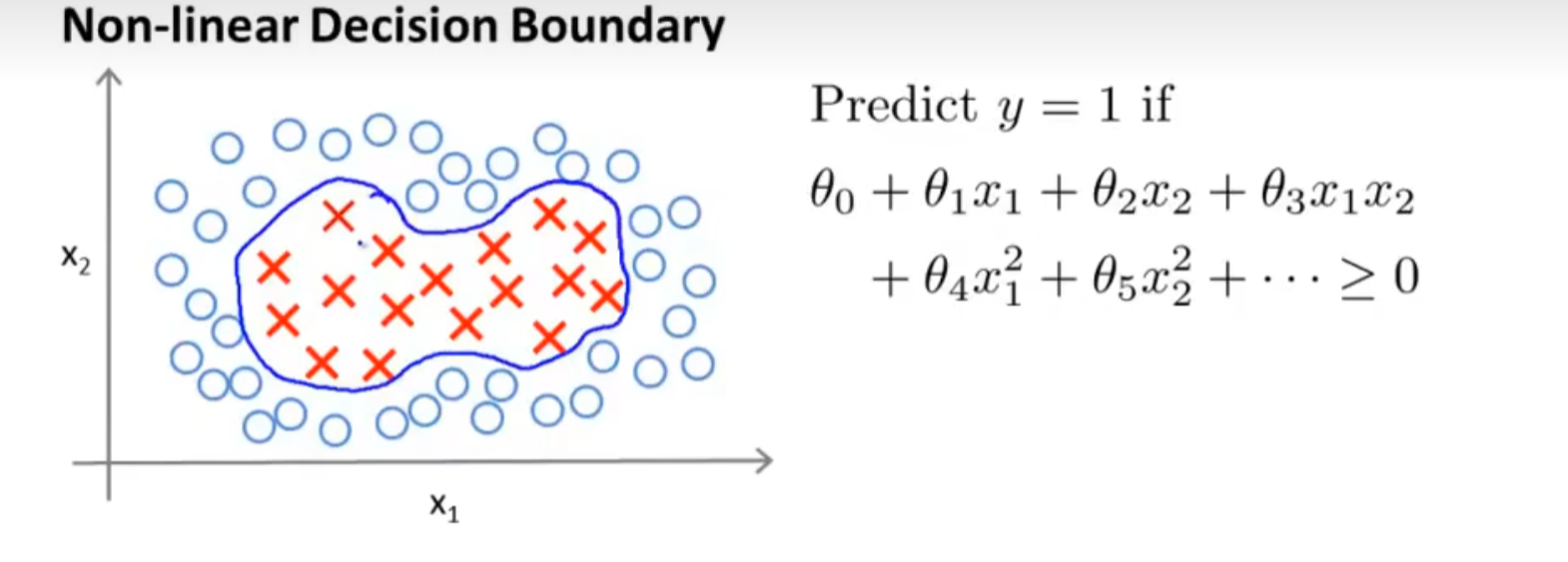
回到最初的图像,如果我们希望如果一个实例x靠近 l ( 1 ) l^{(1)} l(1)或者 l ( 2 ) l^{(2)} l(2)的时候,我们就预测其y=1(比如当一张图片上具有某些猫类的特征的时候,我们希望机器学习算法将其分类为猫)。那具体应该怎么做呢?

设定一个假设函数 f ( x ) = θ 0 + θ 1 f 1 + θ 2 f 2 + θ 3 f 3 f(x)=\theta_0+\theta_1f_1+\theta_2f_2+\theta_3f_3 f(x)=θ0+θ1f1+θ2f2+θ3f3,其中 f i = k ( x , l ( i ) ) f_i=k(x,l^{(i)}) fi=k(x,l(i)) 当 当 当f(x)\geq0 的时候,我们预测 y = 1 。并且令 的时候,我们预测y=1。并且令 的时候,我们预测y=1。并且令\theta_0-0.5, \theta_1=1,\theta_2=1,\theta_3=0$,那么会怎么样呢?
当x靠近 l ( 1 ) l^{(1)} l(1)的时候, f ( x ) = − 0.5 + 1 + 0 + 0 = 0.5 f(x)=-0.5+1+0+0=0.5 f(x)=−0.5+1+0+0=0.5,因此我们预测其y=1;而当x靠近 l ( 2 ) l^{(2)} l(2)的时候, f ( x ) = − 0.5 + 0 + 1 + 0 = 0.5 f(x)=-0.5+0+1+0=0.5 f(x)=−0.5+0+1+0=0.5,因此我们预测其y=1
神奇的来了,我们实际上可以画出一个非线性的边界(红线),在这个边界内 f ( x ) ≥ 0 f(x)\geq0 f(x)≥0,也就是意味着算法认为y=1

总而言之,通过高斯核函数可以衡量x到任意点的距离远近,而通过假设函数f(x)将若干个高斯核函数的计算集合在一块,规划出了一个非线性的边界。
使用SVM
现在已经很少人手搓SVM的 θ \theta θl了,正如很少人手搓一个数的平方根一样。但是在使用SVM的时候还是需要决定几个关键的参数。比如:
- 选择需要使用的参数C
- 选择SVM使用何种内核
比如不使用任何内核的SVM,称之为线性核函数。当你的实例拥有大量特征,但是训练集数量却不多的时候,可以使用线性SVM核函数来避免过拟合(此种情况也适合使用我们之前说的线性回归法)
另外一个策略是使用高斯核函数,上面已经介绍过了,高斯核函数如下:
f i = e x p ( − ∣ ∣ x − l ( i ) ∣ ∣ σ 2 ) , w h e r e l ( i ) = x ( i ) f_i=exp(-\frac{||x-l^{(i)}||}{\sigma ^2} ),where\:\: l^{(i)}=x^{(i)} fi=exp(−σ2∣∣x−l(i)∣∣),wherel(i)=x(i)这种情况下我们需要对参数 σ \sigma σ进行选择,如果 σ \sigma σ过小,那么得到一个高方差,低偏差的训练器;反之则是一个高偏差,低方差的训练器。当你的数据集数量很大,但是单个数据所拥有的特征量很少的时候,使用高斯核函数是一个不错的选择,因为它可以拟合出相当复杂的非线性决策边界
注意:使用高斯核函数之前,请对特征向量进行归一化,否则会导致在运算中各个特征向量权重不一致
除此之外,还有一些其他的核函数,此处只做简单介绍:
多项式核函数: k e r n a l ( x , l ) = ( x T l ) 2 kernal(x,l)=(x^Tl)^2 kernal(x,l)=(xTl)2x和l越靠近其内积越大
字符串核函数:用于处理文本的核函数
直方核函数
无监督学习
在无监督学习中,数据集不会含有对数据的标记,只包含数据的特征,也就是如下图:

我们可以看到Training Set中已经没有了 y y y,图上的点也没有了标记。而无监督算法的任务就是,找出这些点之间隐含的关系,比如说将上面的点集根据他们之间的距离分类为两个不同的集合。K-Means则是最广泛运用的聚类算法之一,接下来我们将会重点介绍它。
K-Means算法
以下图为例子:

假设我们想要将图上数据分类为两个簇,那么 我们首先要随机选取两个点作为聚类中心(一红一蓝),如下图所示:

接下来它们会重复做两件事:
- 簇分配
- 移动聚类中心
首先第一步是将各个点分配给簇。对于任意一个点,检查两个聚类中心和该点的距离,并且将点分配给距离较短的簇,分配的结果如下所示

接下来则是移动聚类中心,对于红聚类中心,我们计算所有红色点的横坐标平均值x1和纵坐标平均值y1,并且将红聚类中心移动到 ( x 1 , y 1 ) (x_1,y_1) (x1,y1)处,对蓝聚类中心也进行同样的处理,可得到如下效果:
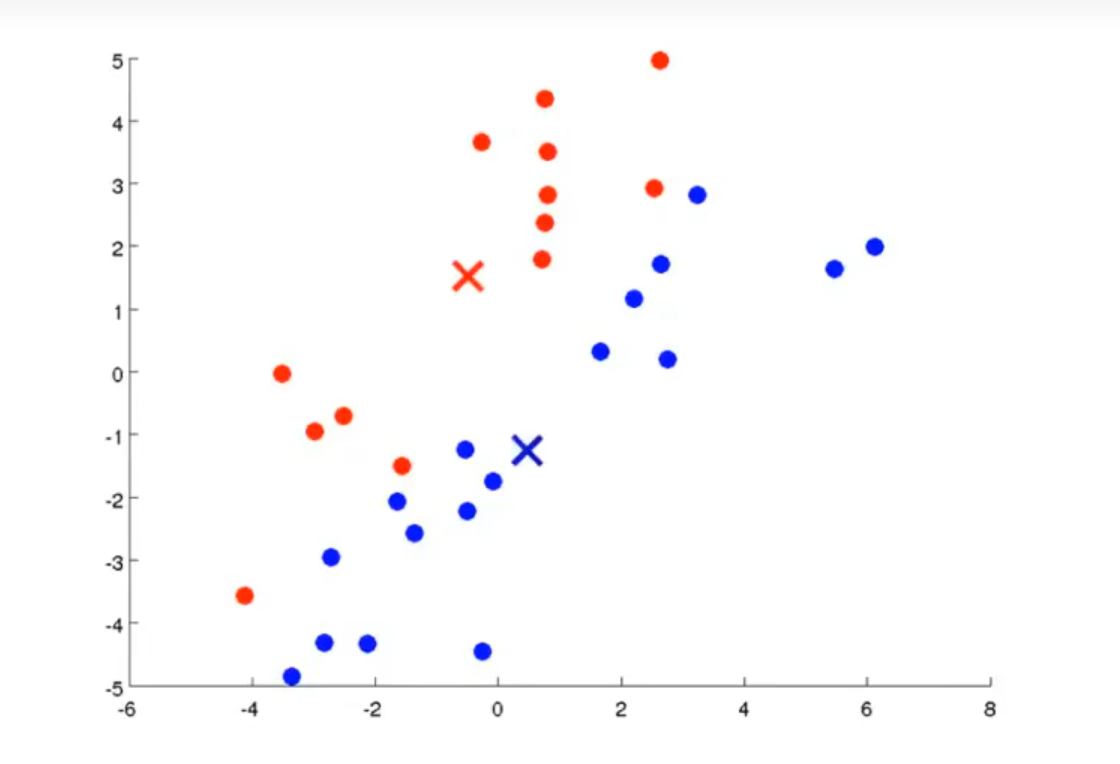
重复上述步骤若干次,会得到如下结果

此时所有数据都被分类完毕,而且再继续进行迭代,聚类中心也不会发生移动,此时我们认为K-Means已经聚合了。
接下来我们总结一下更加普遍的K-Means算法的执行流程:
输入:
- 整数参数K:表示需要分为K个簇
- 训练数据集 x ( 1 ) , x ( 2 ) , x ( 3 ) . . . x ( m ) , {x^{(1)},x^{(2)},x^{(3)}...x^{(m)},} x(1),x(2),x(3)...x(m),
- 随机初始化K个聚类中心 μ 1 , μ 2 . . . μ K \mu_1,\mu_2...\mu_K μ1,μ2...μK
- 重复迭代如下步骤:
- 对于 x ( i ) , i ∈ ( 1 , m ) x^{(i)},\:i\in(1,m) x(i),i∈(1,m),求离 x ( i ) x^{(i)} x(i)最近的聚类中心 μ ( j ) \mu^{(j)} μ(j),并且将点 x ( i ) x^{(i)} x(i)归为簇 c ( j ) c^{(j)} c(j)
- 对于 μ ( k ) , k ∈ ( 1 , K ) \mu^{(k)},\:k\in(1,K) μ(k),k∈(1,K),求簇 c ( k ) c^{(k)} c(k)中所有点的均值,并且将 μ ( k ) \mu^{(k)} μ(k)移动到该点
有意思的是,哪怕某个数据集中的数据没有明显的边界,聚类算法依旧能进行一定的划分,比如对于衣服尺寸和身高的数据集
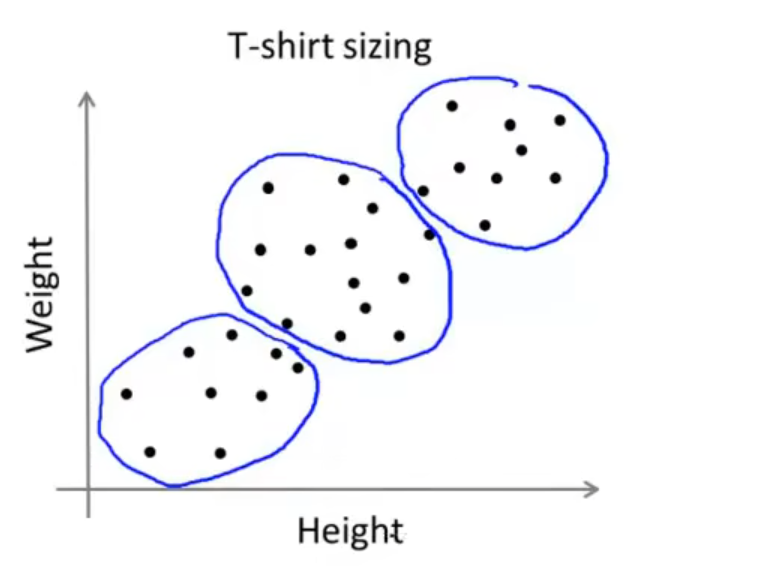
K-Means的优化目标函数
优化目标函数能够确保K-Means算法最终得到的结果最佳,确保算法运行正确,也可以用于帮助K-Means避免局部最优解,开始之前,我们先规定几个符号:
- c ( i ) c^{(i)} c(i):表示实例 x ( i ) x^{(i)} x(i)所属的簇
- μ ( k ) \mu^{(k)} μ(k):表示第k个簇的聚类中心
- μ c ( i ) \mu_c^{(i)} μc(i):表示实例 x ( i ) x^{(i)} x(i)所属的聚类中心
那么其优化目标函数为:
J ( c ( 1 ) . . . c ( m ) , μ 1 . . . μ k ) = 1 m ∑ i = 1 m ∣ ∣ x ( i ) − μ c ( i ) ∣ ∣ 2 J(c^{(1)}...c^{(m)},\mu_1...\mu_k)=\frac{1}{m}\sum_{i=1}^{m} ||x^{(i)}-\mu_c^{(i)}||^2 J(c(1)...c(m),μ1...μk)=m1i=1∑m∣∣x(i)−μc(i)∣∣2
式子后面的 ∣ ∣ x ( i ) − μ c ( i ) ∣ ∣ 2 ||x^{(i)}-\mu_c^{(i)}||^2 ∣∣x(i)−μc(i)∣∣2表示的是实例 x ( i ) x^{(i)} x(i)到其所属的簇的聚类中心的距离的平方
而我们需要做的是改变 c ( 1 ) . . . c ( m ) c^{(1)}...c^{(m)} c(1)...c(m)和 μ 1 . . . μ k \mu_1...\mu_k μ1...μk的值,使得 J ( c ( 1 ) . . . c ( m ) , μ 1 . . . μ k ) J(c^{(1)}...c^{(m)},\mu_1...\mu_k) J(c(1)...c(m),μ1...μk)最小
随机初始化
在初始化聚类中心的时候,上文只提到了随机选取若干个点作为聚类中心