D.The Game of Eating

贪心

 

题目说每个人只关心自己享用的菜肴,而不考虑他人,每个人的目标都是使得自己喜欢的菜肴尽可能多

也就是说每个人都很鸡贼,它们当下都是做出最有利于自己的选择,对于某一个人,他首先会算在他之后他最喜欢的菜是否会被选择,如果会被选择,那么他就不选自己最喜欢的菜,然后再看次喜欢的菜,看是否会被选,以此类推,直到发现后面没人选时,他才会选,这样当k个菜都选完时,他喜欢的菜的数量可以达到最大,每个人都会这么想,按这样的话,对于最后一个选菜的人,他自己最喜欢的菜如果没人选的话,他自己肯定会选,所以前面的人算到最后一个人会选,所以前面的人故意不选这道菜,最后只能让最后一个人选这道菜,所以倒过来贪心即可

AC代码：

#include<iostream>
#include<algorithm>
#include<cstring>
#define endl '\n'
using namespace std;
const int N=2010;
int a[N][N];
int flag[N];
void solve()
{int n,m,k;cin>>n>>m>>k;memset(flag,0,sizeof flag);for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>a[i][j];}}//从第一个人开始选菜,一人选一道菜,一共选k道菜,现从k往前遍历for(int i=k;i;i--){int t=(i-1)%n+1;//选第i道菜轮到了编号为t的人int x=0;for(int j=1;j<=m;j++){if(!flag[j]&&a[t][j]>a[t][x]) x=j;}flag[x]=1;}for(int i=1;i<=m;i++){if(flag[i]) cout<<i<<" ";}cout<<endl;
}
int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t;cin>>t;while(t--)solve();return 0;
}

E.square 

题意是找到一个y(大于等于x),使得x是y的平方的前缀(前缀的位数只有可能是1到9,因为x最大才1e9,所以只需要枚举一下10的幂,i从0到9)

(y^2)/(10^i)=x -->x*10^i<=y^2,所以要保证y^2大于等于x*10^i,如果y^2小于x*10^i的话,x不可能是y^2的前缀的

然后如果y的平方的前缀是x的话(先将x,y^2分别转为字符串并存储,取y^2字符串的前x位和字符串x比较是否相等),那么就符合

比如说x=12,x*10=120,sqrt(x*10)=10,10*10小于120,不可能

11*11=121,发现可以

x*100=1200,sqrt(x*100)=34,34*34小于1200,不可能

35*35=1225,发现可以,然后35*35=1296,发现也可以

说明要想可以,首先得保证y^2大于等于x*10^i,然后从符合条件最小的y开始找,如果y符合,后面可能还有符合的y,但是最小的y不符合,那么后面就更不可能符合了,因为比如说x为12,然后x*10^i,某个最小的y,y^2的前两位是13,已经不符合前缀12了,所以y更大的话就更不可能符合前缀12了

法一:

 AC代码：

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<vector>
#include<cmath>
using namespace std;
typedef long long LL;
LL solve()
{LL x;cin>>x;if(x==0) return 0;string xx=to_string(x);string s;int len=xx.size();int res=-1;for(int i=0;i<10;i++){LL y=sqrt(x*pow(10,i));if(y*y<x*pow(10,i)) y++;s=to_string(y*y);if(s.substr(0,len)==xx) return y;}return res;
}
int main()
{int t;cin>>t;while(t--)cout<<solve()<<endl;return 0;
}

法二:

AC代码：

#include <iostream>
#include <cmath>
#define int long long
using namespace std;
int solve()
{int x;cin>>x;int z=x+1;int y;int flag=0;//最多循环10次,为了保证x不超出long long范围,从而导致溢出,发生错误for(int i=0;i<10;i++){y=sqrt(x*pow(10,i));//这边改成y*y<pow(10,i)而不是y*y!=pow(10,i),因为pow有精度问题,可能数太大了开根号不一定会下取整,可能上取整if(y*y<x*pow(10,i)) y++;//如果y*y大于等于x*10的幂并且y*y小于(x+1)*10的幂if(y*y>=x*pow(10,i)&&y*y<z*pow(10,i)){flag=1;break;}}if(flag==1) return y;else return -1;
}
signed main()
{int t;cin>>t;while(t--)cout<<solve()<<endl;;return 0;
}

K.Box

AC代码：

#include<iostream>
#include<algorithm>
#include<cstring>
#define int long long
using namespace std;
const int N=1e6+10;
int f[N][3];
//只需考虑当前枚举到的i是否有盖子,以及它的盖子左移,还是它的前一个盖子右移
//f[i][0]表示当前状态没有盖子,本来就没有盖子也有可能是把盖子给了左边,1到i获得的最大分数
//f[i][1]表示当前状态有盖子,而且是本来就有盖子,1到i获得的最大分数
//f[i][2]表示当前状态有盖子,但是是左边给了它盖子,1到i获得的最大分数
int a[N],b[N];
int n;
void solve()
{cin>>n;for(int i=1;i<=n;i++) cin>>a[i];for(int i=1;i<=n;i++) cin>>b[i];for(int i=1;i<=n;i++){//如果当前有盖子if(b[i]){//f[i][0]表示i没盖子,所以需要把i的盖子左移,f[i-1][0]表示i-1没盖子,1到i-1获得的最大分数,//然后加上a[i-1]即为f[i][0],1到i获得的最大分数f[i][0]=f[i-1][0]+a[i-1];//f[i][1]表示i当前状态有盖子,而且是本来就有盖子,所以前面i-1三种状态只需取最大值即可,再加上a[i]f[i][1]=max({f[i-1][0],f[i-1][1],f[i-1][2]})+a[i];}//如果当前没有盖子else {//只要取i-1三种状态最大的就行f[i][0]=max({f[i-1][0],f[i-1][1],f[i-1][2]});}//如果前一个有盖子,这个情况单独考虑,因为把前一个盖子右移,就不需要考虑当前位置有无盖子了//f[i][2]表示当前状态有盖子,但是是左边给的盖子,可以是前面i-1本来就有盖子,然后将盖子右移,导致自己没有盖子了,也可以是//前面i-1本来就有盖子,然后将盖子右移,但是i-2的盖子又给了i-1if(b[i-1]) f[i][2]=max(f[i-1][1]+a[i]-a[i-1],f[i-1][2]+a[i]);}cout<<max({f[n][0],f[n][1],f[n][2]})<<endl;
}
signed main()
{solve();return 0;
}

I.Link with Gomoku 

五子棋,双方博弈,轮流下,首先得保证双方数量相等或者差一个(这很关键)

然后就是保证横着竖着斜着不能有连续5个相同

行数为0到n-1,列数为0到m-1

可以以4行为1个循环,前两行偶数列放o,奇数列放x,后两行偶数列放x,奇数列放o(这样的好处是不需要管列数是奇数还是偶数,在一行中数量是相当的)

最后要保证双方数量相等或者差一个,需要在最后特殊处理一下,如果n%4得到完整的k个4行后还有几行,如果还有一行,那么数量相当,不需要考虑,如果还有三行

 

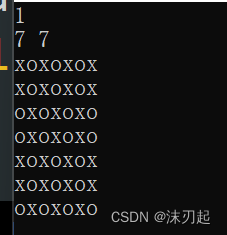
如图,x会比o多一个,所以也不要考虑

所以只需要考虑还有两行的情况,只要将最后一行反置就行

AC代码： 

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=1e3+10;
char s[N][N];
int n,m;
void solve()
{cin>>n>>m;for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(i%4<2){if(j&1) s[i][j]='o';else s[i][j]='x';}else{if(j&1) s[i][j]='x';else s[i][j]='o';}}}if(n%4==2){for(int j=0;j<m;j++){if(j&1) s[n-1][j]='x';else s[n-1][j]='o';}}for(int i=0;i<n;i++){for(int j=0;j<m;j++){cout<<s[i][j];}cout<<endl;}
}
signed main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t;cin>>t;while(t--)solve();return 0;
}