线性代数矩阵乘法用C++代码实现，再也不用担心算错啦！

news/2025/1/16 4:47:27/

c++实现矩阵相乘

- 矩阵乘法的定义
- 矩阵相乘的代码
- 完整的程序
- 实现线代其它操作的参考链接

线性代数矩阵相乘一旦阶数多了算的可真是让人CPU疼，但可爱的计算机是不怕累又超听话，所以用一个c++程序帮助你轻松解决矩阵相乘！！

矩阵乘法的定义

设A为m * n的矩阵，B为n * p的矩阵，那么称m * p的矩阵C为矩阵A与B的乘积，记作C=AB ，其中矩阵C中的第i行第j列元素可以表示为：
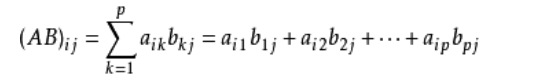
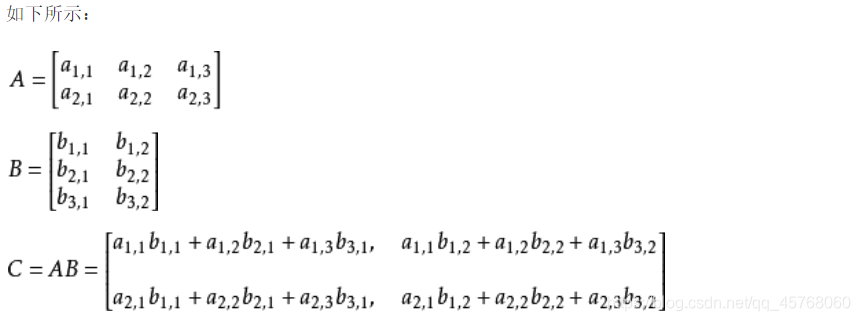
在这里插入图片描述

矩阵相乘的代码

这个算法很简单，直接利用矩阵相乘的定义及运算法则即可：
话不多说了，直接上代码：

vector<vector<double> > multiply(vector<vector<double> > matrix1,vector<vector<double> > matrix2)
{   if(matrix1[0].size()!=matrix2.size()){cout<<" 这两个矩阵不能相乘";exit(1);}int n = matrix1.size(),m=matrix2[0].size();int l =matrix2.size();vector<vector<double> > matrix3(n);for(int i=0;i<n;i++)for(int j=0;j<m;j++){   double t =0;//执行一次相乘for(int k=0;k<l;k++){t+=matrix1[i][k]*matrix2[k][j];}matrix3[i].push_back(t);}return matrix3;
}

完整的程序

给出完整的程序去供直接使用

#include<bits/stdc++.h>
using namespace std;
vector<vector<double> > multiply(vector<vector<double> > matrix1,vector<vector<double> > matrix2)
{   if(matrix1[0].size()!=matrix2.size()){cout<<" 这两个矩阵不能相乘";exit(1);}int n = matrix1.size(),m=matrix2[0].size();int l =matrix2.size();vector<vector<double> > matrix3(n);for(int i=0;i<n;i++)for(int j=0;j<m;j++){   double t =0;for(int k=0;k<l;k++){t+=matrix1[i][k]*matrix2[k][j];}matrix3[i].push_back(t);}return matrix3;
}
void output(vector<vector<double> > det)
{int m=det.size(),n=det[0].size();for(int i=0;i<m;i++){for(int j=0;j<n;j++)cout<<det[i][j]<<"  ";cout<<endl;}
}
int main()
{   int n1,m1;cout<<"Enter matrix1(n1*m1) n1,m1:";cin>>n1;cin>>m1;vector<vector<double> > matrix1(n1);//初始化det1为n1行 for(int i=0;i<n1;i++)for(int j=0;j<m1;j++){double t;cin>>t;matrix1[i].push_back(t); }int n2,m2;cout<<"Enter matrix2(n2*m2) n2,m2:";cin>>n2;cin>>m2;vector<vector<double> >matrix2(n2);//初始化det1为n1行 for(int i=0;i<n2;i++)for(int j=0;j<m2;j++){double t;cin>>t;matrix2[i].push_back(t); }output(multiply(matrix1,matrix2));}