文章目录
- 考试要求
- 考试内容
- 简单复习
- 插值
- 拟合和回归
- 数值积分
- 直接法
- 迭代法
- 非线性方程求根
- 微分方程数值解
- 去年考题
- 第一题,插值(12分)
- 第二题,回归和拟合
- 第三题,数值积分
- 第四题,线性方程组求解
- 第五题,非线性
- 第六题,微分方程求数值解
- 总结
考试要求
- 两个小时,开卷,可用计算器
- 开卷:全开卷,可以多张A4纸,但是不能看电子版的资料
- 范围:1-9章。
- 题型:6个大题
考试内容
- 有效数字
- 根据条件做多项式插值和误差估计:
- 一定是埃尔米特插值,能够写出插值多项式,以及相关误差。12分
- 拟合和回归
- 最小二乘做拟合,极大似然做回归
- 数值积分:数值积分公式的构造和代数精度,给你一个不完整的数值积分公式,确定构造公式,然后确定代数精度。
- N-C公式,只要求掌握梯形公式和simpson公式
- 复化公式(一般是复化梯形公式(二等分)和复化Simpson公式)
- 高斯公式(两个点的高斯公式)
- 线性方程组:
- LU分解(Doolittle分解),J方法和GS方法的计算:给你初值X0,你用对应方法迭代一次
- 收敛性的判定
- Richardson迭代,参数选取,对于任意初值都收敛的值,以及最优值得选取
- 非线性方程求根:
- 基本迭代法得构造,给出非线性方程,要能构造两种收敛格式,判断其收敛性并比较其收敛速度。
- 微分方程的求解:
- 解析解:给出一阶线性微分方程,要会用积分因子法或者分离变量法去求解析解
- 数值解:显示欧拉,隐式欧拉和改进欧拉
简单复习
插值
给你一个包含导数插值点,然后能过够列出对应插值公式,可以用Lagrange插值或者Newton插值实现,但是一定是Hermite插值的类型,最后要能够估计误差。
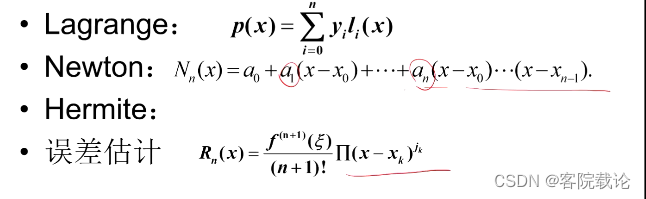
拟合和回归
- 拟合:直接用线性最小二乘,要列清楚具体流程,一定要出现矩阵的转置乘以系数矩阵的那一步 。不用法方程进行求解。

- 回归:极大似然估计,说明情况后,写出对应的似然函数,求出似然函数的最大值点。
- 需要说明:
- 总体分布规律已知,随机项是零均值,同方差,正态分布的假设下,才能得到整体的分布规律是正态。
- 分布参数未知

数值积分
- 公式构造:给你一个不完整的数值积分公式,如何选参数,使其具有尽可能高的代数精度,将被积函数一次带入x的零次方,一次方,二次方等,测试其满足条件的代数精度。
- N-C公式:仅考n=1和n=2
- 复化公式:仅考二等分的复化梯形公式和复化Simpson公式(少考)
- 高斯公式:只靠两个点的Gauss公式

直接法
- 直接考Doolittle分解,先将A分解成单位下三角和上三角的乘积。

迭代法
- 三个基本迭代法,都考
- 收敛性:记住使用严格对角占优性进行判定

非线性方程求根
- 仅考不动点迭代,要回判断收敛性和收敛速度。
- 收敛性:只需要满足局部收敛,根的位置局部连续并且的导数的绝对值小于1
- 如果给了一个初值,需要判断对初值是否收敛的。
- 尤其是对于重根的处理,需要注意。
- 构造两种,一种可以选择牛顿迭代。

微分方程数值解
- 解析解要会求:要会用积分因子法或者分离变量法去求解析解
- 三种欧拉都会考到

去年考题
- 今年考题和去年类似,强烈建议把去年的题目做一遍。
第一题,插值(12分)

- 今年,四个插值条件改变了其他都是一样的。


第二题,回归和拟合
- 同去年,今年老师说就是换了一个表,弄清楚流程即可

- 今年,改变了表格,有可能会多一小问。

第三题,数值积分
- 不完整的数值积分公式,需要确定对应A1,A2和x1的值,使其代数精度尽可能高,并指出代数精度,需要注意定积分的范围。
- 两个点的高斯公式,需要对区间进行定积分的替换,保证区间范围为【-1,1】
- 牛顿科特斯公式,根据精度,确定需要几个点进行计算。
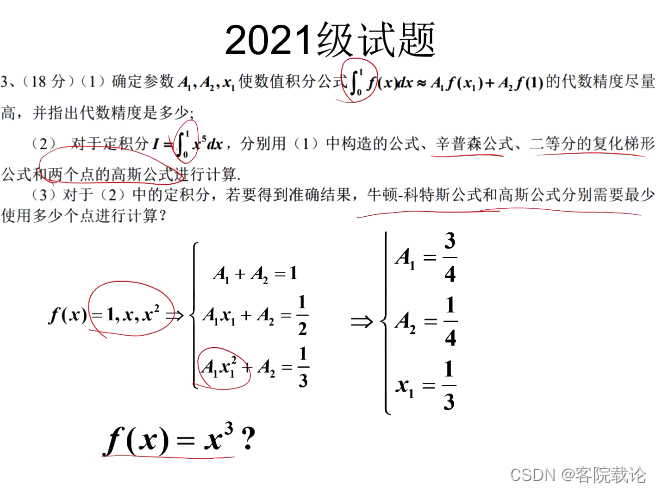
- 今年,改变了积分的公式和计算方式。

第四题,线性方程组求解

- 第一小问,做doolittle分解,求解线性方程组,将A分解成单位下三角,一定要有这个过程,不然没有过程分。
- 第二小问,从初值出发,分别用Jacobi迭代和G-S迭代一步。对角占优性和对称正定性的判断,重点在于一个对称矩阵是否为正定的。
- 第三问,三个特征值求出来,三个特征值为7,5,1。根据结果进行判定α的结果。
- 第四问,不考,今年没讲,所以分值会少一点
- 注意:今年的题目,LU分解过程中,Y或者L或者U的过程可能是分数,需要在这些过程中保留分数的结果。尽量不要使用计算器,否则会越来越复杂,计算结果保留最简分数和根号。
- 今年仅仅改变了线性方程组,前三问相同。


第五题,非线性

- 重根计算,可以使用牛顿迭代,然后使用修改之后的牛顿迭代(乘以n),收敛速度更快。今年不一定考重根。
- 今年仅仅改变了方程的区间。

第六题,微分方程求数值解

- 第一问,求解析解
- 第二问,算出了近似值,然后知道了准确值,来比较有效数字。判断两种方法的有效数字。
- 今年仅仅修改了微分方程。


总结
- 今年是六道大题,题型和去年相似

![[cpp进阶]C++智能指针](https://img-blog.csdnimg.cn/3f718a199e3d4f178a6a265266731a67.png)