( 链表) 142. 环形链表 II——【Leetcode每日一题】

❓142. 环形链表 II

难度：中等

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

示例 1：

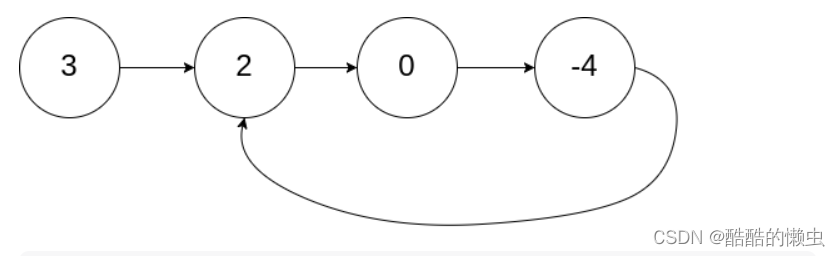
在这里插入图片描述

输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

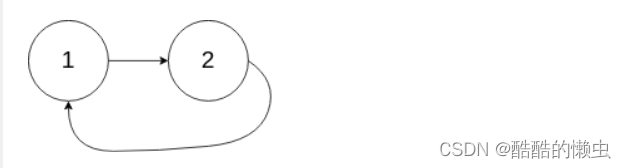
在这里插入图片描述

输入：head = [1,2], pos = 0
输出：返回索引为 0 的链表节点
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

在这里插入图片描述

输入：head = [1], pos = -1
输出：返回 null
解释：链表中没有环。

提示：

链表中节点的数目范围在范围 $0, 10^4]$ 内
$10^5 <= Node.val <= 10^5$
pos 的值为 -1 或者链表中的一个有效索引

进阶：你是否可以使用 $O (1)$ 空间解决此题？

💡思路：快慢指针

我们使用两个指针，slow 与 fast，它们起始分别指向链表的头部head 和头部的下一个节点head.next：

随后，slow 指针每次向后移动一个位置，而 fast 指针向后移动两个位置。
如果链表中存在环，则 fast 指针最终将再次与 slow 指针在环中相遇。

如下图所示，设链表中环外部分的长度为 a。slow 指针进入环后，又走了 b 的距离与 fast 相遇。此时，fast 指针已经走完了环的 n 圈，因此它走过的总距离为: $a + n (b + c) + b$

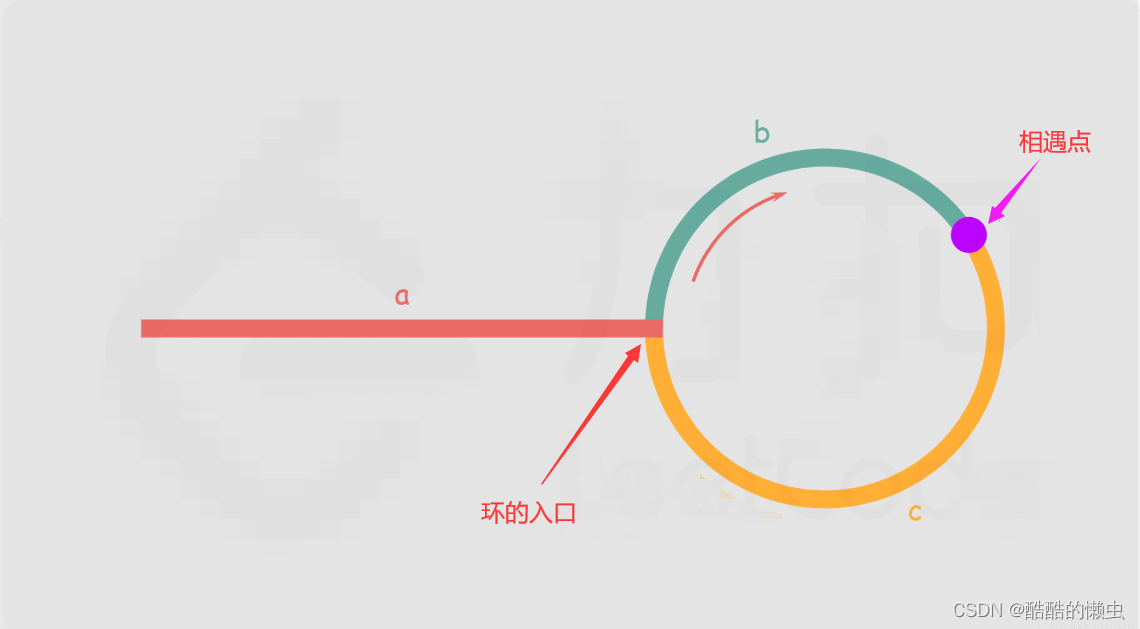
在这里插入图片描述
根据题意，任意时刻，fast指针走过的距离都为 slow 指针的 2 倍。因此，我们有
$a + (n + 1) b + n c = 2 (a + b)$
整理得：
$a = c + (n - 1) (b + c)$
我们会发现：从相遇点到入环点的距离加上 n−1 圈的环长，恰好等于从链表头部到入环点的距离。

因此，当发现 slow 与 fast 相遇后，我们让 fast 指向链表头部 head，slow 指向slow 的下一个：

随后， fast 和 slow 每次向后移动一个位置；
最终，它们会在 入环点 相遇。

🍁代码：(Java、C++)

Java

/*** Definition for singly-linked list.* class ListNode {*     int val;*     ListNode next;*     ListNode(int x) {*         val = x;*         next = null;*     }* }*/
public class Solution {public ListNode detectCycle(ListNode head) {if(head == null) return null;ListNode slow = head;ListNode fast = head.next;while(fast != null && fast.next != null){if(slow == fast) break;slow = slow.next;fast = fast.next.next;}if(fast == null || fast.next == null) return null;fast = head;slow = slow.next;while(slow != fast){slow = slow.next;fast = fast.next;}return slow;}
}

C++

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode(int x) : val(x), next(NULL) {}* };*/
class Solution {
public:ListNode *detectCycle(ListNode *head) {if(head == NULL) return NULL;ListNode* slow = head;ListNode* fast = head->next;while(fast != NULL && fast->next != NULL){if(slow == fast) break;slow = slow->next;fast = fast->next->next;}if(fast == NULL || fast->next == NULL) return NULL;fast = head;slow = slow->next;while(slow != fast){slow = slow->next;fast = fast->next;}return slow;}
};

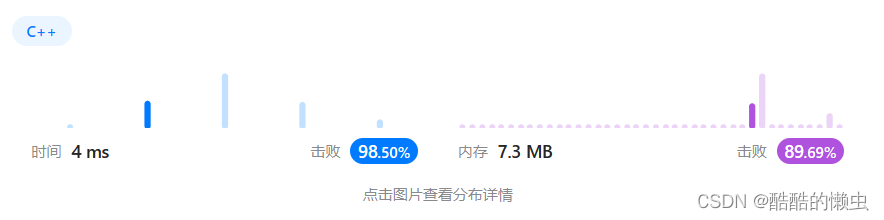
🚀 运行结果：

在这里插入图片描述

🕔 复杂度分析：

时间复杂度： $O (n)$ ，其中 n 为链表中节点的数目。在最初判断快慢指针是否相遇时，slow 指针走过的距离不会超过链表的总长度；随后寻找入环点时，走过的距离也不会超过链表的总长度。因此，总的执行时间为 $O (N) + O (N) = O (N)$ 。
空间复杂度： $O (1)$ ，我们只使用了 slow, fast 两个指针。