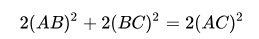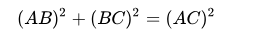三角形法则,有时候又叫三角形定则,在物理学中,用来表示两个力的合成(在数学中,是两个首尾相接的向量).

假如我们有两个方向的力,分别为a,b,当他们孤立的存在的时候,只是代表某个方向,以及在这个方向的力的大小,但是现实生活中,不可能只有单一方向的力,几乎所有物体的运动都受到不止一个力的作用,比如常见的重力,引力等等..

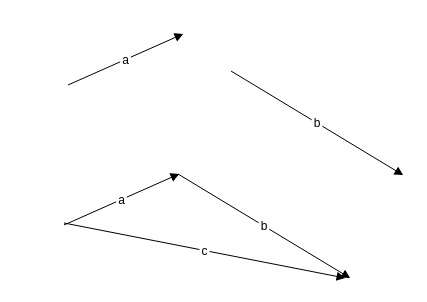
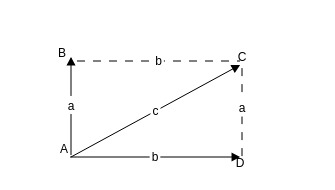
当力a(既有大小,又有方向的矢量,数学中叫向量,本质是一样的,表现形式不同而已)和力b首尾相接的时候,这两个力产生的作用力大小和方向是什么样的呢?答案就是c,就是把a的起点和b和终点连接起来,得到c,就是这两个力的合力,这就是物理世界中的规律.

得出:a+b=c

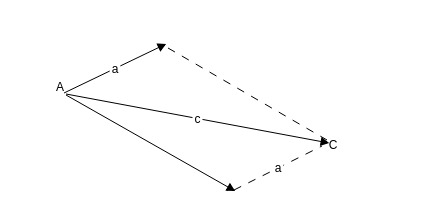
当a和b这两个力不是首尾相连,而是从同一个A点发出时,合成的力大小和方向又是哪个方向和大小呢?

由|a|(矢量的模长)和|b|组成的平行四边形的对角线就是他们的合力,起点在A,结束点在B,大小是对角线的长度.

也即是说,平行四边性的对角线就是合力的大小和方向.

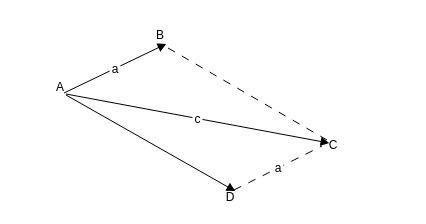
下面要说的是平行四边形的恒等式,先看下面的图:

当遇到特殊情形时(长方形):

就会变成我们熟悉的勾股定理:

至于证明方法,大家可以参考下,还是利用勾股定理来证明,将等式左右两边的公式进行替换,最后得到相同的表达式(通常等式证明也是这个思路,将被证明的等式两边都替换成相同的表达式)

平行四边形法则证明