一、前言
上篇文章讲解的是线性SVM的推导过程以及简化版SMO算法的代码实现。本篇文章将讲解SMO算法的优化方法以及非线性SVM。
本文出现的所有代码,均可在我的github上下载,欢迎Follow、Star:点击查看
二、SMO算法优化
在几百个点组成的小规模数据集上,简化版SMO算法的运行是没有什么问题的,但是在更大的数据集上的运行速度就会变慢。简化版SMO算法的第二个α的选择是随机的,针对这一问题,我们可以使用启发式选择第二个α值,来达到优化效果。
1、启发选择方式
下面这两个公式想必已经不再陌生:
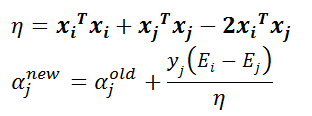
在实现SMO算法的时候,先计算η,再更新αj。为了加快第二个αj乘子的迭代速度,需要让直线的斜率增大,对于αj的更新公式,其中η值没有什么文章可做,于是只能令:

因此,我们可以明确自己的优化方法了:
- 最外层循环,首先在样本中选择违反KKT条件的一个乘子作为最外层循环,然后用"启发式选择"选择另外一个乘子并进行这两个乘子的优化
- 在非边界乘子中寻找使得 |Ei - Ej| 最大的样本
- 如果没有找到,则从整个样本中随机选择一个样本
接下来,让我们看看完整版SMO算法如何实现。
2、完整版SMO算法
完整版Platt SMO算法是通过一个外循环来选择违反KKT条件的一个乘子,并且其选择过程会在这两种方式之间进行交替:
- 在所有数据集上进行单遍扫描
- 在非边界α中实现单遍扫描
非边界α指的就是那些不等于边界0或C的α值,并且跳过那些已知的不会改变的α值。所以我们要先建立这些α的列表,用于才能出α的更新状态。
在选择第一个α值后,算法会通过"启发选择方式"选择第二个α值。
3、编写代码
我们首先构建一个仅包含init方法的optStruct类,将其作为一个数据结构来使用,方便我们对于重要数据的维护。代码思路和之前的简化版SMO算法是相似的,不同之处在于增加了优化方法,如果上篇文章已经看懂,我想这个代码会很好理解。创建一个svm-smo.py文件,编写代码如下:
# -*-coding:utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
import randomclass optStruct:"""数据结构,维护所有需要操作的值Parameters:dataMatIn - 数据矩阵classLabels - 数据标签C - 松弛变量toler - 容错率"""def __init__(self, dataMatIn, classLabels, C, toler):self.X = dataMatIn # 数据矩阵self.labelMat = classLabels # 数据标签self.C = C # 松弛变量self.tol = toler # 容错率self.m = np.shape(dataMatIn)[0] # 数据矩阵行数self.alphas = np.mat(np.zeros((self.m, 1))) # 根据矩阵行数初始化alpha参数为0self.b = 0 # 初始化b参数为0self.eCache = np.mat(np.zeros((self.m, 2))) # 根据矩阵行数初始化虎误差缓存,第一列为是否有效的标志位,第二列为实际的误差E的值。def loadDataSet(fileName):"""读取数据Parameters:fileName - 文件名Returns:dataMat - 数据矩阵labelMat - 数据标签"""dataMat = [];labelMat = []fr = open(fileName)for line in fr.readlines(): # 逐行读取,滤除空格等lineArr = line.strip().split('\t')dataMat.append([float(lineArr[0]), float(lineArr[1])]) # 添加数据labelMat.append(float(lineArr[2])) # 添加标签return dataMat, labelMatdef calcEk(oS, k):"""计算误差Parameters:oS - 数据结构k - 标号为k的数据Returns:Ek - 标号为k的数据误差"""fXk = float(np.multiply(oS.alphas, oS.labelMat).T * (oS.X * oS.X[k, :].T) + oS.b)Ek = fXk - float(oS.labelMat[k])return Ekdef selectJrand(i, m):"""函数说明:随机选择alpha_j的索引值Parameters:i - alpha_i的索引值m - alpha参数个数Returns:j - alpha_j的索引值"""j = i # 选择一个不等于i的jwhile (j == i):j = int(random.uniform(0, m))return jdef selectJ(i, oS, Ei):"""内循环启发方式2Parameters:i - 标号为i的数据的索引值oS - 数据结构Ei - 标号为i的数据误差Returns:j, maxK - 标号为j或maxK的数据的索引值Ej - 标号为j的数据误差"""maxK = -1;maxDeltaE = 0;Ej = 0 # 初始化oS.eCache[i] = [1, Ei] # 根据Ei更新误差缓存validEcacheList = np.nonzero(oS.eCache[:, 0].A)[0] # 返回误差不为0的数据的索引值if (len(validEcacheList)) > 1: # 有不为0的误差for k in validEcacheList: # 遍历,找到最大的Ekif k == i: continue # 不计算i,浪费时间Ek = calcEk(oS, k) # 计算EkdeltaE = abs(Ei - Ek) # 计算|Ei-Ek|if (deltaE > maxDeltaE): # 找到maxDeltaEmaxK = k;maxDeltaE = deltaE;Ej = Ekreturn maxK, Ej # 返回maxK,Ejelse: # 没有不为0的误差j = selectJrand(i, oS.m) # 随机选择alpha_j的索引值Ej = calcEk(oS, j) # 计算Ejreturn j, Ej # j,Ejdef updateEk(oS, k):"""计算Ek,并更新误差缓存Parameters:oS - 数据结构k - 标号为k的数据的索引值Returns:无"""Ek = calcEk(oS, k) # 计算EkoS.eCache[k] = [1, Ek] # 更新误差缓存def clipAlpha(aj, H, L):"""修剪alpha_jParameters:aj - alpha_j的值H - alpha上限L - alpha下限Returns:aj - 修剪后的alpah_j的值"""if aj > H:aj = Hif L > aj:aj = Lreturn ajdef innerL(i, oS):"""优化的SMO算法Parameters:i - 标号为i的数据的索引值oS - 数据结构Returns:1 - 有任意一对alpha值发生变化0 - 没有任意一对alpha值发生变化或变化太小"""# 步骤1:计算误差EiEi = calcEk(oS, i)# 优化alpha,设定一定的容错率。if ((oS.labelMat[i] * Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i] * Ei > oS.tol) and (oS.alphas[i] > 0)):# 使用内循环启发方式2选择alpha_j,并计算Ejj, Ej = selectJ(i, oS, Ei)# 保存更新前的aplpha值,使用深拷贝alphaIold = oS.alphas[i].copy();alphaJold = oS.alphas[j].copy();# 步骤2:计算上下界L和Hif (oS.labelMat[i] != oS.labelMat[j]):L = max(0, oS.alphas[j] - oS.alphas[i])H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])else:L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)H = min(oS.C, oS.alphas[j] + oS.alphas[i])if L == H:print("L==H")return 0# 步骤3:计算etaeta = 2.0 * oS.X[i, :] * oS.X[j, :].T - oS.X[i, :] * oS.X[i, :].T - oS.X[j, :] * oS.X[j, :].Tif eta >= 0:print("eta>=0")return 0# 步骤4:更新alpha_joS.alphas[j] -= oS.labelMat[j] * (Ei - Ej) / eta# 步骤5:修剪alpha_joS.alphas[j] = clipAlpha(oS.alphas[j], H, L)# 更新Ej至误差缓存updateEk(oS, j)if (abs(oS.alphas[j] - alphaJold) < 0.00001):print("alpha_j变化太小")return 0# 步骤6:更新alpha_ioS.alphas[i] += oS.labelMat[j] * oS.labelMat[i] * (alphaJold - oS.alphas[j])# 更新Ei至误差缓存updateEk(oS, i)# 步骤7:更新b_1和b_2b1 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.X[i, :] * oS.X[i, :].T - oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.X[i, :] * oS.X[j, :].Tb2 = oS.b - Ej - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.X[i, :] * oS.X[j, :].T - oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.X[j, :] * oS.X[j, :].T# 步骤8:根据b_1和b_2更新bif (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]):oS.b = b1elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]):oS.b = b2else:oS.b = (b1 + b2) / 2.0return 1else:return 0def smoP(dataMatIn, classLabels, C, toler, maxIter):"""完整的线性SMO算法Parameters:dataMatIn - 数据矩阵classLabels - 数据标签C - 松弛变量toler - 容错率maxIter - 最大迭代次数Returns:oS.b - SMO算法计算的boS.alphas - SMO算法计算的alphas"""oS = optStruct(np.mat(dataMatIn), np.mat(classLabels).transpose(), C, toler) # 初始化数据结构iter = 0 # 初始化当前迭代次数entireSet = True;alphaPairsChanged = 0while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)): # 遍历整个数据集都alpha也没有更新或者超过最大迭代次数,则退出循环alphaPairsChanged = 0if entireSet: # 遍历整个数据集for i in range(oS.m):alphaPairsChanged += innerL(i, oS) # 使用优化的SMO算法print("全样本遍历:第%d次迭代 样本:%d, alpha优化次数:%d" % (iter, i, alphaPairsChanged))iter += 1else: # 遍历非边界值nonBoundIs = np.nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0] # 遍历不在边界0和C的alphafor i in nonBoundIs:alphaPairsChanged += innerL(i, oS)print("非边界遍历:第%d次迭代 样本:%d, alpha优化次数:%d" % (iter, i, alphaPairsChanged))iter += 1if entireSet: # 遍历一次后改为非边界遍历entireSet = Falseelif (alphaPairsChanged == 0): # 如果alpha没有更新,计算全样本遍历entireSet = Trueprint("迭代次数: %d" % iter)return oS.b, oS.alphas # 返回SMO算法计算的b和alphasdef showClassifer(dataMat, classLabels, w, b):"""分类结果可视化Parameters:dataMat - 数据矩阵w - 直线法向量b - 直线解决Returns:无"""# 绘制样本点data_plus = [] # 正样本data_minus = [] # 负样本for i in range(len(dataMat)):if classLabels[i] > 0:data_plus.append(dataMat[i])else:data_minus.append(dataMat[i])data_plus_np = np.array(data_plus) # 转换为numpy矩阵data_minus_np = np.array(data_minus) # 转换为numpy矩阵plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1], s=30, alpha=0.7) # 正样本散点图plt.scatter(np.transpose(data_minus_np)[0], np.transpose(data_minus_np)[1], s=30, alpha=0.7) # 负样本散点图# 绘制直线x1 = max(dataMat)[0]x2 = min(dataMat)[0]a1, a2 = wb = float(b)a1 = float(a1[0])a2 = float(a2[0])y1, y2 = (-b - a1 * x1) / a2, (-b - a1 * x2) / a2plt.plot([x1, x2], [y1, y2])# 找出支持向量点for i, alpha in enumerate(alphas):if abs(alpha) > 0:x, y = dataMat[i]plt.scatter([x], [y], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolor='red')plt.show()def calcWs(alphas, dataArr, classLabels):"""计算wParameters:dataArr - 数据矩阵classLabels - 数据标签alphas - alphas值Returns:w - 计算得到的w"""X = np.mat(dataArr);labelMat = np.mat(classLabels).transpose()m, n = np.shape(X)w = np.zeros((n, 1))for i in range(m):w += np.multiply(alphas[i] * labelMat[i], X[i, :].T)return wif __name__ == '__main__':dataArr, classLabels = loadDataSet('testSet.txt')b, alphas = smoP(dataArr, classLabels, 0.6, 0.001, 40)w = calcWs(alphas, dataArr, classLabels)showClassifer(dataArr, classLabels, w, b)完整版SMO算法(上图)与简化版SMO算法(下图)运行结果对比如下图所示:
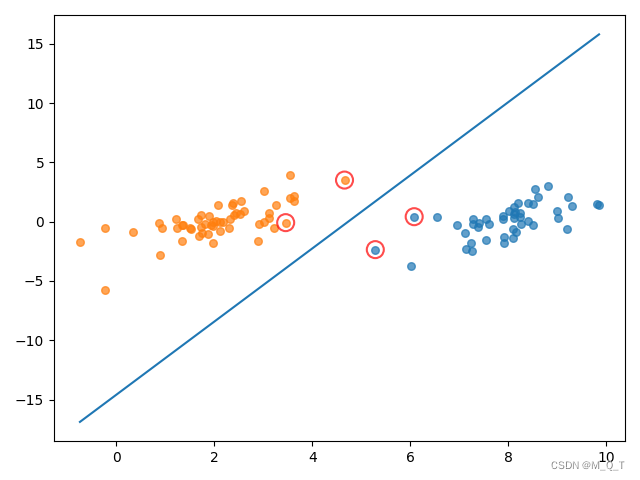

图中画红圈的样本点为支持向量上的点,是满足算法的一种解。完整版SMO算法覆盖整个数据集进行计算,而简化版SMO算法是随机选择的。可以看出,完整版SMO算法选出的支持向量样点更多,更接近理想的分隔超平面。
对比两种算法的运算时间,我的测试结果是完整版SMO算法的速度比简化版SMO算法的速度快6倍左右。
其实,优化方法不仅仅是简单的启发式选择,还有其他优化方法,SMO算法速度还可以进一步提高。但是鉴于文章进度,这里不再进行展开。感兴趣的朋友,可以移步这里进行理论学习:点我查看
三、非线性SVM
1、核技巧
我们已经了解到,SVM如何处理线性可分的情况,而对于非线性的情况,SVM的处理方式就是选择一个核函数。简而言之:在线性不可分的情况下,SVM通过某种事先选择的非线性映射(核函数)将输入变量映到一个高维特征空间,将其变成在高维空间线性可分,在这个高维空间中构造最优分类超平面。
根据上篇文章,线性可分的情况下,可知最终的超平面方程为:
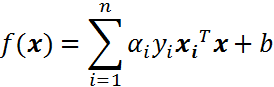
将上述公式用内积来表示:
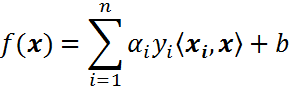
对于线性不可分,我们使用一个非线性映射,将数据映射到特征空间,在特征空间中使用线性学习器,分类函数变形如下:
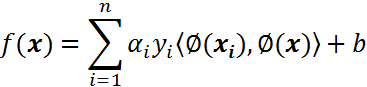
其中ϕ从输入空间(X)到某个特征空间(F)的映射,这意味着建立非线性学习器分为两步:
- 首先使用一个非线性映射将数据变换到一个特征空间F;
- 然后在特征空间使用线性学习器分类。
如果有一种方法可以在特征空间中直接计算内积 <ϕ(xi),ϕ(x)>,就像在原始输入点的函数中一样,就有可能将两个步骤融合到一起建立一个分线性的学习器,这样直接计算的方法称为核函数方法。
这里直接给出一个定义:核是一个函数k,对所有x,z∈X,满足k(x,z)=<ϕ(xi),ϕ(x)>,这里ϕ(·)是从原始输入空间X到内积空间F的映射。
简而言之:如果不是用核技术,就会先计算线性映ϕ(x1)和ϕ(x2),然后计算这它们的内积,使用了核技术之后,先把ϕ(x1)和ϕ(x2)的一般表达式<ϕ(x1),ϕ(x2)>=k(<ϕ(x1),ϕ(x2) >)计算出来,这里的<·,·>表示内积,k(·,·)就是对应的核函数,这个表达式往往非常简单,所以计算非常方便。
这种将内积替换成核函数的方式被称为核技巧(kernel trick)。
2、非线性数据处理
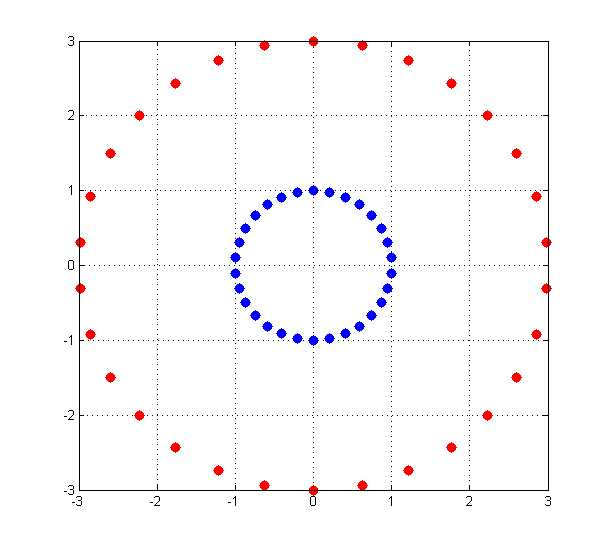
已经知道了核技巧是什么,但是为什么要这样做呢?我们先举一个简单的例子,进行说明。假设二维平面x-y上存在若干点,其中点集A服从 {x,y|x^2+y^2=1},点集B服从{x,y|x^2+y^2=9},那么这些点在二维平面上的分布是这样的:
正在上传…重新上传取消
蓝色的是点集A,红色的是点集B,他们在xy平面上并不能线性可分,即用一条直线分割( 虽然肉眼是可以识别的) 。采用映射(x,y)->(x,y,x^2+y^2)后,在三维空间的点的分布为:

可见红色和蓝色的点被映射到了不同的平面,在更高维空间中是线性可分的(用一个平面去分割)。
上述例子中的样本点的分布遵循圆的分布。继续推广到椭圆的一般样本形式:

可见红色和蓝色的点被映射到了不同的平面,在更高维空间中是线性可分的(用一个平面去分割)。
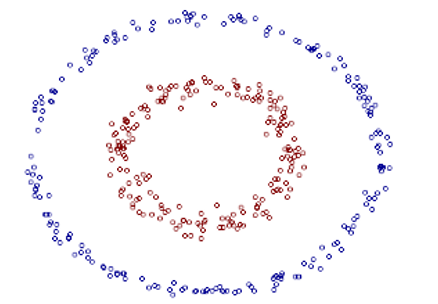
上述例子中的样本点的分布遵循圆的分布。继续推广到椭圆的一般样本形式:
正在上传…重新上传取消
上图的两类数据分布为两个椭圆的形状,这样的数据本身就是不可分的。不难发现,这两个半径不同的椭圆是加上了少量的噪音生成得到的。所以,一个理想的分界应该也是一个椭圆,而不是一个直线。如果用X1和X2来表示这个二维平面的两个坐标的话,我们知道这个分界椭圆可以写为:
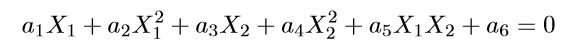
这个方程就是高中学过的椭圆一般方程。注意上面的形式,如果我们构造另外一个五维的空间,其中五个坐标的值分别为:
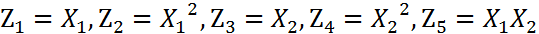
那么,显然我们可以将这个分界的椭圆方程写成如下形式:
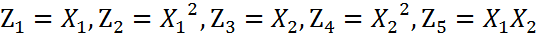
正在上传…重新上传取消
这个关于新的坐标Z1,Z2,Z3,Z4,Z5的方程,就是一个超平面方程,它的维度是5。也就是说,如果我们做一个映射 ϕ : 二维 → 五维,将 X1,X2按照上面的规则映射为 Z1,Z2,··· ,Z5,那么在新的空间中原来的数据将变成线性可分的,从而使用之前我们推导的线性分类算法就可以进行处理了。
我们举个简单的计算例子,现在假设已知的映射函数为:
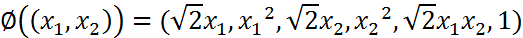
这个是一个从2维映射到5维的例子。如果没有使用核函数,根据上一小节的介绍,我们需要先结算映射后的结果,然后再进行内积运算。那么对于两个向量a1=(x1,x2)和a2=(y1,y2)有:
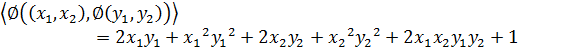
另外,如果我们不进行映射计算,直接运算下面的公式:
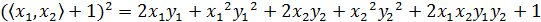
正在上传…重新上传取消
你会发现,这两个公式的计算结果是相同的。区别在于什么呢?
- 一个是根据映射函数,映射到高维空间中,然后再根据内积的公式进行计算,计算量大;
- 另一个则直接在原来的低维空间中进行计算,而不需要显式地写出映射后的结果,计算量小。
其实,在这个例子中,核函数就是:

我们通过k(x1,x2)的低维运算得到了先映射再内积的高维运算的结果,这就是核函数的神奇之处,它有效减少了我们的计算量。在这个例子中,我们对一个2维空间做映射,选择的新的空间是原始空间的所以一阶和二阶的组合,得到了5维的新空间;如果原始空间是3维的,那么我们会得到19维的新空间,这个数目是呈爆炸性增长的。如果我们使用ϕ(·)做映射计算,难度非常大,而且如果遇到无穷维的情况,就根本无从计算了。所以使用核函数进行计算是非常有必要的。
3、核技巧的实现
通过核技巧的转变,我们的分类函数变为:
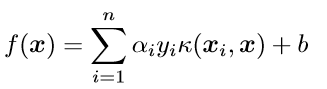
我们的对偶问题变成了:
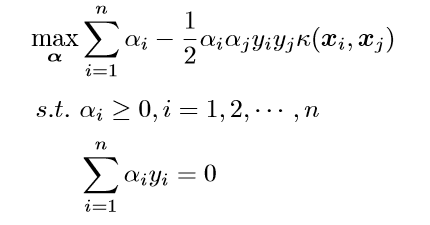
这样,我们就避开了高纬度空间中的计算。当然,我们刚刚的例子是非常简单的,我们可以手动构造出来对应映射的核函数出来,如果对于任意一个映射,要构造出对应的核函数就很困难了。因此,通常,人们会从一些常用的核函数中进行选择,根据问题和数据的不同,选择不同的参数,得到不同的核函数。接下来,要介绍的就是一个非常流行的核函数,那就是径向基核函数。
径向基核函数是SVM中常用的一个核函数。径向基核函数采用向量作为自变量的函数,能够基于向量举例运算输出一个标量。径向基核函数的高斯版本的公式如下:
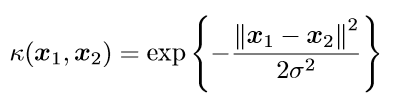
其中,σ是用户自定义的用于确定到达率(reach)或者说函数值跌落到0的速度参数。上述高斯核函数将数据从原始空间映射到无穷维空间。关于无穷维空间,我们不必太担心。高斯核函数只是一个常用的核函数,使用者并不需要确切地理解数据到底是如何表现的,而且使用高斯核函数还会得到一个理想的结果。如果σ选得很大的话,高次特征上的权重实际上衰减得非常快,所以实际上(数值上近似一下)相当于一个低维的子空间;反过来,如果σ选得很小,则可以将任意的数据映射为线性可分——当然,这并不一定是好事,因为随之而来的可能是非常严重的过拟合问题。不过,总的来说,通过调控参数σ,高斯核实际上具有相当高的灵活性,也是使用最广泛的核函数之一。
四、编程实现非线性SVM
接下来,我们将使用testSetRBF.txt和testSetRBF2.txt,前者作为训练集,后者作为测试集。数据集下载地址:点我查看
1、可视化数据集
我们先编写程序简单看下数据集:
import matplotlib.pyplot as plt
import numpy as npdef showDataSet(dataMat, labelMat):"""数据可视化Parameters:dataMat - 数据矩阵labelMat - 数据标签Returns:无"""data_plus = [] #正样本data_minus = [] #负样本for i in range(len(dataMat)):if labelMat[i] > 0:data_plus.append(dataMat[i])else:data_minus.append(dataMat[i])data_plus_np = np.array(data_plus) #转换为numpy矩阵data_minus_np = np.array(data_minus) #转换为numpy矩阵plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1]) #正样本散点图plt.scatter(np.transpose(data_minus_np)[0], np.transpose(data_minus_np)[1]) #负样本散点图plt.show()if __name__ == '__main__':dataArr,labelArr = loadDataSet('testSetRBF.txt') #加载训练集showDataSet(dataArr, labelArr)运行结果如下:
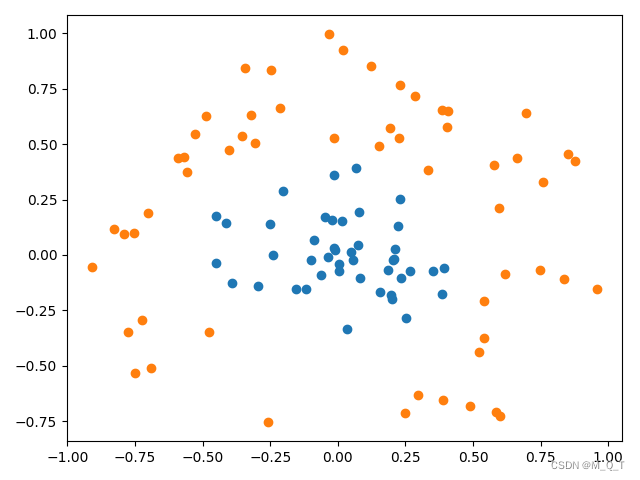
可见,数据明显是线性不可分的。下面我们根据公式,编写核函数,并增加初始化参数kTup用于存储核函数有关的信息,同时我们只要将之前的内积运算变成核函数的运算即可。最后编写testRbf()函数,用于测试。创建svmMLiA.py文件,编写代码如下:
# -*-coding:utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
import randomclass optStruct:"""数据结构,维护所有需要操作的值Parameters:dataMatIn - 数据矩阵classLabels - 数据标签C - 松弛变量toler - 容错率kTup - 包含核函数信息的元组,第一个参数存放核函数类别,第二个参数存放必要的核函数需要用到的参数"""def __init__(self, dataMatIn, classLabels, C, toler, kTup):self.X = dataMatIn #数据矩阵self.labelMat = classLabels #数据标签self.C = C #松弛变量self.tol = toler #容错率self.m = np.shape(dataMatIn)[0] #数据矩阵行数self.alphas = np.mat(np.zeros((self.m,1))) #根据矩阵行数初始化alpha参数为0 self.b = 0 #初始化b参数为0self.eCache = np.mat(np.zeros((self.m,2))) #根据矩阵行数初始化虎误差缓存,第一列为是否有效的标志位,第二列为实际的误差E的值。self.K = np.mat(np.zeros((self.m,self.m))) #初始化核Kfor i in range(self.m): #计算所有数据的核Kself.K[:,i] = kernelTrans(self.X, self.X[i,:], kTup)def kernelTrans(X, A, kTup): """通过核函数将数据转换更高维的空间Parameters:X - 数据矩阵A - 单个数据的向量kTup - 包含核函数信息的元组Returns:K - 计算的核K"""m,n = np.shape(X)K = np.mat(np.zeros((m,1)))if kTup[0] == 'lin': K = X * A.T #线性核函数,只进行内积。elif kTup[0] == 'rbf': #高斯核函数,根据高斯核函数公式进行计算for j in range(m):deltaRow = X[j,:] - AK[j] = deltaRow*deltaRow.TK = np.exp(K/(-1*kTup[1]**2)) #计算高斯核Kelse: raise NameError('核函数无法识别')return K #返回计算的核Kdef loadDataSet(fileName):"""读取数据Parameters:fileName - 文件名Returns:dataMat - 数据矩阵labelMat - 数据标签"""dataMat = []; labelMat = []fr = open(fileName)for line in fr.readlines(): #逐行读取,滤除空格等lineArr = line.strip().split('\t')dataMat.append([float(lineArr[0]), float(lineArr[1])]) #添加数据labelMat.append(float(lineArr[2])) #添加标签return dataMat,labelMatdef calcEk(oS, k):"""计算误差Parameters:oS - 数据结构k - 标号为k的数据Returns:Ek - 标号为k的数据误差"""fXk = float(np.multiply(oS.alphas,oS.labelMat).T*oS.K[:,k] + oS.b)Ek = fXk - float(oS.labelMat[k])return Ekdef selectJrand(i, m):"""函数说明:随机选择alpha_j的索引值Parameters:i - alpha_i的索引值m - alpha参数个数Returns:j - alpha_j的索引值"""j = i #选择一个不等于i的jwhile (j == i):j = int(random.uniform(0, m))return jdef selectJ(i, oS, Ei):"""内循环启发方式2Parameters:i - 标号为i的数据的索引值oS - 数据结构Ei - 标号为i的数据误差Returns:j, maxK - 标号为j或maxK的数据的索引值Ej - 标号为j的数据误差"""maxK = -1; maxDeltaE = 0; Ej = 0 #初始化oS.eCache[i] = [1,Ei] #根据Ei更新误差缓存validEcacheList = np.nonzero(oS.eCache[:,0].A)[0] #返回误差不为0的数据的索引值if (len(validEcacheList)) > 1: #有不为0的误差for k in validEcacheList: #遍历,找到最大的Ekif k == i: continue #不计算i,浪费时间Ek = calcEk(oS, k) #计算EkdeltaE = abs(Ei - Ek) #计算|Ei-Ek|if (deltaE > maxDeltaE): #找到maxDeltaEmaxK = k; maxDeltaE = deltaE; Ej = Ekreturn maxK, Ej #返回maxK,Ejelse: #没有不为0的误差j = selectJrand(i, oS.m) #随机选择alpha_j的索引值Ej = calcEk(oS, j) #计算Ejreturn j, Ej #j,Ejdef updateEk(oS, k):"""计算Ek,并更新误差缓存Parameters:oS - 数据结构k - 标号为k的数据的索引值Returns:无"""Ek = calcEk(oS, k) #计算EkoS.eCache[k] = [1,Ek] #更新误差缓存def clipAlpha(aj,H,L):"""修剪alpha_jParameters:aj - alpha_j的值H - alpha上限L - alpha下限Returns:aj - 修剪后的alpah_j的值"""if aj > H: aj = Hif L > aj:aj = Lreturn ajdef innerL(i, oS):"""优化的SMO算法Parameters:i - 标号为i的数据的索引值oS - 数据结构Returns:1 - 有任意一对alpha值发生变化0 - 没有任意一对alpha值发生变化或变化太小"""#步骤1:计算误差EiEi = calcEk(oS, i)#优化alpha,设定一定的容错率。if ((oS.labelMat[i] * Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i] * Ei > oS.tol) and (oS.alphas[i] > 0)):#使用内循环启发方式2选择alpha_j,并计算Ejj,Ej = selectJ(i, oS, Ei)#保存更新前的aplpha值,使用深拷贝alphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy();#步骤2:计算上下界L和Hif (oS.labelMat[i] != oS.labelMat[j]):L = max(0, oS.alphas[j] - oS.alphas[i])H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])else:L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)H = min(oS.C, oS.alphas[j] + oS.alphas[i])if L == H: print("L==H")return 0#步骤3:计算etaeta = 2.0 * oS.K[i,j] - oS.K[i,i] - oS.K[j,j]if eta >= 0: print("eta>=0")return 0#步骤4:更新alpha_joS.alphas[j] -= oS.labelMat[j] * (Ei - Ej)/eta#步骤5:修剪alpha_joS.alphas[j] = clipAlpha(oS.alphas[j],H,L)#更新Ej至误差缓存updateEk(oS, j)if (abs(oS.alphas[j] - alphaJold) < 0.00001): print("alpha_j变化太小")return 0#步骤6:更新alpha_ioS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])#更新Ei至误差缓存updateEk(oS, i)#步骤7:更新b_1和b_2b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,i] - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[i,j]b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,j]- oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[j,j]#步骤8:根据b_1和b_2更新bif (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): oS.b = b1elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): oS.b = b2else: oS.b = (b1 + b2)/2.0return 1else: return 0def smoP(dataMatIn, classLabels, C, toler, maxIter, kTup = ('lin',0)):"""完整的线性SMO算法Parameters:dataMatIn - 数据矩阵classLabels - 数据标签C - 松弛变量toler - 容错率maxIter - 最大迭代次数kTup - 包含核函数信息的元组Returns:oS.b - SMO算法计算的boS.alphas - SMO算法计算的alphas"""oS = optStruct(np.mat(dataMatIn), np.mat(classLabels).transpose(), C, toler, kTup) #初始化数据结构iter = 0 #初始化当前迭代次数entireSet = True; alphaPairsChanged = 0while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)): #遍历整个数据集都alpha也没有更新或者超过最大迭代次数,则退出循环alphaPairsChanged = 0if entireSet: #遍历整个数据集 for i in range(oS.m): alphaPairsChanged += innerL(i,oS) #使用优化的SMO算法print("全样本遍历:第%d次迭代 样本:%d, alpha优化次数:%d" % (iter,i,alphaPairsChanged))iter += 1else: #遍历非边界值nonBoundIs = np.nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0] #遍历不在边界0和C的alphafor i in nonBoundIs:alphaPairsChanged += innerL(i,oS)print("非边界遍历:第%d次迭代 样本:%d, alpha优化次数:%d" % (iter,i,alphaPairsChanged))iter += 1if entireSet: #遍历一次后改为非边界遍历entireSet = Falseelif (alphaPairsChanged == 0): #如果alpha没有更新,计算全样本遍历 entireSet = True print("迭代次数: %d" % iter)return oS.b,oS.alphas #返回SMO算法计算的b和alphasdef testRbf(k1 = 1.3):"""测试函数Parameters:k1 - 使用高斯核函数的时候表示到达率Returns:无"""dataArr,labelArr = loadDataSet('testSetRBF.txt') #加载训练集b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 100, ('rbf', k1)) #根据训练集计算b和alphasdatMat = np.mat(dataArr); labelMat = np.mat(labelArr).transpose()svInd = np.nonzero(alphas.A > 0)[0] #获得支持向量sVs = datMat[svInd] labelSV = labelMat[svInd];print("支持向量个数:%d" % np.shape(sVs)[0])m,n = np.shape(datMat)errorCount = 0for i in range(m):kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1)) #计算各个点的核predict = kernelEval.T * np.multiply(labelSV,alphas[svInd]) + b #根据支持向量的点,计算超平面,返回预测结果if np.sign(predict) != np.sign(labelArr[i]): errorCount += 1 #返回数组中各元素的正负符号,用1和-1表示,并统计错误个数print("训练集错误率: %.2f%%" % ((float(errorCount)/m)*100)) #打印错误率dataArr,labelArr = loadDataSet('testSetRBF2.txt') #加载测试集errorCount = 0datMat = np.mat(dataArr); labelMat = np.mat(labelArr).transpose() m,n = np.shape(datMat)for i in range(m):kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1)) #计算各个点的核 predict=kernelEval.T * np.multiply(labelSV,alphas[svInd]) + b #根据支持向量的点,计算超平面,返回预测结果if np.sign(predict) != np.sign(labelArr[i]): errorCount += 1 #返回数组中各元素的正负符号,用1和-1表示,并统计错误个数print("测试集错误率: %.2f%%" % ((float(errorCount)/m)*100)) #打印错误率def showDataSet(dataMat, labelMat):"""数据可视化Parameters:dataMat - 数据矩阵labelMat - 数据标签Returns:无"""data_plus = [] #正样本data_minus = [] #负样本for i in range(len(dataMat)):if labelMat[i] > 0:data_plus.append(dataMat[i])else:data_minus.append(dataMat[i])data_plus_np = np.array(data_plus) #转换为numpy矩阵data_minus_np = np.array(data_minus) #转换为numpy矩阵plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1]) #正样本散点图plt.scatter(np.transpose(data_minus_np)[0], np.transpose(data_minus_np)[1]) #负样本散点图plt.show()if __name__ == '__main__':testRbf()运行结果如下图所示:

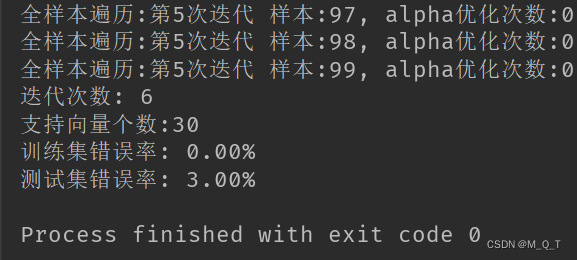
可以看到,训练集错误率为3%,测试集错误率都是4%。可以尝试更换不同的K1参数以观察测试错误率、训练错误率、支持向量个数随k1的变化情况。你会发现K1过大,会出现过拟合的情况,即训练集错误率低,但是测试集错误率高。
五、Sklearn构建SVM分类器
在第一篇文章中,我们使用了kNN进行手写数字识别。它的缺点是存储空间大,因为要保留所有的训练样本,如果你的老板让你节约这个内存空间,并达到相同的识别效果,甚至更好。那这个时候,我们就要可以使用SVM了,因为它只需要保留支持向量即可,而且能获得可比的效果。
使用的数据集还是kNN用到的数据集(testDigits和trainingDigits):点我查看
如果对这个数据集不了解的,可以先看看我的第一篇文章:
CSDN:点我查看
首先,我们先使用自己用python写的代码进行训练。创建文件svm-digits.py文件,编写代码如下:
# -*-coding:utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
import randomclass optStruct:"""数据结构,维护所有需要操作的值Parameters:dataMatIn - 数据矩阵classLabels - 数据标签C - 松弛变量toler - 容错率kTup - 包含核函数信息的元组,第一个参数存放核函数类别,第二个参数存放必要的核函数需要用到的参数"""def __init__(self, dataMatIn, classLabels, C, toler, kTup):self.X = dataMatIn #数据矩阵self.labelMat = classLabels #数据标签self.C = C #松弛变量self.tol = toler #容错率self.m = np.shape(dataMatIn)[0] #数据矩阵行数self.alphas = np.mat(np.zeros((self.m,1))) #根据矩阵行数初始化alpha参数为0 self.b = 0 #初始化b参数为0self.eCache = np.mat(np.zeros((self.m,2))) #根据矩阵行数初始化虎误差缓存,第一列为是否有效的标志位,第二列为实际的误差E的值。self.K = np.mat(np.zeros((self.m,self.m))) #初始化核Kfor i in range(self.m): #计算所有数据的核Kself.K[:,i] = kernelTrans(self.X, self.X[i,:], kTup)def kernelTrans(X, A, kTup): """通过核函数将数据转换更高维的空间Parameters:X - 数据矩阵A - 单个数据的向量kTup - 包含核函数信息的元组Returns:K - 计算的核K"""m,n = np.shape(X)K = np.mat(np.zeros((m,1)))if kTup[0] == 'lin': K = X * A.T #线性核函数,只进行内积。elif kTup[0] == 'rbf': #高斯核函数,根据高斯核函数公式进行计算for j in range(m):deltaRow = X[j,:] - AK[j] = deltaRow*deltaRow.TK = np.exp(K/(-1*kTup[1]**2)) #计算高斯核Kelse: raise NameError('核函数无法识别')return K #返回计算的核Kdef loadDataSet(fileName):"""读取数据Parameters:fileName - 文件名Returns:dataMat - 数据矩阵labelMat - 数据标签"""dataMat = []; labelMat = []fr = open(fileName)for line in fr.readlines(): #逐行读取,滤除空格等lineArr = line.strip().split('\t')dataMat.append([float(lineArr[0]), float(lineArr[1])]) #添加数据labelMat.append(float(lineArr[2])) #添加标签return dataMat,labelMatdef calcEk(oS, k):"""计算误差Parameters:oS - 数据结构k - 标号为k的数据Returns:Ek - 标号为k的数据误差"""fXk = float(np.multiply(oS.alphas,oS.labelMat).T*oS.K[:,k] + oS.b)Ek = fXk - float(oS.labelMat[k])return Ekdef selectJrand(i, m):"""函数说明:随机选择alpha_j的索引值Parameters:i - alpha_i的索引值m - alpha参数个数Returns:j - alpha_j的索引值"""j = i #选择一个不等于i的jwhile (j == i):j = int(random.uniform(0, m))return jdef selectJ(i, oS, Ei):"""内循环启发方式2Parameters:i - 标号为i的数据的索引值oS - 数据结构Ei - 标号为i的数据误差Returns:j, maxK - 标号为j或maxK的数据的索引值Ej - 标号为j的数据误差"""maxK = -1; maxDeltaE = 0; Ej = 0 #初始化oS.eCache[i] = [1,Ei] #根据Ei更新误差缓存validEcacheList = np.nonzero(oS.eCache[:,0].A)[0] #返回误差不为0的数据的索引值if (len(validEcacheList)) > 1: #有不为0的误差for k in validEcacheList: #遍历,找到最大的Ekif k == i: continue #不计算i,浪费时间Ek = calcEk(oS, k) #计算EkdeltaE = abs(Ei - Ek) #计算|Ei-Ek|if (deltaE > maxDeltaE): #找到maxDeltaEmaxK = k; maxDeltaE = deltaE; Ej = Ekreturn maxK, Ej #返回maxK,Ejelse: #没有不为0的误差j = selectJrand(i, oS.m) #随机选择alpha_j的索引值Ej = calcEk(oS, j) #计算Ejreturn j, Ej #j,Ejdef updateEk(oS, k):"""计算Ek,并更新误差缓存Parameters:oS - 数据结构k - 标号为k的数据的索引值Returns:无"""Ek = calcEk(oS, k) #计算EkoS.eCache[k] = [1,Ek] #更新误差缓存def clipAlpha(aj,H,L):"""修剪alpha_jParameters:aj - alpha_j的值H - alpha上限L - alpha下限Returns:aj - 修剪后的alpah_j的值"""if aj > H: aj = Hif L > aj:aj = Lreturn ajdef innerL(i, oS):"""优化的SMO算法Parameters:i - 标号为i的数据的索引值oS - 数据结构Returns:1 - 有任意一对alpha值发生变化0 - 没有任意一对alpha值发生变化或变化太小"""#步骤1:计算误差EiEi = calcEk(oS, i)#优化alpha,设定一定的容错率。if ((oS.labelMat[i] * Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i] * Ei > oS.tol) and (oS.alphas[i] > 0)):#使用内循环启发方式2选择alpha_j,并计算Ejj,Ej = selectJ(i, oS, Ei)#保存更新前的aplpha值,使用深拷贝alphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy();#步骤2:计算上下界L和Hif (oS.labelMat[i] != oS.labelMat[j]):L = max(0, oS.alphas[j] - oS.alphas[i])H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])else:L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)H = min(oS.C, oS.alphas[j] + oS.alphas[i])if L == H: print("L==H")return 0#步骤3:计算etaeta = 2.0 * oS.K[i,j] - oS.K[i,i] - oS.K[j,j]if eta >= 0: print("eta>=0")return 0#步骤4:更新alpha_joS.alphas[j] -= oS.labelMat[j] * (Ei - Ej)/eta#步骤5:修剪alpha_joS.alphas[j] = clipAlpha(oS.alphas[j],H,L)#更新Ej至误差缓存updateEk(oS, j)if (abs(oS.alphas[j] - alphaJold) < 0.00001): print("alpha_j变化太小")return 0#步骤6:更新alpha_ioS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])#更新Ei至误差缓存updateEk(oS, i)#步骤7:更新b_1和b_2b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,i] - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[i,j]b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,j]- oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[j,j]#步骤8:根据b_1和b_2更新bif (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): oS.b = b1elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): oS.b = b2else: oS.b = (b1 + b2)/2.0return 1else: return 0def smoP(dataMatIn, classLabels, C, toler, maxIter, kTup = ('lin',0)):"""完整的线性SMO算法Parameters:dataMatIn - 数据矩阵classLabels - 数据标签C - 松弛变量toler - 容错率maxIter - 最大迭代次数kTup - 包含核函数信息的元组Returns:oS.b - SMO算法计算的boS.alphas - SMO算法计算的alphas"""oS = optStruct(np.mat(dataMatIn), np.mat(classLabels).transpose(), C, toler, kTup) #初始化数据结构iter = 0 #初始化当前迭代次数entireSet = True; alphaPairsChanged = 0while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)): #遍历整个数据集都alpha也没有更新或者超过最大迭代次数,则退出循环alphaPairsChanged = 0if entireSet: #遍历整个数据集 for i in range(oS.m): alphaPairsChanged += innerL(i,oS) #使用优化的SMO算法print("全样本遍历:第%d次迭代 样本:%d, alpha优化次数:%d" % (iter,i,alphaPairsChanged))iter += 1else: #遍历非边界值nonBoundIs = np.nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0] #遍历不在边界0和C的alphafor i in nonBoundIs:alphaPairsChanged += innerL(i,oS)print("非边界遍历:第%d次迭代 样本:%d, alpha优化次数:%d" % (iter,i,alphaPairsChanged))iter += 1if entireSet: #遍历一次后改为非边界遍历entireSet = Falseelif (alphaPairsChanged == 0): #如果alpha没有更新,计算全样本遍历 entireSet = True print("迭代次数: %d" % iter)return oS.b,oS.alphas #返回SMO算法计算的b和alphasdef testRbf(k1 = 1.3):"""测试函数Parameters:k1 - 使用高斯核函数的时候表示到达率Returns:无"""dataArr,labelArr = loadDataSet('testSetRBF.txt') #加载训练集b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 100, ('rbf', k1)) #根据训练集计算b和alphasdatMat = np.mat(dataArr); labelMat = np.mat(labelArr).transpose()svInd = np.nonzero(alphas.A > 0)[0] #获得支持向量sVs = datMat[svInd] labelSV = labelMat[svInd];print("支持向量个数:%d" % np.shape(sVs)[0])m,n = np.shape(datMat)errorCount = 0for i in range(m):kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1)) #计算各个点的核predict = kernelEval.T * np.multiply(labelSV,alphas[svInd]) + b #根据支持向量的点,计算超平面,返回预测结果if np.sign(predict) != np.sign(labelArr[i]): errorCount += 1 #返回数组中各元素的正负符号,用1和-1表示,并统计错误个数print("训练集错误率: %.2f%%" % ((float(errorCount)/m)*100)) #打印错误率dataArr,labelArr = loadDataSet('testSetRBF2.txt') #加载测试集errorCount = 0datMat = np.mat(dataArr); labelMat = np.mat(labelArr).transpose() m,n = np.shape(datMat)for i in range(m):kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1)) #计算各个点的核 predict=kernelEval.T * np.multiply(labelSV,alphas[svInd]) + b #根据支持向量的点,计算超平面,返回预测结果if np.sign(predict) != np.sign(labelArr[i]): errorCount += 1 #返回数组中各元素的正负符号,用1和-1表示,并统计错误个数print("测试集错误率: %.2f%%" % ((float(errorCount)/m)*100)) #打印错误率def showDataSet(dataMat, labelMat):"""数据可视化Parameters:dataMat - 数据矩阵labelMat - 数据标签Returns:无"""data_plus = [] #正样本data_minus = [] #负样本for i in range(len(dataMat)):if labelMat[i] > 0:data_plus.append(dataMat[i])else:data_minus.append(dataMat[i])data_plus_np = np.array(data_plus) #转换为numpy矩阵data_minus_np = np.array(data_minus) #转换为numpy矩阵plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1]) #正样本散点图plt.scatter(np.transpose(data_minus_np)[0], np.transpose(data_minus_np)[1]) #负样本散点图plt.show()if __name__ == '__main__':testRbf()SMO算法实现部分跟上文是一样的,我们新创建了img2vector()、loadImages()、testDigits()函数,它们分别用于二进制图形转换、图片加载、训练SVM分类器。我们自己的SVM分类器是个二类分类器,所以在设置标签的时候,将9作为负类,其余的0-8作为正类,进行训练。这是一种'ovr'思想,即one vs rest,就是对一个类别和剩余所有的类别进行分类。如果想实现10个数字的识别,一个简单的方法是,训练出10个分类器。这里简单起见,只训练了一个用于分类9和其余所有数字的分类器,运行结果如下:
可以看到,虽然我们进行了所谓的"优化",但是训练仍然很耗时,迭代10次,花费了307.4s。因为我们没有多进程、没有设置自动的终止条件,总之一句话,需要优化的地方太多了。尽管如此,我们训练后得到的结果还是不错的,可以看到训练集错误率为0,测试集错误率也仅为0.01%。
接下来,就是讲解本文的重头戏:sklearn.svm.SVC。
1、sklearn.svm.SVC
官方英文文档手册:点我查看
sklearn.svm模块提供了很多模型供我们使用,本文使用的是svm.SVC,它是基于libsvm实现的。
让我们先看下SVC这个函数,一共有14个参数:

参数说明如下:
- C:惩罚项,float类型,可选参数,默认为1.0,C越大,即对分错样本的惩罚程度越大,因此在训练样本中准确率越高,但是泛化能力降低,也就是对测试数据的分类准确率降低。相反,减小C的话,容许训练样本中有一些误分类错误样本,泛化能力强。对于训练样本带有噪声的情况,一般采用后者,把训练样本集中错误分类的样本作为噪声。
- kernel:核函数类型,str类型,默认为'rbf'。可选参数为:
- 'linear':线性核函数
- 'poly':多项式核函数
- 'rbf':径像核函数/高斯核
- 'sigmod':sigmod核函数
- 'precomputed':核矩阵
- precomputed表示自己提前计算好核函数矩阵,这时候算法内部就不再用核函数去计算核矩阵,而是直接用你给的核矩阵,核矩阵需要为n*n的。
- degree:多项式核函数的阶数,int类型,可选参数,默认为3。这个参数只对多项式核函数有用,是指多项式核函数的阶数n,如果给的核函数参数是其他核函数,则会自动忽略该参数。
- gamma:核函数系数,float类型,可选参数,默认为auto。只对'rbf' ,'poly' ,'sigmod'有效。如果gamma为auto,代表其值为样本特征数的倒数,即1/n_features。
- coef0:核函数中的独立项,float类型,可选参数,默认为0.0。只有对'poly' 和,'sigmod'核函数有用,是指其中的参数c。
- probability:是否启用概率估计,bool类型,可选参数,默认为False,这必须在调用fit()之前启用,并且会fit()方法速度变慢。
- shrinking:是否采用启发式收缩方式,bool类型,可选参数,默认为True。
- tol:svm停止训练的误差精度,float类型,可选参数,默认为1e^-3。
- cache_size:内存大小,float类型,可选参数,默认为200。指定训练所需要的内存,以MB为单位,默认为200MB。
- class_weight:类别权重,dict类型或str类型,可选参数,默认为None。给每个类别分别设置不同的惩罚参数C,如果没有给,则会给所有类别都给C=1,即前面参数指出的参数C。如果给定参数'balance',则使用y的值自动调整与输入数据中的类频率成反比的权重。
- verbose:是否启用详细输出,bool类型,默认为False,此设置利用libsvm中的每个进程运行时设置,如果启用,可能无法在多线程上下文中正常工作。一般情况都设为False,不用管它。
- max_iter:最大迭代次数,int类型,默认为-1,表示不限制。
- decision_function_shape:决策函数类型,可选参数'ovo'和'ovr',默认为'ovr'。'ovo'表示one vs one,'ovr'表示one vs rest。
- random_state:数据洗牌时的种子值,int类型,可选参数,默认为None。伪随机数发生器的种子,在混洗数据时用于概率估计。
其实,只要自己写了SMO算法,每个参数的意思,大概都是能明白的。
2、编写代码
SVC很是强大,我们不用理解算法实现的具体细节,不用理解算法的优化方法。同时,它也满足我们的多分类需求。创建文件svm-svc.py文件,编写代码如下:
# -*- coding: UTF-8 -*-
import numpy as np
import operator
from os import listdir
from sklearn.svm import SVCdef img2vector(filename):"""将32x32的二进制图像转换为1x1024向量。Parameters:filename - 文件名Returns:returnVect - 返回的二进制图像的1x1024向量"""#创建1x1024零向量returnVect = np.zeros((1, 1024))#打开文件fr = open(filename)#按行读取for i in range(32):#读一行数据lineStr = fr.readline()#每一行的前32个元素依次添加到returnVect中for j in range(32):returnVect[0, 32*i+j] = int(lineStr[j])#返回转换后的1x1024向量return returnVectdef handwritingClassTest():"""手写数字分类测试Parameters:无Returns:无"""#测试集的LabelshwLabels = []#返回trainingDigits目录下的文件名trainingFileList = listdir('trainingDigits')#返回文件夹下文件的个数m = len(trainingFileList)#初始化训练的Mat矩阵,测试集trainingMat = np.zeros((m, 1024))#从文件名中解析出训练集的类别for i in range(m):#获得文件的名字fileNameStr = trainingFileList[i]#获得分类的数字classNumber = int(fileNameStr.split('_')[0])#将获得的类别添加到hwLabels中hwLabels.append(classNumber)#将每一个文件的1x1024数据存储到trainingMat矩阵中trainingMat[i,:] = img2vector('trainingDigits/%s' % (fileNameStr))clf = SVC(C=200,kernel='rbf')clf.fit(trainingMat,hwLabels)#返回testDigits目录下的文件列表testFileList = listdir('testDigits')#错误检测计数errorCount = 0.0#测试数据的数量mTest = len(testFileList)#从文件中解析出测试集的类别并进行分类测试for i in range(mTest):#获得文件的名字fileNameStr = testFileList[i]#获得分类的数字classNumber = int(fileNameStr.split('_')[0])#获得测试集的1x1024向量,用于训练vectorUnderTest = img2vector('testDigits/%s' % (fileNameStr))#获得预测结果# classifierResult = classify0(vectorUnderTest, trainingMat, hwLabels, 3)classifierResult = clf.predict(vectorUnderTest)print("分类返回结果为%d\t真实结果为%d" % (classifierResult, classNumber))if(classifierResult != classNumber):errorCount += 1.0print("总共错了%d个数据\n错误率为%f%%" % (errorCount, errorCount/mTest * 100))if __name__ == '__main__':handwritingClassTest()代码和kNN的实现是差不多的,就是换了个分类器而已。运行结果如下:
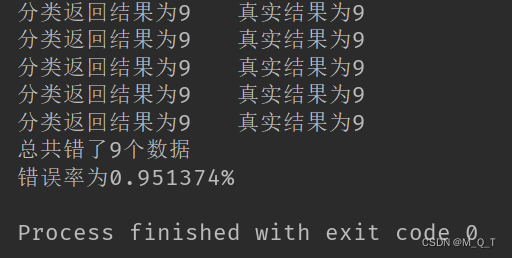
可以看到,训练和测试的时间总共加起来才7.3s。而且,测试集的错误率仅为1.37%。试着改变SVC的参数,慢慢体会一下吧~
六、总结
1、SVM的优缺点
优点
- 可用于线性/非线性分类,也可以用于回归,泛化错误率低,也就是说具有良好的学习能力,且学到的结果具有很好的推广性。
- 可以解决小样本情况下的机器学习问题,可以解决高维问题,可以避免神经网络结构选择和局部极小点问题。
- SVM是最好的现成的分类器,现成是指不加修改可直接使用。并且能够得到较低的错误率,SVM可以对训练集之外的数据点做很好的分类决策。
缺点
- 对参数调节和和函数的选择敏感。
参考:
[1]https://cuijiahua.com/blog/2017/11/ml_9_svm_2.html
[2]《机器学习实战》