halcon中有几个算子有点类似，看了下区别

1.vector_to_rigid( : : Px, Py, Qx, Qy : HomMat2D)

2.vector_to_similarity( : : Px, Py, Qx, Qy : HomMat2D)

3.vector_to_aniso( : : Px, Py, Qx, Qy : HomMat2D)

vector_to_rigid 这个是刚性变换，

 只有旋转和平移。

vector_to_similarity 这个是相似变换

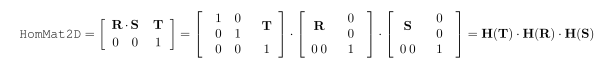
旋转和平移，加各方向等比例缩放

 vector_to_aniso 仿射变换

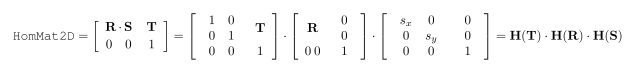
旋转、平移、各方向不同比例缩放

以上算子都可以到到对应的仿射矩阵。

思考原理，通过两组点怎么通过计算得到仿射矩阵

仿射矩阵形式为：

点A(x1,y1) 到点B(X1,Y1) 对用关系即为 X1=a1*x1+a2*y1+a3  Y1=a4*x1+a5*y1+a6

多个点就多个线性方程，最终是一个求解线性方程组的问题

转成矩阵形式即为(这里使用了3个点，可以更多）

在halcon中可以使用solve_matrix解矩阵

测试了两组数据，由点x变换到点y

x1:=[19,549]
x2:=[19,663]
x3:=[275,547]
x4:=[274,664]

y1:=[267,1134]
y2:=[331,1159]
y3:=[429,558]
y4:=[496,585]

用vector_to_aniso算子得到的变换矩阵为

[0.64363, 0.583832, -67.3593, -2.24947, 0.167049, 1087.92]

通过解矩阵方式得到的变换矩阵为

[0.64103, 0.569983, -58.5884, -2.25006, 0.215317, 1058.77]

基本一致，但为何不是相等，有点思路，但还没搞清楚

如图两个仿射变换如图

 halcon代码

read_image (Image, 'printer_chip/printer_chip_01')x1:=[19,549]
x2:=[19,663]
x3:=[275,547]
x4:=[274,664]gen_cross_contour_xld (Cross1, 19, 549, 6, 0.785398)
gen_cross_contour_xld (Cross2, 19, 663, 6, 0.785398)
gen_cross_contour_xld (Cross3, 275, 547, 6, 0.785398)
gen_cross_contour_xld (Cross4, 274, 664, 6, 0.785398)
gen_rectangle2 (ROI_0, 382.107, 860.444, rad(15.9103), 294.57, 32.8626)y1:=[267,1134]
y2:=[331,1159]
y3:=[429,558]
y4:=[496,585]X1:=[x1[0],x2[0],x3[0],x4[0]]
Y1:=[x1[1],x2[1],x3[1],x4[1]]X2:=[y1[0],y2[0],y3[0],y4[0]]
Y2:=[y1[1],y2[1],y3[1],y4[1]]gen_contour_polygon_xld (Contour, X2, Y2)
vector_to_aniso(X1, Y1, X2, Y2, HomMat2D)
affine_trans_image (Image, ImageAffineTrans, HomMat2D, 'constant', 'false')create_matrix(8,6,0,MatrixA)
Values:=[x1[0],x1[1],1,0,0,0,0,0,0,x1[0],x1[1],1,x2[0],x2[1],1,0,0,0,0,0,0,x2[0],x2[1],1,x3[0],x3[1],1,0,0,0,0,0,0,x3[0],x3[1],1,x4[0],x4[1],1,0,0,0,0,0,0,x4[0],x4[1],1]
set_full_matrix (MatrixA, Values)Values2:=[y1[0],y1[1],y2[0],y2[1],y3[0],y3[1],y4[0],y4[1]]
create_matrix(8,1,0,MatrixB)
set_full_matrix (MatrixB, Values2)solve_matrix (MatrixA, 'general', 0, MatrixB, MatrixResultID)get_value_matrix (MatrixResultID, 0, 0, Value1)
get_value_matrix (MatrixResultID, 1, 0, Value2)
get_value_matrix (MatrixResultID, 2, 0, Value3)
get_value_matrix (MatrixResultID, 3, 0, Value4)
get_value_matrix (MatrixResultID, 4, 0, Value5)
get_value_matrix (MatrixResultID, 5, 0, Value6)myHom2d:=[Value1,Value2,Value3,Value4,Value5,Value6,0,0,1]affine_trans_image (Image, ImageAffineTrans1, myHom2d, 'constant', 'false')boundary (ImageAffineTrans, RegionBorder, 'inner')
boundary (ImageAffineTrans1, RegionBorder1, 'inner')dev_display (Image)
dev_display (ImageAffineTrans)
dev_display (ImageAffineTrans1)dev_set_color ('red')
dev_display (RegionBorder)dev_set_color ('green')
dev_display (RegionBorder1)dev_display (Contour)