2010年风靡全球的“水果忍者”游戏,想必大家肯定都玩过吧?(没玩过也没关系啦~)在游戏当中,画面里会随机地弹射出一系列的水果与炸弹,玩家尽可能砍掉所有的水果而避免砍中炸弹,就可以完成游戏规定的任务。如果玩家可以一刀砍下画面当中一连串的水果,则会有额外的奖励,如图1所示。

图 1
现在假如你是“水果忍者”游戏的玩家,你要做的一件事情就是,将画面当中的水果一刀砍下。这个问题看上去有些复杂,让我们把问题简化一些。我们将游戏世界想象成一个二维的平面。游戏当中的每个水果被简化成一条一条的垂直于水平线的竖直线段。而一刀砍下我们也仅考虑成能否找到一条直线,使之可以穿过所有代表水果的线段。
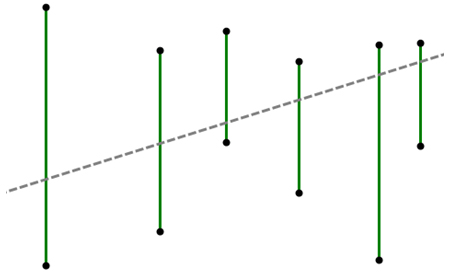
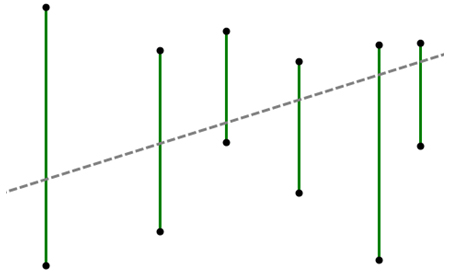
图 2
如图2所示,其中绿色的垂直线段表示的就是一个一个的水果;灰色的虚线即表示穿过所有线段的某一条直线。可以从上图当中看出,对于这样一组线段的排列,我们是可以找到一刀切开所有水果的方案的。
另外,我们约定,如果某条直线恰好穿过了线段的端点也表示它砍中了这个线段所表示的水果。假如你是这样一个功能的开发者,你要如何来找到一条穿过它们的直线呢?
输入格式:
输入在第一行给出一个正整数N(≤104),表示水果的个数。随后N行,每行给出三个整数x、y1、y2,其间以空格分隔,表示一条端点为(x,y1)和(x,y2)的水果,其中y1>y2。注意:给出的水果输入集合一定存在一条可以将其全部穿过的直线,不需考虑不存在的情况。坐标为区间 [−106,106) 内的整数。
输出格式:
在一行中输出穿过所有线段的直线上具有整数坐标的任意两点p1(x1,y1)和p2(x2,y2),格式为 x1y1x2y2。注意:本题答案不唯一,由特殊裁判程序判定,但一定存在四个坐标全是整数的解。
输入样例:
5
-30 -52 -84
38 22 -49
-99 -22 -99
48 59 -18
-36 -50 -72
输出样例:
-99 -99 -30 -52对于这道题目的思路。应该遍历每一个地址,应为根据题目说的,必然有一个点是,那么我就把他们全部遍历调取,如果恰好符合条件那么久直接进行输出,代码如下,先每次确定一个一个地址位置,这里将数据看作从左往右,一个位置也就是一个向下的线段,找到他做下面的顶点,然后我就要在其他所有的线段里面找到他们的上面的那个顶点,在这个上面的顶点和我们选中的最下面的这个顶点之间的斜率恰好穿过所有线段,思路是这样的,那么具体实现就要看遍历的时候,如果遍历的线段的斜率的最大值在我们设定的【maxi,mini】之间的话,那么就说明这个点可取,在对这个点进行分析他的斜率是由哪俩个点构成的,及时更新maxi和mini,并且对于我们结果的端点值进行锁定,这样的话如果我们完整的进行了一趟遍历,就可以直接输出了,应为我们如果不能完整遍历的话,就不符合输出条件。
#include<iostream>
using namespace std;
const long long INF=1e+9;
long long x[10010],up[10010],down[10010];
int main()
{long long sum;long long xi,y;cin>>sum;for(long long n=0;n<sum;n++)cin>>x[n]>>up[n]>>down[n];for(long long n=0;n<sum;n++){double maxi=INF;double mini=-INF;long long m;for(m=0;m<sum;m++){if(n!=m){double a=1.0*(up[m]-down[n])/(x[m]-x[n]);double b=1.0*(down[m]-down[n])/(x[m]-x[n]);bool flag=true;if(a<b){swap(a,b);flag=false;}if(mini>a)break;if(a<maxi){maxi=a;if(flag){xi=x[m];y=up[m];}else{xi=x[m];y=down[m];}}mini=max(mini,b);}}if(m==sum){cout<<x[n]<<" "<<down[n]<<" "<<xi<<" "<<y<<endl;break;}}return 0;
}