上一期：粒子群算法（1）

线性递减惯性权重

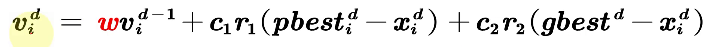
在这里插入图片描述
惯性权重w体现的是粒子继承先前的速度的能力，Shi,Y最先将惯性权重w引入到粒子群算法中，并分析指出一个较大的惯性权值有利于全局搜索，而一个较小的权值则更利于局部搜索。为了更好地平衡算法的全局搜索以及局部搜索能力，Shi,Y提出了线性递减惯性权重LDIW(Linear Decreasing Inertia Weight),公式如下:
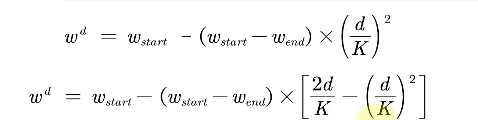
在这里插入图片描述

其他非线性递减

在这里插入图片描述

自适应惯性权重

在这里插入图片描述
一个较大的惯性权值有利于全局搜索而一个较小的权值则更利于局部搜索

随机惯性权重

最开始提出随机惯性权重的论文: Zhang L, Yu H , Hu S . A New Approach to lmproveParticle Swarm Optimization[J]. lecture notes in computer science, 2003,2723:134-139.

其他随机数

在这里插入图片描述

参考文献:基于随机惯性权重的简化粒子群优化算法[J].计算机应用研究,2014,031(002):361-363,391.

压缩因子法

在这里插入图片描述

参考文献: M.Clerc. The swarm and queen: towards a deterministic and adaptive particleswarm op-timization.Proc.Congress on Evolutionary Computation,Washington, DC…Piscataway,NJ:IEEE Service Center (1999)1951-1957

在这里插入图片描述

参考文献:
Eberhart R C. Comparing inertia weights andconstriction factors in optimization[c//Proceedings of the 2000 IEEE Congress on Evolutionary Computation, La Jolla,CA. IEEE,2000.

非对称学习因子

在这里插入图片描述

参考文献:毛开富,包广清,徐驰.基于非对称学习因子调节的粒子群优化算法[叮.计算机工程,2010(19):188-190.

测试函数

当你提出了一种新的优化算法后，你需要和别人之前提出的算法来进行PK,看你的算法有没有提高，下表给出了四种常见的测试函数:
在这里插入图片描述
维数:自变量x的个数,也是上面表达式中n的大小
取值范围:每个x对应的变化范围
理论极值:这个函数理论上的最小值
误差目标:只要我们求出来的最小值小于这个目标值就能被接受

张玮,王华奎.粒子群算法稳定性的参数选择策略分析[J.系统仿真学报，2009, 21(014):4339-4344.

改进

当粒子已经找到最佳位置后，再增加迭代次数只会浪费计算时间，那么我们能否设计一个策略，能够自动退出迭代呢?
(1）初始化最大迭代次数、计数器以及最大计数值（例如分别取100,0, 20)(2）定义“函数变化量容忍度”．一般取非常小的正数，例如10^(-6);
(3）在迭代的过程中，每次计算出来最佳适应度后,都计算该适应度和上一次迭代时最佳适应度的变化室(取绝对值);
(4)判断这个变化量和"函数变化量容忍度"的相对大小，如果前者小,则计数器加1;否则计数器清;
(5）不断重复这个过程,有以下两种可能:
①此时还没有超过最大迭代次数，计数器的值超过了最大计数值，那么我们
就跳出迭代循环，搜索结束。
②此时已经达到了最大迭代次数，那么直接跳出循环，搜索结束。

MATLAB自带函数

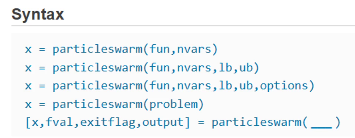
在这里插入图片描述

该函数主要参考的两篇文章:(该信息可在Matlab官网中查询)
[1]Mezura-Montes, E., and C.A.Coello Coello. “Constraint-handling in nature-inspired numerical optimization:Past, present and future.” Swarm and Evolutionary Computation.2011, pp. 173-194.
[2] Pedersen,M.E.“Good Parameters for Particle Swarm Optimization.” Luxembourg: Hvass Laboratories, 2010.

在这里插入图片描述