特别行动队
【问题描述】
你有一支由 n 名预备役士兵组成的部队,士兵从 1 到 n 编号,要将他们拆分成若干特别行动队调入战场。出于默契的考虑,同一支特别行动队中队员的编号应该连续,即为形如(i, i + 1, …, i + k)的序列。
编号为 i 的士兵的初始战斗力为 xi ,一支特别行动队的初始战斗力 x 为队内士兵初始战斗力之和,即 x = xi + xi+1 + … + xi+k。
通过长期的观察,你总结出一支特别行动队的初始战斗力 x 将按如下经验公式修正为 x':x' = ax2 + bx + c,其中 a, b, c 是已知的系数(a < 0)。
作为部队统帅,现在你要为这支部队进行编队,使得所有特别行动队修正后战斗力之和最大。试求出这个最大和。
例如,你有 4 名士兵,x1 = 2, x2 = 2, x3 = 3, x4 = 4。经验公式中的参数为 a = –1,b = 10, c = –20。此时,最佳方案是将士兵组成 3 个特别行动队:第一队包含士兵
1 和士兵 2,第二队包含士兵 3,第三队包含士兵 4。特别行动队的初始战斗力分别为 4, 3, 4,修正后的战斗力分别为 4, 1, 4。修正后的战斗力和为 9,没有其它
方案能使修正后的战斗力和更大。
【输入格式】
输入由三行组成。第一行包含一个整数 n,表示士兵的总数。第二行包含三个整数 a, b, c,经验公式中各项的系数。第三行包含 n 个用空格分隔的整数 x1,x2, …, xn,分别表示编号为 1, 2, …, n 的士兵的初始战斗力。
【输出格式】
输出一个整数,表示所有特别行动队修正后战斗力[斜率优化] 特别行动队 commando
news/2025/3/29 19:34:59/
相关文章
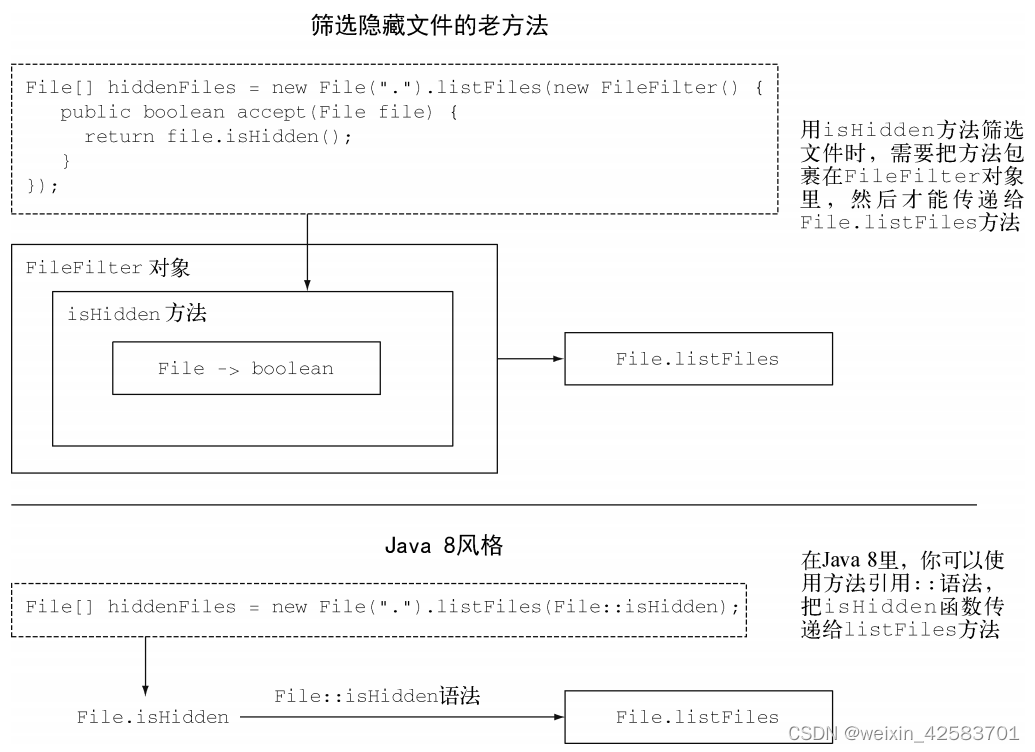
Java8实战-总结2
Java8实战-总结2 基础知识方法和Lambda传递代码:一个例子从传递方法到Lambda 基础知识
方法和Lambda
Scala和Groovy等语言的实践已经证明,让方法等概念作为一等值可以扩充程序员的工具库,从而让编程变得更容易。一旦程序员熟悉了这个强大的…
Command(命令)
Command(命令) 行为型 对象 1
Intent_意图2
将“请求”封装成对象,以使用不同的请求、队列或者日志来参数化其他对象。命令模式也支持可撤销的操作
Motivation_动机3
在系统中,行为请求者与行为实现者通常是一种紧耦合的关系&…
I - Commando War
先读懂题意,先排序,在相加,贪心算法重在思路。 I - Commando War Time Limit:1000MS Memory Limit:0KB 64bit IO Format:%lld & %llu Submit Status Description G Commando War Input: Standard Input Output: Standard …
commands(commands软件)
QQ任逍遥为什么老“badsequenceofcommands”? bad sequence of commands的意思是:命令的次序错误。 WINDOWS动态链接库中文件丢失会造成软件运行参数错误,就会造成你的这个现象。 所以很可能是你的软件运行时参数有问题,电脑提示bad seque…
Command命令模式
简介:
简单来说,就像我们的复制、删除、插入等等都是命令,我们将命令封装为一个对象,并且支持撤销,将一系列命令串成一条链或者与链表结合使用,可以实现一系列的do和undo
模式类图: command: …
more command
文章目录 1.命令简介2.命令格式3.选项说明4.交互式命令5.环境变量6.常用示例参考文献 1.命令简介
more 是常用的文本文件阅读工具。
more 类似于 cat,不过以一页一页的形式显示,便于逐页阅读。一般文件过大时使用 more 浏览,文件较小时使用…
commandos 系列
盟军敢死队1秘籍2008-03-23 12:42 无敌密技: 游戏进行中打GONZO1982或1982GONZO,然后即可使用如下密技: SHIFTV--追踪 SHIFTX--瞬间移动 CTRLI--无敌 CTRLSHIFTN--完成任务 CtrlShiftX--敌人全爆 选关密码: MISSION2: 4JJXB …
K11375 突击战[Commando War,UVa11729]
题目描述
你有N个部下,每个部下需要独立完成一项任务。第i个部下需要你花费Bi分钟交代任务,然后他会立刻独立、无间断地执行Ji分钟后完成任务。你需要选择交代任务的顺序,使得所有任务尽早执行完毕(即最后一个执行完的任务应尽早…