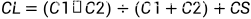前面我们了解了晶振的结构，也了解了晶振的模型，这一节就来看看晶振是如何起振的。

    皮尔斯晶体振荡器

    目前工作中用得最多的就是皮尔斯晶体振荡器，也就是下面这个结构。

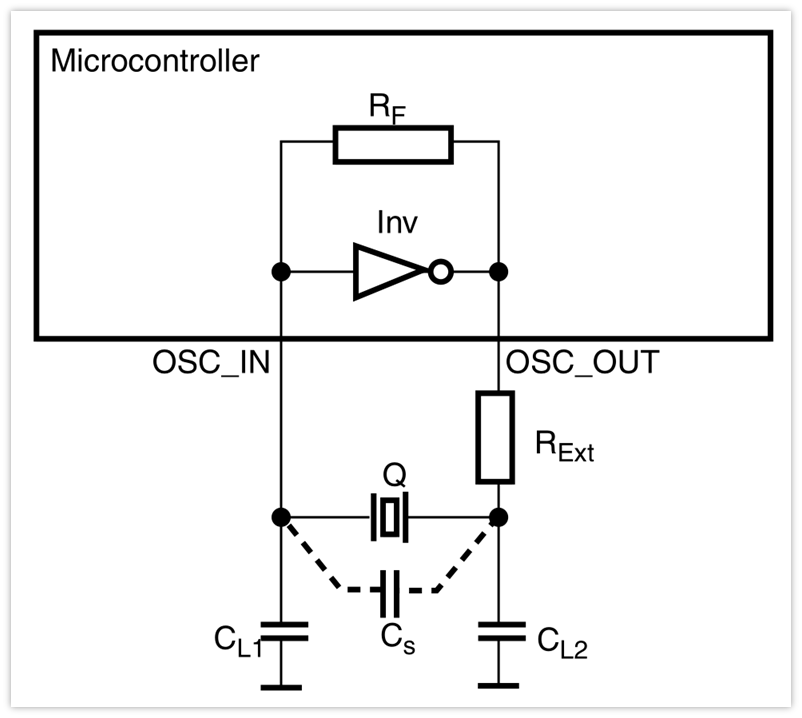
    CL1，CL2为匹配电容，Rext通常为串联的几百欧姆电阻（有时也不加）。上面这个结构可能看着不是很熟悉，我们把它转换一下，变成下面这个就熟悉些。

    上图中把RF忽略掉了，如果用过无源晶振的话，应该知道这个RF的阻值一般是很大的，兆欧姆级别，其作用主要是为了给反相放大器一个合适偏置。就像我们模电里面的三极管电路，其工作时都需要合适的直流偏置，这里我们先忽略掉。

    结合上一章节说的晶振的等效电路

    我估计有人看到这里就跑了，这一坨是什么东西，搞这么复杂？其实没那么难，这里面所有的器件，除了反相放大器外，都是基本元器件，反而是更容易分析的。

    不过在这之前呢？我们还是插播一个知识点，那就是起振条件。因为只有搞懂了起振条件，我们才能知其然并且知其所以然，先理论分析，然后用仿真去验证，如此更爽。

    起振条件

    起振条件有两个：相位和环路增益

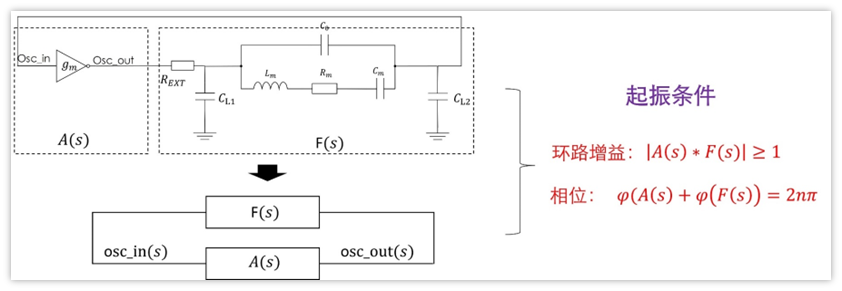
    上图中将反相放大器的传递函数用A(s)表示，晶振及其匹配电路打包一起，其传递函数看作F(s)。

    当环路增益大于1时，说明输入信号在环路中逛一圈后又送到输入端，信号幅度比原来更大

    相位为2nπ，说输入信号在电路中逛一圈后，相位与原本的输入信号完全相同，因此输入信号被完美的加强了。

    两者结合，就形成了这样的情况：信号经过反复放大后，不断增大，最终就是我们看到那样。

    当环路中的信号幅度增大到一定程度后，振荡器中的有源器件（晶振电路中的反相器）存在的非线性会限制幅度的继续增加，使得振荡器的输出达到稳定。通俗说就是振荡的幅值肯定超不过电源电压。

    也就是说，只要满足那两个条件，再小的信号，经过环路的无限循环（输入信号Vin逛一圈变成更大的Vin，然后再逛一圈变成更更大的Vin，然后再逛一圈。。。），最终输出幅度总会起来。

    尽管我们没有专门提供对应频率的输入信号Vin，但是电路中总会有噪声，比如白噪声就是全频段的，虽然信号很小，但是因为电路的这个不断加强的特性，所以最终一定有输出信号。也就是说，起振是必然的。

    总之，起振要满足这两个条件：

    关于晶振起振，有一个准则叫巴克毫森稳定性准则，想深入去看的同学可以去查查。

    起振电路分析

    上期说完了起振条件，那我们继续分析前面的电路，先看相位。

    相位

    相位需要满足2nπ，显然，n不可能等于0，等于零意外着完全没有相移，电路中有反相放大器，已经相移了π，也就是180°。所以最可能的就是晶振那一坨电路也让信号相移180度，整体凑够360°，也就是2π。

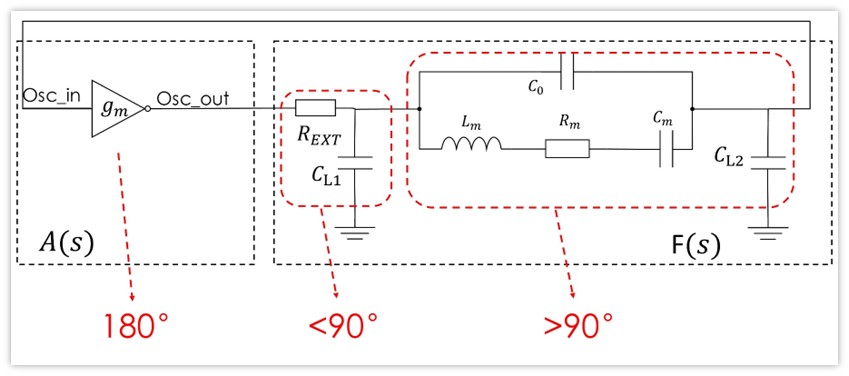
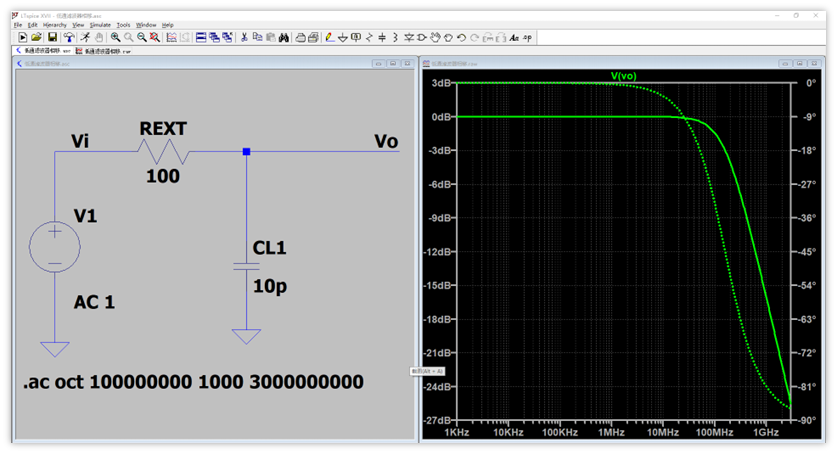
    Rext和匹配电容CL1构成一个低通滤波器，带来的相移是小于90°的，这应该很容易知道，下图是Rext=100Ω，CL1=10p的低通滤波器的幅频曲线，可以看到，输入与输出的相位差是：0°~90°，输出滞后输入。

    Rext和匹配电容CL1带来的相移是小于90°，那么晶振与CL2带来的相移必须大于90°，如此才能凑够180°。

    那么什么时候晶振与CL2带来的相移是大于90°的呢？答案是必须晶振等效电路整体呈电感性才有可能。

    晶振等效电路有三种元器件构成，电阻，电感，电容，其总的等效阻抗可能有三种情况：呈阻性，呈容性，呈感性。

    如果从数学角度来看，晶振总阻抗公式化简之后总能写成一个复数的形式，包含实数和虚数的表达式：Z=R+jX。其中R是电阻分量，X为电抗分量。
    当X=0：Z=R，整体呈阻性
    当X>0：Z=R+jX，整体呈感性
    当X<0：Z=R+jX，整体呈容性。

    下面分别看下三种情况下，晶振与匹配电容CL2的相位情况。

    阻抗公式算出来肯定是一大坨的，就不列了，我们直接看仿真，这样更为直观（电阻100只是象征性取值，可以取其它的，不影响结果，电容值也是）

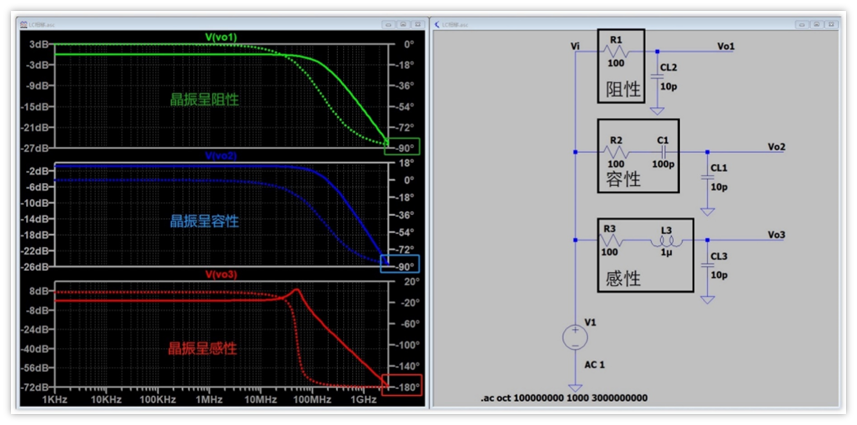
    可以看到，只有晶振在呈感性的时候，相移才能大于90°，其相移范围是：0~180°。

    综上所述，晶振工作时呈感性。那么，晶振呈感性的频率范围是多少呢？

    晶振呈感性频率范围

    阻抗呈感性的频率范围，列出晶振的总阻抗公式就好了。

    理论上说，总阻抗是个复数，我们可以把它化简成实部和虚部，虚部大于0时，即表示晶振呈感性。不过这也太费劲，还是直接搞一个实际的晶振参数看看。

    大多数晶振都是没有给出Lm，Rm，Cm参数的，不过我查到爱普生的晶振有写出来，比如下面这款25Mhz的晶振。

    可以看到，Rm最大为80Ω，动态电容Cm=1.94fF，动态电感Lm=20.91mH，静态电容C0=0.6pF。

    我们直接用这些参数，采用LTspice仿真的方式画出阻抗曲线吧。

    仿真的原理很简单，给一个1A的电流源，那么Vz的电压就是阻抗乘以电流，电流为1A，那么Vz的值就是阻抗值，因此，图中左边的dB幅度值就是阻抗值。相位表示电压超前电流的相角，因此，如果相位大于0，表示整体阻抗是感性，若小于0，表示整体阻抗是容性的。

    从图中可以看出，两个尖之间的区域，相角大于0，就是呈感性的区域，晶体振荡频率25Mhz正好处于这一区域。

    从图上看，两个冒尖的频率分别是24.988623Mhz，25.028984Mhz，很容易猜到，两个冒尖的频点这么特殊，应该是串联谐振点和并联谐振点。

    我们可以验证下，分别计算下串联谐振和并联谐振。

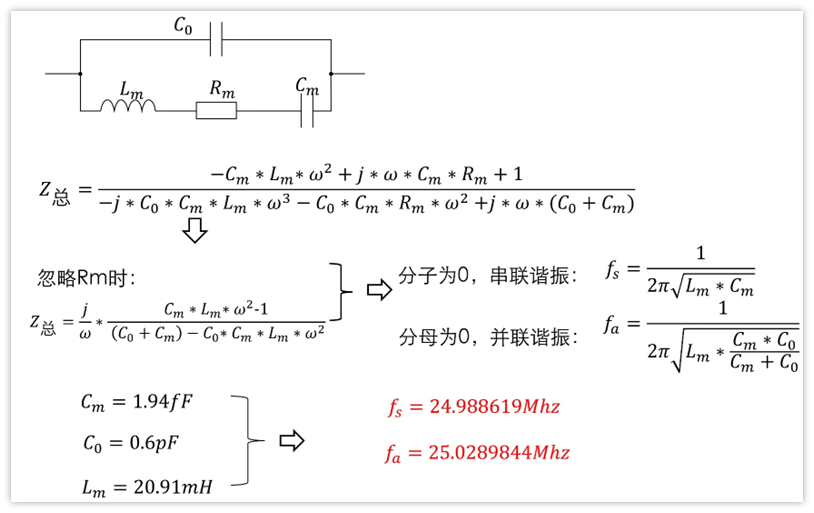
    计算值fs=24.988619Mhz，仿真图读值fs=24.988623Mhz
    计算值fa=25.0289844Mhz，仿真图读值fa=25.028984Mhz

    可以看到，可以说完全一致。

    因此，晶体工作频率范围为：

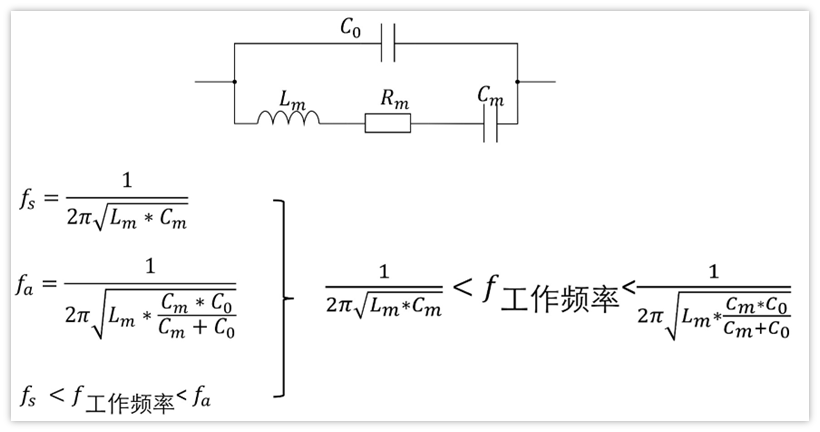
    当    然，以上只是说晶振实际工作的频率处于这个之间，并不是说实际工作时频率变化范围有这么大，衡量稳定度是有个参数叫频偏，注意不要误解。

    小结

    本节就写到这里了，暂时只说明了相位关系，其实还有些问题没搞清楚。

    比如这个：我们都知道实际应用中，改变匹配电容，可以微调晶振工作频率，所以实际工作频率跟匹配电容肯定有关系，应该是有关系式的。具体关系式我在一些资料中已经看到了，不过只知道个结果吧，还没搞清楚咋来的，暂时就先放着吧。

    以上就是本期内容了，如果有问题，欢迎留言指出。