文章目录
- 第七章 集成学习
- 7.1个体和集成
- 7.2Boosting和AdaBoost
- 7.3Bagging和随机森林
- 7.3.1Bagging
- 7.3.2随机森林
- 7.4结合策略
- 7.4.1平均法
- 7.4.2投票法
- 7.4.3学习法
- 7.6实验:Adaboost
第七章 集成学习
7.1个体和集成
集成学习通过构建并结合多个学习器来完成学习任务,有时也被称为多分类器系统
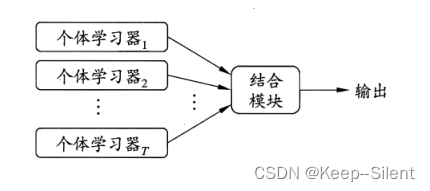
如在二分类中,采用个体学习器少数服从多数原则,进行预测

个体学习器应满足“好而不同”:
- 个体学习器不同:避免集成不起作用
- 个体学习器有一定的准确率:避免集成起副作用
7.2Boosting和AdaBoost
Boosting是一族可将弱学习器提升为强学习器的算法.这族算法的工作机制类似:先从初始训练集训练出一个基学习器,再根据基学习器的表现对训练样本分布进行调整,使得先前基学习器做错的训练样本在后续受到更多关注,然后基于调整后的样本分布来训练下一个基学习器;如此重复进行,直至基学习器数目达到事先指定的值T,最终将这T个基学习器进行加权结合.其中最著名的代表是AdaBoost
AdaBoost是基于“加性模型”,即基学习器的线性组合 H ( x ) = ∑ t = 1 T α t h t ( x ) H(\boldsymbol{x})= \sum_{t=1}^{T} \alpha_{t}h_{t} (\boldsymbol{x}) H(x)=t=1∑Tαtht(x)
算法:

7.3Bagging和随机森林
为获得好的集成,我们同时还希望个体学习器不能太差.如果采样出的每个子集都完全不同*,则每个基学习器只用到了一小部分训练数据,甚至不足以进行有效学习,这显然无法确保产生出比较好的基学习器.为解决这个问题,我们可考虑使用相互有交叠的采样子集.
7.3.1Bagging
基于自组采样法第二章 模型评估和选择 2.2.3自助法

算法描述:

简单来说,我们可采样出T个含m个训练样本的采样集,然后基于每个采样集训练出一个基学习器,再将这些基学习器进行结合.这就是Bagging 的基本流程.
在对预测输出进行结合时,Bagging 通常对分类任务使用简单投票法,对回归任务使用简单平均法.若分类预测时出现两个类收到同样票数的情形,则最简单的做法是随机选择一个,也可进一步考察学习器投票的置信度来确定最终胜者
自助采样过程还给Bagging带来了另一个优点:由于每个基学习器只使用了初始训练集中约63.2%的样本,剩下约36.8%的样本可用作验证集来对泛化性能进行“包外估计” 为此需记录每个基学习器所使用的训练样本.令 D t D_t Dt:表示 h t h_t ht实际使用的训练样本集,令 H o o b ( x ) H^{oob}(x) Hoob(x)表示对样本 x x x的包外预测,即(仅考虑那些未使用 x x x训练的基学习器在 x x x上的预测,有 H o o b ( x ) = arg max y ∈ Y ∑ t = 1 T I ( h t ( x ) = y ) ⋅ I ( x ∉ D t ) H^{\boldsymbol{oob}}(\boldsymbol{x})= \arg\max_{y\in\mathcal{Y}} \sum_{t=1}^T\mathbb{I}(h_t(\boldsymbol{x})=y) \cdot\mathbb{I}(\boldsymbol{x}\notin D_t) Hoob(x)=argy∈Ymaxt=1∑TI(ht(x)=y)⋅I(x∈/Dt)
则Bagging泛化误差的包外估计为 ϵ o o b = 1 ∣ D ∣ ∑ ( x , y ) ∈ D I ( H o o b ( x ) ≠ y ) \epsilon^{oob}= \frac1{|D|} \sum_{(\boldsymbol{x},y)\in D} \mathbb{I}(H^{oob} (\boldsymbol{x})\neq y) ϵoob=∣D∣1(x,y)∈D∑I(Hoob(x)=y)
7.3.2随机森林
随机森林(Random Forest,简称RF)是 Bagging 的一个扩展变体.RF在以决策树为基学习器构建Bagging集成的基础上,进一步在决策树的训练过程中引入了随机属性选择.具体来说,传统决策树在选择划分属性时是在当前结点的属性集合(假定有d个属性)中选择一个最优属性;而在RF中,对基决策树的每个结点,先从该结点的属性集合中随机选择一个包含k个属性的子集,然后再从这个子集中选择一个最优属性用于划分.这里的参数k控制了随机性的引入程度:若令k = d,则基决策树的构建与传统决策树相同;若令k= 1,则是随机选择一个属性用于划分;一般情况下,推荐值 k = log 2 d k = \log_2 d k=log2d
7.4结合策略
7.4.1平均法
简单平均法: H ( x ) = 1 T ∑ i = 1 T h i ( x ) H(\boldsymbol{x})=\frac1T\sum_{i=1}^Th_i(\boldsymbol{x}) H(x)=T1i=1∑Thi(x)
加权平均法: H ( x ) = ∑ i = 1 T w i h i ( x ) ( w i ⩾ 0 , ∑ i = 1 T w i = 1 ) H(\boldsymbol{x})=\sum_{i=1}^Tw_ih_i(\boldsymbol{x}) \;(w_i\geqslant0,\sum_{i=1}^Tw_i=1) H(x)=i=1∑Twihi(x)(wi⩾0,i=1∑Twi=1)
加权平均法的权重一般是从训练数据中学习而得,现实任务中的训练样本通常不充分或存在噪声,这将使得学出的权重不完全可靠.加权学习法不一定优于简单平均法。
7.4.2投票法
对分类任务来说,学习器h将从类别标记集合 { c 1 , c 2 , . . . , c N } \{c_1,c_2,...,c_N\} {c1,c2,...,cN}中预测出一个标记,最常见的结合策略是使用投票法.为便于讨论,我们将 h i h_i hi在样本 x x x上的预测输出表示为一个N维向量 ( h i 1 ( x ) ; h i 2 ( x ) ; … ; h i m ( x ) ) (h_i^1(\boldsymbol{x}); h_i^2(\boldsymbol{x}); \ldots; h_i^m(\boldsymbol{x})) (hi1(x);hi2(x);…;him(x)),其中 h i h ( x ) h_i^h(x) hih(x)是 h i h_i hi在类别标记 c j c_j cj上的输出.
绝对多数投票法: H ( x ) = { c j , i f ∑ i = 1 T h i j ( x ) > 0.5 ∑ k = 1 m ∑ i = 1 T h i k ( x ) r e j e c t , o t h e r w i s e . H\left(\boldsymbol{x}\right)= \left\{\begin{array}{l}c_{j},&\displaystyle \mathrm{~if~}\sum_{i=1}^{T}h_{i}^{j} \left(\boldsymbol{x} \right)>0.5\sum_{k=1}^{m} \sum_{i=1}^{T}h_{i}^{k} \left(\boldsymbol{x}\right)\\ \mathrm{reject},& \mathrm{~otherwise}. \end{array}\right. H(x)=⎩ ⎨ ⎧cj,reject, if i=1∑Thij(x)>0.5k=1∑mi=1∑Thik(x) otherwise.
即若某标记得票过半数,则预测为该标记;否则拒绝预测.
相对多数投票法: H ( x ) = c arg max j ∑ i = 1 T h i j ( x ) H(\boldsymbol{x})=c_{\arg\max_j \sum_{i=1}^T h_i^j(\boldsymbol{x})} H(x)=cargmaxj∑i=1Thij(x)
即预测为得票最多的标记.
加权投票法: H ( x ) = c argmax j ∑ i = 1 T w i h i j ( x ) H(\boldsymbol{x})=c_{\underset{j}{\operatorname*{argmax}}\sum_{i=1}^Tw_ih_i^j(\boldsymbol{x})} H(x)=cjargmax∑i=1Twihij(x)
即加上了权重
7.4.3学习法
当训练数据很多时,一种更为强大的结合策略是使用“学习法”,即通过另一个学习器来进行结合.Stacking 是学习法的典型代表.这里我们把个体学习器称为初级学习器,用于结合的学习器称为次级学习器或元学习器.

7.6实验:Adaboost
先导入数据集,并显示部分数据
from numpy import *
import numpy as npdef loadDataSet(name):dataMatrix = []; classLabels = []fr = open(name)for line in fr.readlines():lineArr = line.strip().split()dataMatrix.append(np.array([float(x) for x in lineArr[:-1]]))classLabels.append(float(lineArr[-1]))return np.array(dataMatrix), np.array(classLabels)
dataMatrix, classLabels=loadDataSet('07horseColicTraining.txt')
print(dataMatrix[:5])
print(classLabels[:5])
[[ 2. 1. 38.5 66. 28. 3. 3. 0. 2. 5. 4. 4. 0. 0. 0. 3. 5. 45. 8.4 0. 0. ][ 1. 1. 39.2 88. 20. 0. 0. 4. 1. 3. 4. 2. 0. 0. 0. 4. 2. 50. 85. 2. 2. ][ 2. 1. 38.3 40. 24. 1. 1. 3. 1. 3. 3. 1. 0. 0. 0. 1. 1. 33. 6.7 0. 0. ][ 1. 9. 39.1 164. 84. 4. 1. 6. 2. 2. 4. 4. 1. 2. 5. 3. 0. 48. 7.2 3. 5.3][ 2. 1. 37.3 104. 35. 0. 0. 6. 2. 0. 0. 0. 0. 0. 0. 0. 0. 74. 7.4 0. 0. ]]
[-1. -1. 1. -1. -1.]
stumpClassify是一个单层决策树,通过阈值比较分为两类:-1和1
- threshIneq是lt(less)时将小于等于阈值的数据分为-1,其余为1
- threshIneq是gt(greater)时将大于阈值的数据分为-1,其余为1
threshIneq姑且称为阈值划分方式
并测试这个函数
def stumpClassify(dataMatrix,attribute,threshVal,threshIneq):#just classify the dataretArray = ones((shape(dataMatrix)[0],1))if threshIneq == 'lt':retArray[dataMatrix[:,attribute] <= threshVal] = -1.0else:retArray[dataMatrix[:,attribute] > threshVal] = -1.0return retArrayretArray=stumpClassify(dataMatrix,1,5,'lt')
print(retArray[:5])
retArray=stumpClassify(dataMatrix,1,5,'gt')
print(retArray[:5])[[-1.][-1.][-1.][ 1.][-1.]]
[[ 1.][ 1.][ 1.][-1.][ 1.]]
buildStump将在属性、阈值、阈值划分方式三者中,找到一组误差最小的划分组合
buildStump将生成一个单层决策树,伪代码如下:
for 属性 in 所有属性:for 阈值 in 最小到最大的step等分阈值:for 阈值划分方式 in ['lt','gt']:计算误差如误差小于当前最小误差则更新
def buildStump(dataMatrix,classLabels,D):n,m = shape(dataMatrix)dataMatrix=mat(dataMatrix)bestStump={}minError=infstep=10 #设置阈值个数for attribute in range(m):minValue=dataMatrix[:,attribute].min()maxValue=dataMatrix[:,attribute].max()stepSize=(maxValue-minValue)/stepfor threshVal in np.arange(minValue-stepSize,maxValue+stepSize*2,stepSize):for threshIneq in ['lt','gt']:predictVal=stumpClassify(dataMatrix,attribute,threshVal,threshIneq)predictVal=predictVal[:,0]errArr = mat(ones((n,1)))errArr[predictVal == classLabels] = 0predictError = D.T*errArrpredictError=predictError[0,0]# print("attribute %d, thresh %.2f, thresh ineqal: %s, the weighted error is %.3f" % (attribute, threshVal, threshIneq, predictError))if predictError < minError:minError = predictErrorbestClasEst = predictVal.copy()bestStump['attribute'] = attributebestStump['threshVal'] = threshValbestStump['threshIneq'] = threshIneqbestStump['minError'] = minErrorreturn bestStump,minError,bestClasEstn,m = shape(dataMatrix)
D = mat(ones((n,1))/n)
bestStump,minError,bestClasEst=buildStump(dataMatrix,classLabels,D)
print(bestStump)
print('minError',minError){'attribute': 9, 'threshVal': 3.0, 'threshIneq': 'gt', 'minError': 0.28428093645484953}
minError,0.28428093645484953
完成核心代码adaBoostTrainDS,训练numIt个单层决策树
伪代码:
for i in range(numIt):利⽤buildStump()函数找到最佳的单层决策树将最佳单层决策树加⼊到单层决策树数组计算alpha计算新的权重向量D更新累计类别估计值
def adaBoostTrainDS(dataArr,classLabels,numIt=10):weakClassArr = []m = shape(dataArr)[0]D = mat(ones((n,1))/n) #init D to all equalaggClassEst = mat(zeros((n,1)))for i in range(numIt):bestStump,error,classEst = buildStump(dataArr,classLabels,D)#build StumpclassEst=mat(classEst).Talpha = float(0.5*log((1.0-error)/max(error,1e-16)))bestStump['alpha'] = alpha weakClassArr.append(bestStump) expon = multiply(-1*alpha*mat(classLabels).T,classEst) D = multiply(D,exp(expon)) D = D/D.sum() aggClassEst += (alpha*classEst) aggErrors = multiply(sign(aggClassEst) != mat(classLabels).T,ones((n,1)))errorRate = aggErrors.sum()/nif errorRate == 0.0: breakreturn weakClassArrweakClassArr=adaBoostTrainDS(dataMatrix,classLabels)
for weakClass in weakClassArr:print(weakClass)
{'attribute': 9, 'threshVal': 3.0, 'threshIneq': 'gt', 'minError': 0.28428093645484953, 'alpha': 0.4616623792657674}
{'attribute': 17, 'threshVal': 52.5, 'threshIneq': 'gt', 'minError': 0.3472332812161393, 'alpha': 0.3156114929327882}
{'attribute': 3, 'threshVal': 55.199999999999996, 'threshIneq': 'gt', 'minError': 0.35750587621595387, 'alpha': 0.29310293594973225}
{'attribute': 18, 'threshVal': 53.400000000000006, 'threshIneq': 'lt', 'minError': 0.3922730925346517, 'alpha': 0.2188836769233133}
{'attribute': 15, 'threshVal': 0.0, 'threshIneq': 'lt', 'minError': 0.4062170817974291, 'alpha': 0.18981304702807467}
{'attribute': 5, 'threshVal': 2.0000000000000004, 'threshIneq': 'gt', 'minError': 0.413744417033253, 'alpha': 0.17425370493717318}
{'attribute': 5, 'threshVal': 0.0, 'threshIneq': 'lt', 'minError': 0.43076646870832686, 'alpha': 0.13936233333702944}
{'attribute': 7, 'threshVal': 1.1999999999999997, 'threshIneq': 'gt', 'minError': 0.41936713025879085, 'alpha': 0.16268596062198426}
{'attribute': 4, 'threshVal': 28.799999999999997, 'threshIneq': 'lt', 'minError': 0.4346242541793776, 'alpha': 0.1315043363205097}
{'attribute': 12, 'threshVal': 1.2, 'threshIneq': 'lt', 'minError': 0.44328851139912123, 'alpha': 0.11391315330833288}
经过adaBoostTrainDS算法,可训练出多个个体学习器weakClassArr(如上,训练了十个个体学习器)
为了进行评判学习器:
- 完成adaClassify函数(用weakClassArr进行预测)
- 完成adaAcc函数:得到某数据集的预测准确度
def adaClassify(datToClass,classifierArr):dataMatrix = mat(datToClass)n,m = shape(dataMatrix)aggClassEst = mat(zeros((n,1)))for i in range(len(classifierArr)):classEst = stumpClassify(dataMatrix, classifierArr[i]['attribute'],\classifierArr[i]['threshVal'],\classifierArr[i]['threshIneq'])#call stump classifyaggClassEst += classifierArr[i]['alpha']*classEstreturn sign(aggClassEst)aggClassEst=adaClassify(dataMatrix,weakClassArr)def adaAcc(dataMatrix,classLabels,weakClassArr):n,m = shape(dataMatrix)predict=adaClassify(dataMatrix,weakClassArr)accArr=[(1 if predict[i,0]==classLabels[i] else 0) for i in range(n)]return sum(accArr)/nacc=adaAcc(dataMatrix,classLabels,weakClassArr)
print(acc)
0.7591973244147158
先分别导入训练集和测试集
再用训练集分别训练出含有不同个数的集成学习器
最后用数据集进行对这些集成学习器进行测试
trainData,trainLabel=loadDataSet('07horseColicTraining.txt')
testData,testLabel=loadDataSet('07horseColicTest.txt')
classNumbers=[1,10,30,50,100,500]
print('|classNumber|train Acc|test Acc|')
print('|--|--|--|')
for classNumber in classNumbers:weakClassArr=adaBoostTrainDS(dataMatrix,classLabels,classNumber)trainAcc=adaAcc(trainData,trainLabel,weakClassArr)testAcc=adaAcc(testData,testLabel,weakClassArr)print('|%d|%.2f%%|%.2f%%|'%(classNumber,trainAcc*100,testAcc*100))| classNumber | train Acc | test Acc |
|---|---|---|
| 1 | 71.57% | 73.13% |
| 10 | 75.92% | 76.12% |
| 30 | 78.93% | 77.61% |
| 50 | 79.93% | 79.10% |
| 100 | 82.27% | 77.61% |
| 500 | 84.62% | 76.12% |
通过此表格可以看出,当基学习器少的时候,随着学习器个数的增加,对于训练数据和测试数据,集成学习器的预测准确度都不断提高。
当基学习器过多的时候,集成学习器对训练数据的预测准确度仍在提高,但是对测试数据的预测准确度不断降低,即出现了过拟合的情形。
结论:
- 多个个体学习器结合形成的集成学习器确实比一个学习器更优
- 学习器数量的选择不应过少或过多。过少则还有提升空间,过多则会过拟合