目录
第1章 损耗与损耗系数
1.1 损耗
1.2 吸收系数
1.3 吸收光谱
第2章 增益与增益系数
2.1 增益
2.2 增益饱和
2.3 增益谱线
2.4 单位增益带宽
第3章 自激振荡
3.1 什么是自激振荡
3.2 增益系数与损耗系数的关系
3.3 光学谐振腔与自激震荡
第1章 损耗与损耗系数
1.1 损耗

光在介质透明介质中传播时,光的强度随传播距离(穿透深度)而衰减的现象称为光的吸收。
光的吸收遵循吸收定律(比尔-朗伯定律)。
1.2 吸收系数
吸光系数指吸光物质在单位浓度及单位厚度时的吸光度。
常用两种 表示方法:摩尔吸光系数和百分吸光系数。
摩尔吸光系数是指物质对某波长的光的吸收能力的量度。指一定波长时,溶液的浓度为1 mol/L,光程为1cm时的吸光度值,用ε或EM表示。ε越大,表明该溶液吸收光的能力越强,相应的分光度法测定的灵敏度就越高。 在一定条件(单色光波长、溶 剂、温度等)下,吸光系数是物质的特性常数,可作为物质定性的依据。
根据比尔定律,吸光度A与吸光物质的浓度c和吸收池光程长b的乘积成正比。当c的单位为g/L,b的单位为cm时,则 A = abc,比例系数a称为吸收系数;当c的单位为mol/L,b的单位为cm时,则 A = εbc,比例系数ε称为摩尔吸收系数,数值上ε等于a与吸光物质的摩尔质量的乘积。吸收系数α与吸光系数k的关系:α=4*k*π/λ。
光的波长不同,其吸光系数也不同。单色光的纯度越高,摩尔吸光系数越大。
1.3 吸收光谱
吸收光谱(absorption spectrum)是指物质吸收光子,从低能级跃迁到高能级而产生的光谱。
吸收光谱可是线状谱或吸收带。研究吸收光谱可了解原子、分子和其他许多物质的结构和运动状态,以及它们同电磁场或粒子相互作用的情况。
吸收光谱是指包含各种波长的光被吸收后剩下的频率的光的谱线。
吸收光谱又名吸收曲线。不同波长光对工作物质作用不同,吸收强度也不同。如下图所示:
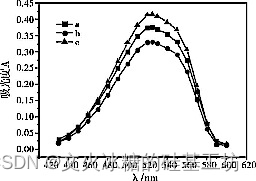

处于基态和低激发态的原子或分子吸收具有连续分布的某些波长的光而跃迁到各激发态,形成了按波长排列的暗线或暗带组成的光谱。
吸收光谱是温度很高的光源发出来的白光,通过温度较低的蒸气或气体后产生的,如果让高温光源发出的白光,通过温度较低的钠的蒸气就能生成钠的吸收光谱。光谱背景是明亮的连续光谱。在钠的标识谱线的位置上出现了暗线。通过大量实验观察总结,每一种元素的吸收光谱里暗线的位置与其明线光谱的位置互相重合。即每种元素所发射的光频率与其所吸收的光频率相同。
纯白光为一连续的从红色到紫色的光谱,但当白光穿过一个有色宝石,一定颜色或波长可被宝石所吸收,这导致该白光光谱中有一处或几处间断,这些间断以暗线或暗带形式出现。许多宝石显示出在可见光谱中吸收带或线的特征样式,其完整的样式也即“吸收光谱”。
高温物体发出的白光(其中包含连续分布的一切波长的光)通过物质时,某些波长的光被物质吸收后产生吸收光谱。例如,让弧光灯发出的白光通过温度较低的钠气(在酒精灯的灯心上放一些食盐,食盐受热分解就会产生钠气),然后用分光镜来观察,就会看到在连续光谱的背景中有两条挨得很近的暗线,就是钠原子的吸收光谱。各种原子的吸收光谱中的每一条暗线都与该原子的发射光谱中的一条明线相对应。表明低温气体原子吸收的光,就是这种原子在高温时发出的光。因此,吸收光谱中的暗线,就是原子的特征谱线。
第2章 增益与增益系数
2.1 增益


随着光强度的增加,单位时间释放的光的粒子数量在增加,因此,高能态上的反转粒子会减少。随着反转粒子会减少,单位时间释放的光的粒子数量也会减少,增益系数就会下降。因此,增益系数不能一直增大 。

2.2 增益饱和
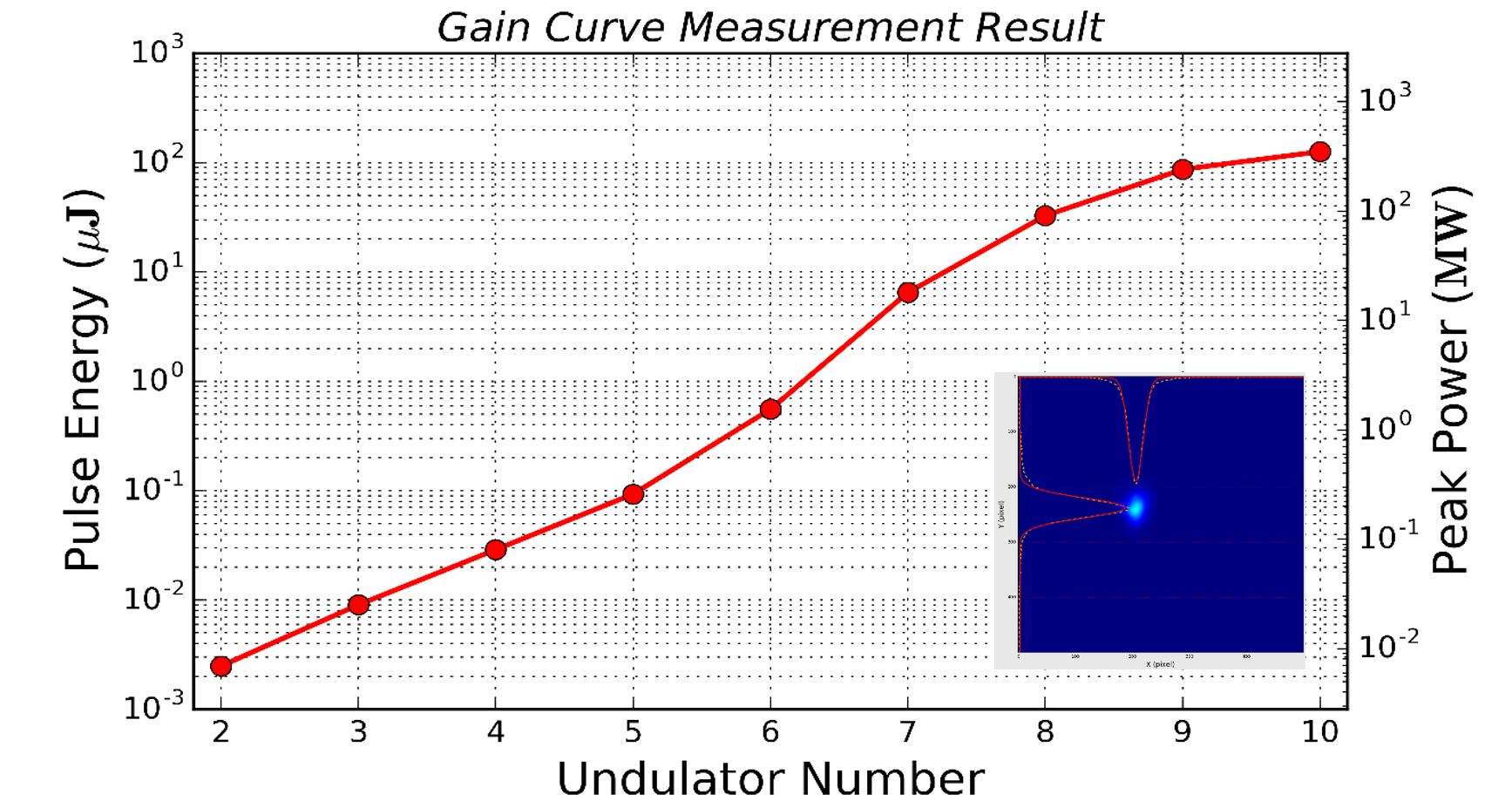
在小信号增益下(也就是光强小时)增益系数G随着入射光强的增大而迅速增大;也就是输出光与输入光的强度的比值随着输入光强度的增大而增大。
但是当输入光强增大到一定的程度后,增益系数G随光强的增大而基本不变,这种现象为增益饱和。
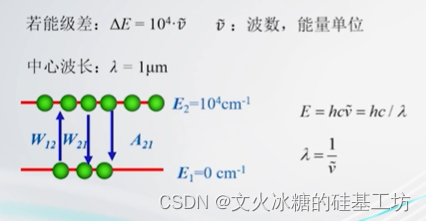
2.3 增益谱线
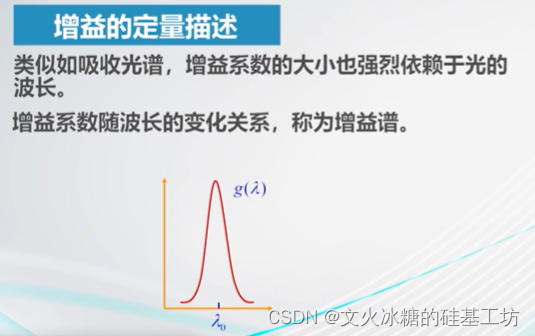
相同的工作物质,对不同频率的光的增益是不相同的,对有些频率的光是增强的,对有些频率的光是不增加的,直接被吸收掉了。 在上图中,工作物质对频率f0的光的增益是最大的,即对f0的光的增强能力最大。由于光谱是连续的,因此,增益光谱也是有带宽的。
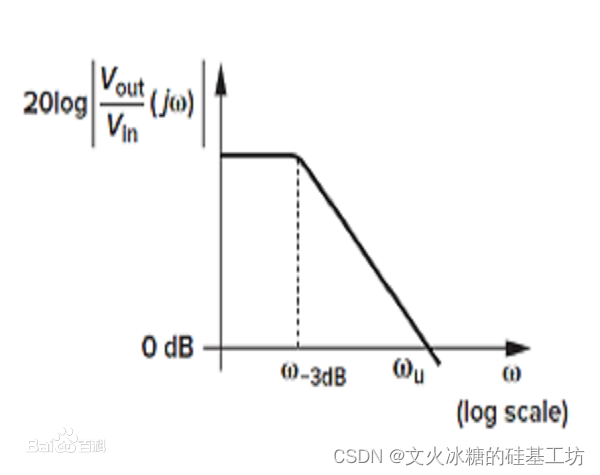
2.4 单位增益带宽
单位增益带宽定义为,运放的闭环增益为1倍条件下,将一个频率可变恒幅正弦小信号输入到运放的输入端,随着输入信号频率不断变大,输出信号增益将不断减小,当从运放的输出端测得闭环电压增益下降3db(或是相当于运放输入信号的0.707)时,所对应的信号频率乘以闭环放大倍数1所得的增益带宽积。
第3章 激光器的自激振荡
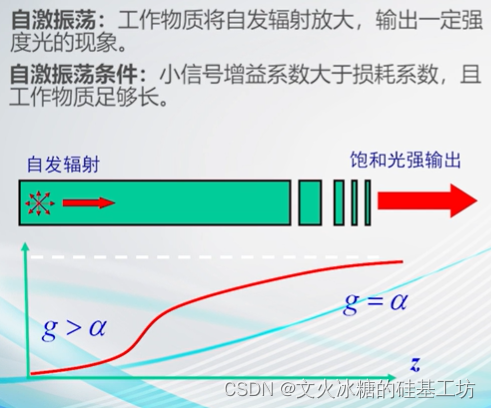
3.2 什么是自激振荡
自激振荡是指不外加激励信号而自行产生的恒稳和持续的振荡。
如果在放大器的输入端不加输入信号,输出端仍有一定的幅值和频率的输出信号,这种现象就是自激振荡。
从数学的角度出发,它是一种出现于某些非线性系统中的一种自由振荡。一个典型例子是范达波尔(Van der Pol)方程所描述的系统,方程形式为 mx¨-f(1-x2)x·-kx=0 (m>0, f>0, k>0)。 其中x·和x¨为变量x的一阶和二阶导数。分析表明:当x的值很小时,阻尼f是负的,因而运动发散;当x的值很大时,阻尼f是正的,因而运动衰减。所以,不管由什么初始条件出发,系统运动都趋向于一个持续振荡,即自激振荡。

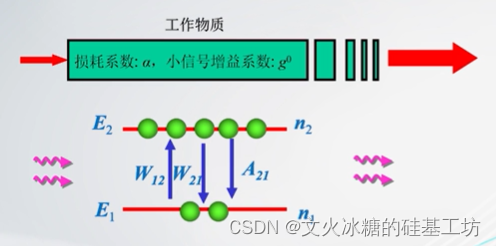
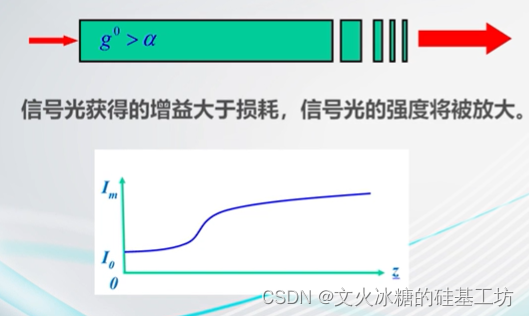
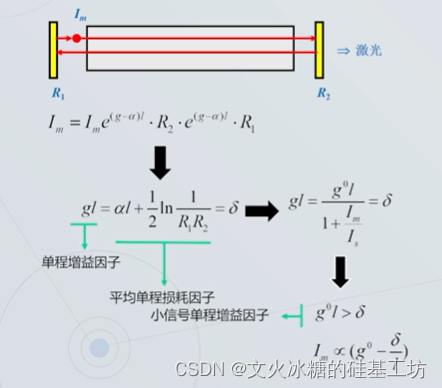
3.2 增益系数与损耗系数的关系


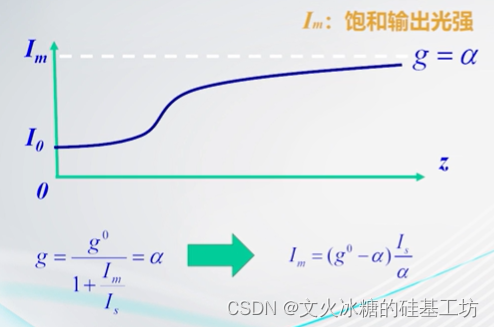
3.3 光学谐振腔与自激震荡
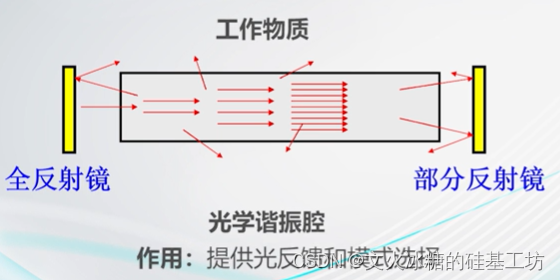

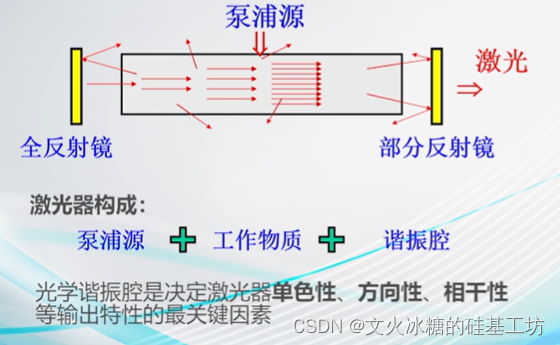
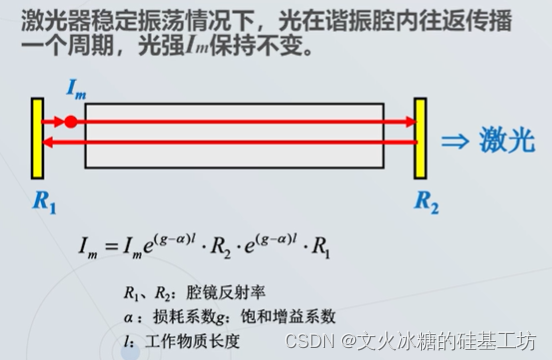

![[激光原理与应用-28]:《激光原理与技术》-14- 激光产生技术 - 激光的主要参数与指标](https://img-blog.csdnimg.cn/img_convert/9b0726ec89450c1fc978ba2757c1ef43.jpeg)
![[激光原理与应用-17]:《激光原理与技术》-3- 激光的产生技术 与原理 - 微观粒子、能级、电子、光子、受激辐射](https://img-blog.csdnimg.cn/32863b14203449b6b0adf6a134575d96.png)
![[激光原理与应用-30]:典型激光器 -2- 气体激光器 (连续激光器)](https://img-blog.csdnimg.cn/img_convert/0b1d948bcfce8c23de2c38ced93af4b9.jpeg)
![[激光原理与应用-32]:典型激光器 -4- 半导体泵浦固体激光器](https://img-blog.csdnimg.cn/img_convert/7ce23bca979deb3ba3155dd033525df1.png)