1.问题描述
2000以内的不小于4的正偶数都能够分解为两个素数之和(即验证歌德巴赫猜想对2000以
内的正偶数成立)。
2.问题分析
根据问题描述,为了验证歌德巴赫猜想对2000以内的正偶数都是成立的,要将整数分解
为两部分,然后判断分解出的两个整数是否均为素数。若是,则满足题意,否则应重新进行
分解和判断。
针对该问题,我们可以给定如下的输入和输出限定。
输入时:每行输入一组数据,即2000以内的正偶数n,一直输入到文件结束符为止。
输出时:输出n能被分解成的素数a和b。如果不止一组解,则输出其中a最小的那组解。
当然,读者可以根据实际的需要规定不同的输入和输出形式。
输入示例:
4
6
8
10
12
输出示例:
2 2
3 3
3 5
3 7
5 7
3.算法设计
本问题我们可以采用函数来解决。
(1)fun(n)函数判断输入的n值是否为素数
定义一个函数,函数名设为fun,在其中判断传进来的形参——设为n(n≥2),是否为素
数,如果是素数则返回1,否则返回0。在判断是否为素数时,可以采用5.1节中介绍的方法。
需要注意的是,在所有偶数中,只有2是唯一的素数。因此,在函数fun()中,可以分为以下4
种情况来判断:
·n=2,是素数,返回1。
·n是偶数,不是素数,返回0。
·n是奇数,不是素数,返回0。
·n≠2,是素数,返回1。
(2)guess(n)函数用于验证哥德巴赫猜想
由于我们已经对输出做了限定,即当输出结果时,如果有多组解,则输出a最小的那组
解。显然,对每个读入的数据n,a必然小于或等于n//2,因此,定义循环变量i,使其从2~n/2
进行循环,每次循环都做如下判断:fun(i) and fun(n-i)是否为1。
如果fun(i) and fun(n-i)=1,则表示fun(i)=1同时fun(n-i)=1。由fun()函数的定义可知,此时i
和n-i都为素数,又由于i是从2~n/2按由小到大的顺序来迭代的,因此,(i,n-i)是我们求出
的一组解,且该组解必然是所有可能解中a值最小的。
还需要注意的是,由于除了2以外的偶数不可能是素数,因此,i值的可能取值只能是2和
所有的奇数。
4.确定程序框架
(1)程序主框架
程序的主框架是一个while循环,每输入一个数据就处理一次,直到人为结束程序或输入
非法数据而终止输入。代码如下:
while True: # 循环输入
n = int(input())
guess(n) # 调用函数验证哥德巴赫猜想(2)使用函数判断n是否为素数
在算法设计中我们详细介绍了fun()函数,它的功能就是判断传进来的形参n是否为素数,
其代码如下:
# 判断是否为素数
def fun(n):
if n == 2:
return 1 # n是2,返回1
if n % 2 == 0:
return 0 # n是偶数,不是素数,返回0
i = 3
while i <= math.sqrt(n):
if n % i == 0:
return 0 # n是奇数,不是素数,返回0
i += 2
return 1 (3)使用函数验证哥德巴赫猜想
在算法设计中,我们介绍了guess()函数,它的功能就是验证传入的参数n是否满足哥德巴
赫猜想,其代码如下:
# 验证哥德巴赫猜想
def guess(n):
ok = 0 # 进入循环前先置标志位
i = 2
while i <= (n // 2):
if fun(i):
if fun(n - i):
print("%d %d\n" % (i, n - i)) # i和n-i都是素数,则打印
ok = 1
if i != 2:
i += 1
if ok:
break # 已打印出所需要的输出结果,跳出循环
i += 1程序的流程图如图5.3所示。
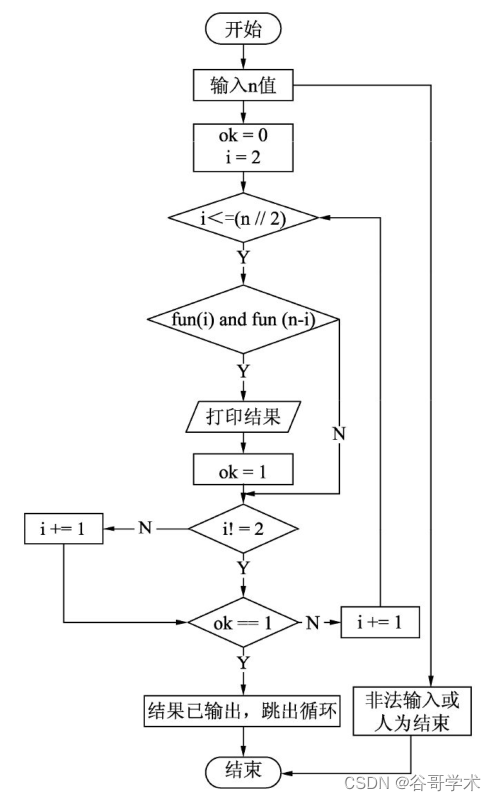
5.完整的程序
根据上面的分析,编写程序如下:
#!/usr/bin/python3
# -*- coding: utf-8 -*-
# @author : liuhefei
# @desc: 哥德巴赫猜想
import math
# 判断是否为素数
def fun(n):
if n == 2:
return 1 # n是2,返回1
if n % 2 == 0:
return 0 # n是偶数,不是素数,返回0
i = 3
while i <= math.sqrt(n):
if n % i == 0:
return 0 # n是奇数,不是素数,返回0
i += 2
return 1 # n是除2以外的素数,返回1
# 验证哥德巴赫猜想
def guess(n):
ok = 0 # 进入循环前先置标志位
i = 2
while i <= (n // 2):
if fun(i):
if fun(n - i):
print("%d %d\n" % (i, n - i)) # i和n-i都是素数,则打印
ok = 1
if i != 2:
i += 1
if ok == 1:
break # 已打印出所需要的输出结果,跳出循环
i += 1
if __name__ == "__main__":
while True: # 循环输入
n = int(input())
guess(n) # 调用函数验证哥德巴赫猜想 6.运行结果
在PyCharm下运行程序,分别输入4、6、8、10、12,每输入一个数据后,按Enter键则立
即打印出该数据的结果,如图5.4所示。

7.问题拓展
在该问题中我们定义了fun()函数来判断数n是否为素数,在fun()函数中,针对n的奇偶性
进行了不同的处理,只要n是偶数,则肯定不是素数,这样就只需对n是奇数的情况进行判
断,如下面的代码中加粗部分所示:
# 判断是否为素数
def fun(n):
if n == 2:
return 1 # n是2,返回1
if n % 2 == 0:
return 0 # n是偶数,不是素数,返回0
i = 3
while i <= math.sqrt(n):
if n % i == 0:
return 0 # n是奇数,不是素数,返回0
i += 2
return 1 如果n是奇数,则n包含的因子也只能为奇数,否则n就应该是偶数,因此循环变量i每次
自增2,且i的变化范围为 。使用这种方式来判断素数,与从 逐个比较相比,进一
步缩小了比较范围,处理速度也进一步获得了提高