博弈类人工智能，其中一个方法就是：博弈树极大极小值alpha-beta剪枝搜索。

是不是觉得这个名字很牛逼， 但经过我的详细解读， 你马上就会发现，原来不过如此。

对于要实现一个会智能下五子棋的AI，要怎么去实现呢？自然想到的方法就是，让计算机把每一步的可能性都试一遍，看走在那效果最好。 其实就是搜索的方法，搜索所有的下一步可能性，择优选择。这就是博弈树搜索。

博弈树搜索

什么是博弈树搜素呢？博弈就是相互采取最优策略斗争的意思。比如说下五子棋，你下一步，我下一步，这就是相互博弈。假设棋盘的大小是10*10,那就是100个点可以下， 那么第一步可选择的可能就是100， 假设是下在了A点， 那么第二步就有除了A点的剩下的99个点的可能。 假设下在了B点， 那么第二步就有除了B点的剩下的99个点的可能，假设下在了C点…

看到没有， 我上面的假设可以复制100次， 同时基于其中的一个点，第二步又可以复制99次， 以此类推，就构成了一个树状的结构：

好了， 问题来了， 这么多可能性， 走哪一步才是最优的呢？ 这就是下一步，极大极小值搜索。

极大极小值搜索

对于一个棋局， 判断它对我来说是占优势还是劣势， 能不能用个比较确定的数值来评估呢？答案是可以的。 对于五子棋就是统计目前的棋型，并累加分数。 比如如果有4个子连起来了， 那就给个很高的评分，因为下一步就可以赢了， 如果是3个子连起来了，给个相对较低的评分，因为不一定就能赢，对方会堵你呢， 但是比只有2 个子连在一起的得分要高吧， 如是就有了下面的棋型评分表：

# 棋型的评估分数
shape_score = [(50, (0, 1, 1, 0, 0)),(50, (0, 0, 1, 1, 0)),(200, (1, 1, 0, 1, 0)),(500, (0, 0, 1, 1, 1)),(500, (1, 1, 1, 0, 0)),(5000, (0, 1, 1, 1, 0)),(5000, (0, 1, 0, 1, 1, 0)),(5000, (0, 1, 1, 0, 1, 0)),(5000, (1, 1, 1, 0, 1)),(5000, (1, 1, 0, 1, 1)),(5000, (1, 0, 1, 1, 1)),(5000, (1, 1, 1, 1, 0)),(5000, (0, 1, 1, 1, 1)),(50000, (0, 1, 1, 1, 1, 0)),(99999999, (1, 1, 1, 1, 1))]

这篇文章的示例是用python代码实现， 上面是我列出的一些常见的五子棋形状，1代表有子落在此处，0代表是空位，下一步可以下在此处。 前面是对应的分值。

那么对应评估局面上的分数， 就是统计所有匹配的棋型得分并累加。这个分数的统计就叫做评估函数，而这个评估函数的好坏是非常重要的， 下面的算法都是固定的，任何博弈类游戏都适合， 但评估函数就千差万别了。

# 评估函数
def evaluation(is_ai):total_score = 0if is_ai:my_list = list1enemy_list = list2else:my_list = list2enemy_list = list1# 算自己的得分score_all_arr = []  # 得分形状的位置 用于计算如果有相交 得分翻倍my_score = 0for pt in my_list:m = pt[0]n = pt[1]my_score += cal_score(m, n, 0, 1, enemy_list, my_list, score_all_arr)my_score += cal_score(m, n, 1, 0, enemy_list, my_list, score_all_arr)my_score += cal_score(m, n, 1, 1, enemy_list, my_list, score_all_arr)my_score += cal_score(m, n, -1, 1, enemy_list, my_list, score_all_arr)#  算敌人的得分， 并减去score_all_arr_enemy = []enemy_score = 0for pt in enemy_list:m = pt[0]n = pt[1]enemy_score += cal_score(m, n, 0, 1, my_list, enemy_list, score_all_arr_enemy)enemy_score += cal_score(m, n, 1, 0, my_list, enemy_list, score_all_arr_enemy)enemy_score += cal_score(m, n, 1, 1, my_list, enemy_list, score_all_arr_enemy)enemy_score += cal_score(m, n, -1, 1, my_list, enemy_list, score_all_arr_enemy)total_score = my_score - enemy_score*ratio*0.1return total_score

对于AI要走在那里最好，那就是计算它在走在某一个点后， 计算局面的得分，然后取得分最大的那个点，不就是最应该下的点吗？ so easy！ 这就是极大值搜索。

但不要忘了， 你这是只考虑了一步啊， 搜索的深度只有1， 没听说老谋深算的家伙都是考虑3步的吗， 也就是要考虑下了这一步后，对手下一步会怎么下。对手不傻，肯定会在我得分最小的那个点上下， 这个得分是相对于我而言的，我的得分最小， 那就是对手的最优策略了， 这就是极小值搜索。

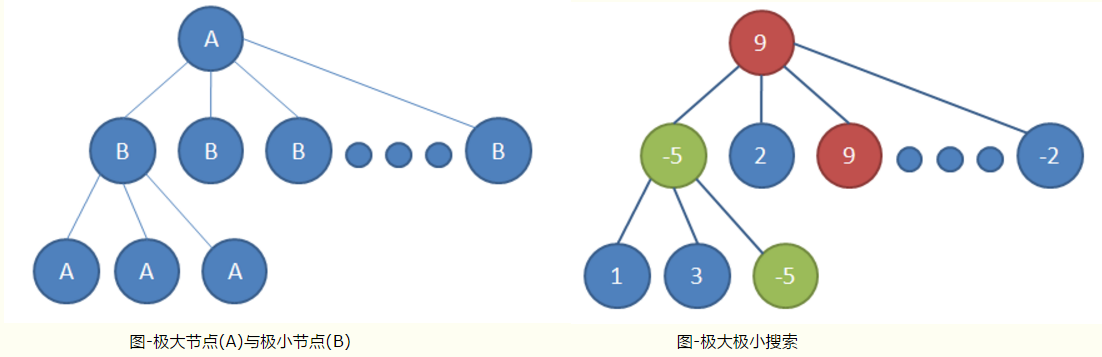
AI要考虑3步的话， 那就是搜索深度为3，那就是搜索落在那个点，3步后得分最大。这就可以和看能看3步棋的老家伙对抗了。

关于极大极小值的伪代码(注意是伪代码，不是本文的示例的python代码)：
这里面有递归，相信能很好理解吧。

int MinMax(int depth) { // 函数的评估都是以白方的角度来评估的if (SideToMove() == WHITE) {　// 白方是“最大”者 return Max(depth); } else {　　　　　　　　　　　// 黑方是“最小”者 return Min(depth); } 
} 　 
int Max(int depth) { int best = -INFINITY; if (depth <= 0) { return Evaluate(); } GenerateLegalMoves(); while (MovesLeft()) { MakeNextMove(); val = Min(depth - 1); UnmakeMove(); if (val > best) { best = val; } } return best; 
} 　 
int Min(int depth) { int best = INFINITY;　// 注意这里不同于“最大”算法 if (depth <= 0) { return Evaluate(); } GenerateLegalMoves(); while (MovesLeft()) { MakeNextMove(); val = Max(depth - 1); UnmakeMove(); if (val < best) { 　// 注意这里不同于“最大”算法 best = val; } } return best; 
} 

到这里， 感觉不就完了吗？可以和老家伙一决高下了？ 这就错了， 忽略了一个很重要的问题， 就是搜索的计算量， 你以为计算机是机器，cpu是 intel i7就瞬间完成计算啊， 这个博弈树，之所以叫树，那么他的枝点的数量，是以指数增长的，搜索深度3和搜索深度5那计算量差的可不是几倍的概念。而是差指数倍的概念。 所以虽然五子棋棋盘没围棋大， 但是按照这种全部可能性都搜索的方法去搜索，是要死电脑的。

于是，聪明的人对其进行了优化， 这就是alpha-beta剪枝搜索。

alpha-beta剪枝搜索

假设博弈树的搜索情况如下图：

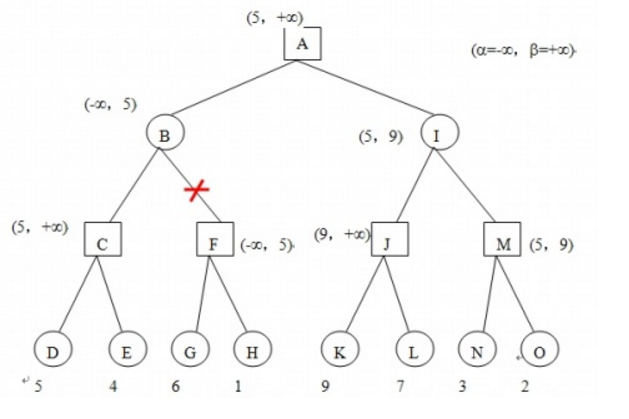
α为已知的最大值， β为已知的最小值， 因为还没搜索不知道是多少，保险起见，初始化为-∞ 和+∞。

搜索到D的时候，局面得分是5，（顺便说一句，这样的搜索是深度优先搜索，什么是深度优先搜索，可百度）那么也就是说要搜索最大值，那么只可能会在（5，+∞） 之间， 同理，要搜索最小值，也只会在（-∞，5）之间。
继续搜索， 搜索到G时，F暂时等于6 ，F是要找最大值， 那么F不可能再小于6了， 而B是要找最小值的，B的已知最小值是在（-∞，5）之间的， 你F还不可能比6小了， 我还要搜索你F后面的情况干嘛？不是浪费时间吗， 于是果断咔嚓掉F这个分支，不搜索了， 这就是剪枝。
同样对于另外一边的已知可能的极限范围β也是一样的情况，遇到就算是搜索也是浪费时间的情况，就剪枝不搜索了。
这样就减少了很多不必要是搜索步骤， 特别是一开始就找到最有可能的极大极小值， 更能迅速的剪枝。 怎么一开始尽快的找到可能的极大极小值呢， 后面再说。 先插播一下，负值极大法。

负值极大法

上面的伪代码有求极大值， 极小值， 还要两个函数， 其实都求各自的最大值， 这个各自的最大值是值， 都站在自己的一方来求最大值， 对手的最大值前面加个负号，不就是对我来说的最小值吗? 有点绕， 但道理相信很容易理解， 这样的好处就是把求最大最小值写在一个函数里了， 看代码：

# 负值极大算法搜索 alpha + beta剪枝
def negamax(is_ai, depth, alpha, beta):# 游戏是否结束 | | 探索的递归深度是否到边界if game_win(list1) or game_win(list2) or depth == 0:return evaluation(is_ai)blank_list = list(set(list_all).difference(set(list3)))order(blank_list)   # 搜索顺序排序  提高剪枝效率# 遍历每一个候选步for next_step in blank_list:global search_countsearch_count += 1# 如果要评估的位置没有相邻的子， 则不去评估  减少计算if not has_neightnor(next_step):continueif is_ai:list1.append(next_step)else:list2.append(next_step)list3.append(next_step)value = -negamax(not is_ai, depth - 1, -beta, -alpha)if is_ai:list1.remove(next_step)else:list2.remove(next_step)list3.remove(next_step)if value > alpha:print(str(value) + "alpha:" + str(alpha) + "beta:" + str(beta))print(list3)if depth == DEPTH:next_point[0] = next_step[0]next_point[1] = next_step[1]# alpha + beta剪枝点if value >= beta:global cut_countcut_count += 1return betaalpha = valuereturn alpha

此处实际的代码可能不太好理解，上伪代码应该好看些，如下：

int negamax(GameState S, int depth, int alpha, int beta) {// 游戏是否结束 || 探索的递归深度是否到边界if ( gameover(S) || depth == 0 ) {return evaluation(S);}// 遍历每一个候选步foreach ( move in candidate list ) {S' = makemove(S);value = -negamax(S', depth - 1, -beta, -alpha);unmakemove(S') if ( value > alpha ) {// alpha + beta剪枝点if ( value >= beta ) {return beta;}alpha = value;}}return alpha;
}

其他优化

好了， 到这里基本告一段落了， 但针对五子棋的特点， 可以加一些其他优化， 如搜索的开始点， 从上一步的点的周围搜索起，能尽快的找到相对较大的极大值， 和相对较小的极小值，从而更快的剪枝。 因为邻近的点是最有可能的。 另外为了减少计算量， 我还把 四面八方都没有相邻的子的位置给去掉了， 因为这样的位置不大可能是有价值的位置， 当然这个优化不严谨， 但为了减少计算量。。