1. 引言

我们上次介绍了利用到了baseline的一种算法：REINFORCE。现在我们来学习一下另一种利用到baseline的算法：Advantage Actor-Critic(A2C)

2. 数学推导

我们在Sarsa算法中推导出了这个公式 $Q_{\pi}(s_t,a_t)=E_{S_{t+1},A_{t+1}}[R_t+\gamma Q_{\pi}(S_{t+1},A_{t+1})]$ ，我们分部期望 $Q_{\pi}(s_t,a_t)=E_{S_{t+1}}[E_{A_{t+1}}[R_t+\gamma Q_{\pi}(S_{t+1},A_{t+1})]]=E_{S_{t+1}}[R_t+\gamma V_{\pi}(S_{t+1})]$

两边对 $A_t$ 求期望 $V_{\pi}(s_{t})=E_{A_t}[E_{S_{t+1}}[R_t+\gamma V_{\pi}(S_{t+1})]]=E_{A_t,S_{t+1}}[R_t+\gamma V_{\pi}(S_{t+1})]$

我们便得到了关于状态价值函数的递推关系式 $V_{\pi}(s_{t})=E_{A_t,S_{t+1}}[R_t+\gamma V_{\pi}(S_{t+1})]$

使用蒙特卡罗算法近似右侧期望 $r_t+\gamma V_{\pi}(s_{t+1})\approx E_{A_t,S_{t+1}}[R_t+\gamma V_{\pi}(S_{t+1})]$ ，我们得到

$V_{\pi}(s_t)\approx r_t+\gamma V_{\pi}(s_{t+1})$ 又由 $Q_{\pi}(s_t,a_t)=E_{S_{t+1}}[R_t+\gamma V_{\pi}(S_{t+1})]$ ，也是使用蒙特卡罗算法，我们得到 $Q_{\pi}(s_t,a_t)\approx r_t+\gamma V_{\pi}(s_{t+1})$ ，总结一下，现在我们得到两个近似公式，分别记为公式1和公式2。

$Q_{\pi}(s_t,a_t)\approx r_t+\gamma V_{\pi}(s_{t+1})$
$V_{\pi}(s_t)\approx r_t+\gamma V_{\pi}(s_{t+1})$

它们在后面各有用处。

在REINRORCE中我们推导出了随机梯度的表达式 $g(a_t)=\frac{\partial \,\ln{\pi}(a_t|s_t;\theta)}{\partial \,\theta}(Q_{\pi}(s_t,a_t)- V_{\pi}(s_t))$ 我们用它来更新策略函数，这里的 $Q_{\pi}(s_t,a_t)- V_{\pi}(s_t)$ 就是我们之前在Dueling Network讲过的优势函数，这便是Advantage的来源。现在需要解决 $Q_{\pi}(s_t,a_t)$ 和 $V_{\pi}(s_t)$ 两个未知量的近似，由公式1，我们解决了 $Q_{\pi}(s_t,a_t)$ 的近似问题，对于 $V_{\pi}(s_t)$ 我们使用神经网络 $v(s;w)$ 来近似它，于是我们得到

$g(a_t)\approx \frac{\partial \,\ln{\pi}(a_t|s_t;\theta)}{\partial \,\theta}(r_t+\gamma v(s_{t+1};w)- v(s_t;w))$ ，由于 $r_t+\gamma v(s_{t+1;w})$ 含有更多的真实信息，我们将其作为TD target 使 $v(s_t;w)\rightarrow r_t+\gamma v(s_{t+1};w)$ 来优化价值函数的参数。

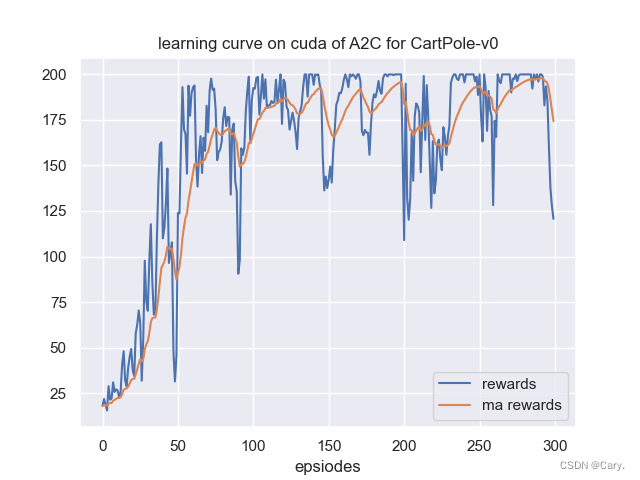
3. 算法

A2C算法本质上还是一种Actor-Critic方法，所以还是分为两个神经网络进行训练，一个是策略网络(Actor)，另一个是价值网络(Critic)

观测到一个transition $(s_t,a_t,r_t,s_{t+1})$
计算TD target $y_t=r_t+\gamma v(s_{t+1};w)$
计算TD error $\delta_t=v(s_t;w)-y_t$
通过梯度上升 $\theta\leftarrow \theta-\beta\,\delta_t\frac{\partial \,\ln{\pi}(a_t|s_t;\theta)}{\partial \,\theta}$ 更新策略网络
通过梯度下降 $w\leftarrow w-\alpha\delta_t\,\frac{\partial \,v(s_t;w)}{\partial \,w}$ 更新价值网络