问题重述

一个慢跑者在平面上按如下规律跑步: X=10+20cost， Y=20+15sint。突然有一只狗攻击他，这只狗从原点出发，以恒定速率跑向慢跑者，狗的运动方向始终指向慢跑者。分别研究w=20,w=5时狗是否能追上慢跑者；如果能追上，求所用的时间，画出狗与慢跑者之间距离的变化曲线。

问题分析

本文将问题看作追及问题，根据狗与人的位置关系建立微分方程。由于狗从原点出发以恒定速率跑向慢跑者并且狗的运动方向始终指向慢跑者，故问题可以看作狗与人始终在同一直线段的追及问题。

假设时刻t时，人的坐标为(X(t),Y(t)),狗的坐标(x(t),y(t))。分解狗的速度，此时有：

由于狗从原点出发以恒定速率跑向慢跑者并且狗的运动方向始终指向慢跑者，因此可以将问题看作狗在x，y两个方向上对人的追及问题。分别建立狗x，y关于t的方程，可得微分方程组：

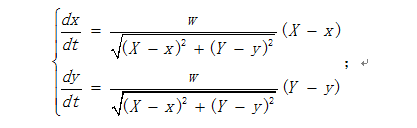
最后将已知条件带入方程组可得狗的运动轨迹方程：

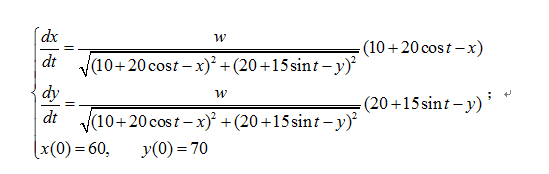
求解结果

通过计算结果可以知道，当w=20时狗能追上慢跑者，而w=5时并不能追上慢跑者。当w=20时，求解出t=4.188时狗正好能追上慢跑者，此时的轨迹图为：