目录
题目描述
输入
输出
样例
输入数据 1
输出数据 1
提示
数据规模与约定
----------------------------------------------------------------------------------------------
分析
Code
题目描述
有 n个容量无穷大的水壶,它们从 1∼n 编号,初始时 i 号水壶中装有 Ai 单位的水。
你可以进行不超过 k次操作,每次操作需要选择一个满足 1≤x≤n−1 的编号 x,然后把 x 号水壶中的水全部倒入 x+1 号水壶中。
最后你可以任意选择恰好一个水壶,并喝掉水壶中所有的水。现在请你求出,你最多能喝到多少单位的水。
输入
第一行一个正整数 n,表示水壶的个数。
第二行一个非负整数 k,表示操作次数上限。
第三行 n 个非负整数,相邻两个数用空格隔开,表示水壶的初始装水量 A1,A2, ⋯, An。
输出
一行,仅一个非负整数,表示答案。
样例
输入数据 1
10
5
890 965 256 419 296 987 45 676 976 742输出数据 1
3813提示
数据规模与约定
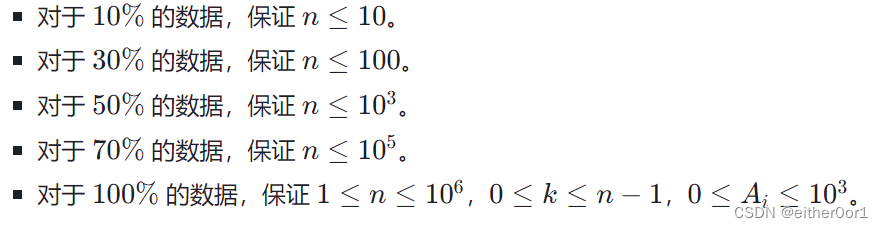
----------------------------------------------------------------------------------------------
分析
【把 x 号水壶中的水全部倒入 x+1 号水壶中。这样k次操作,你最多能喝到多少单位的水。】关键点是这句话,将x倒入到x+1,实际就是前缀和,将前一个累加到后一个,要想喝最多水,k次操作都必须是连续区间操作才行,这样就转换为区间长度为K的前缀和,为了求区间长度和,实际就是求区间前缀和差分。
例如 :A1,A2,...,A8
假设K=5
前缀和为Sn
S0=A0
S1=S0+A1
S2=S1+A2
...
S8=S7+A8
那么每连续5个区间的累加和计算如下: (用Sub[]存储)
Sub[1]=S[5]-S[0]=A5+A4+A3+A2+A1
Sub[2]=S[6]-S[1]=A6+A5+A4+A3+A2
Sub[3]=S[7]-S[2]=A7+A6+A5+A4+A3
Sub[4]=S[8]-S[3]=A8+A7+A6+A5+A4
最后只要求Sub[]的最大值就大功告成。
Code
#include<bits/stdc++.h>
using namespace std;
long long n,k,s[1000100],ans;
int main()
{cin >> n >> k;for(int i = 1,x;i <= n;++i){cin >> x;s[i] = s[i - 1] + x;}for(int i = 1;i <= n-k;i++){//枚举区间 ans = max(ans,s[i+k] - s[i-1]);//求最值 }cout << ans << endl;return 0;
}