239. 滑动窗口最大值 || 剑指 Offer 59 - I. 滑动窗口的最大值 ●●●

描述

给定一个数组 nums 和滑动窗口的大小 k，请找出所有滑动窗口里的最大值。

示例

输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7]

	  滑动窗口的位置                最大值-------------------------     -----[1  3  -1] -3  5  3  6  7       31 [3  -1  -3] 5  3  6  7       31  3 [-1  -3  5] 3  6  7       51  3  -1 [-3  5  3] 6  7       51  3  -1  -3 [5  3  6] 7       61  3  -1  -3  5 [3  6  7]      7

题解

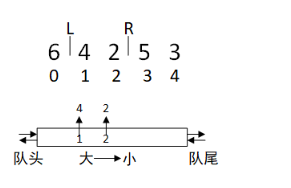
1. 双端队列 构造 单调队列

随着窗口的移动，队列也一进一出，每次移动之后，队列告诉我们里面的最大值是什么。

队列没有必要维护窗口里的所有元素，只需要维护有可能成为窗口里最大值的元素就可以了，同时保证队里里的元素数值是由大到小的。

那么这个维护元素单调递减的队列就叫做单调队列，即单调递减或单调递增的队列。

因此，每次移动窗口时，对队列进行必要的移除操作，来保持进入窗口的数值加入队列后仍是一个单调队列，最后取队列首即为当前窗口最大值。

• 时间复杂度：$O(n)$，其中 n 是数组 nums 的长度。每一个下标恰好被放入队列一次，并且最多被弹出队列一次，因此时间复杂度为 O(n)。
• 空间复杂度：$O(k)$。使用的数据结构是双向的，因此「不断从队首弹出元素」保证了队列中最多不会有超过 k+1 个元素，因此队列使用的空间为 O(k)。

class Solution {
public:vector<int> maxSlidingWindow(vector<int>& nums, int k) {int n = nums.size();vector<int> ans;deque<int> que;                     // 双端队列for(int i = 0; i < k; ++i){         // 前k个数字进行处理，形成单调队列while(!que.empty() && nums[i] > que.back()){que.pop_back();}que.push_back(nums[i]);}ans.emplace_back(que.front());for(int i = k; i < n; ++i){         // 移动窗口，保持单调队列if(nums[i-k] == que.front()) que.pop_front();   // 如果移出窗口的数字还在队列中，那么他只能是队列首，应pop，否则不操作while(!que.empty() && nums[i] > que.back()){    que.pop_back();                             // 通过移除更小数字来保持单调，将进入窗口的数字加入队列}que.push_back(nums[i]);ans.emplace_back(que.front());  // 取队列首，数值最大}return ans;}
};