邻域均值

邻域均值

• 题意比较好理解，就是算一些数字。
• 如果采用暴力方法的话，就是用一个边长为 $2\ast r+1$ 的正方形框框住大矩阵，然后遍历这个框，求出其平均值，然后移动正方形框，直到大矩阵内所有像素点都被遍历到为止。
• 不过粗略计算其复杂度 $600\ast 600\ast 100\ast 100=3,600,000,000$，显然会超时。
• 所以此题的关键在于优化，没必要每次移动了正方形框后都去重新计算正方形框内的所有值之和，有时候（在一行或一列内移动时）正方形框在移动前后两个状态的值只相差一行或一列，这有点像滑动窗口了，移动后减去失去的那一行或列，并加上新覆盖的一行或列，这样每一次移动只需要计算一维的量，而不再是计算整个正方形框的二维的量了，这时候复杂度直接少了两个0，是$36,000,000$，显然，$10^7$ 的复杂度是能通过此题的。
• 细节：计算这种题，肯定是要在原始矩阵的周围增添若干0行的，以达到正方形框的统一性，防止在矩阵的角和边进行特殊计算，增加代码的复杂度。但是这样的话就会产生另一个难题，我增添了几行0，显然正方形框内的和很容易算，那么占了多少个原始矩阵的像素点呢？这是本题一个恶心人的地方，要计算的东西和原矩阵的像素点个数有关，而不是单纯地计算和。
• 那么就需要继续探索某一个像素点坐标和正方形框边长参数 $r$ 的关系了。显然，如果告诉我某一个像素点的坐标 $(x,y)$ 和参数 $r$，我就可以计算出以这个像素点为中心的正方形框里面有多少个原矩阵的像素点的话，那么本题就可以算解决了。
• 实际是可以找出来这个关系的。
  
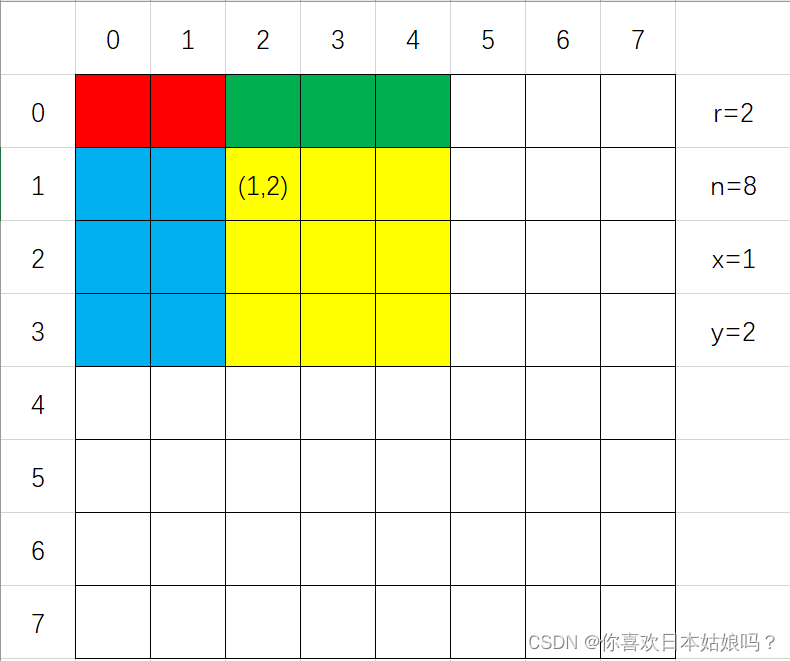
• 假设现在正方形框的中心为像素点 $(1,2)$，那么图中彩色部分表示原始矩阵中的像素点，之所以染成4种颜色，是因为像素点个数与坐标和 $r$ 的关系表达式可以分成4个部分。
• 下面直接给出公式的具体样子，具体推导应该是一目了然的，这里就不推导了。
  • 黄色部分：$(min(r,n-x-1)+1)\ast (min(r,n-y-1)+1)$
  • 绿色部分：$min(r,x)\ast (min(r,n-y-1)+1)$
  • 蓝色部分：$min(r,y)\ast (min(r,n-x-1)+1)$
  • 红色部分：$min(r,x)\ast min(r,y)$
• 注意这里的 $x$ 和 $y$ 是行号和列号，而不是什么直角坐标系里面的横纵坐标。
• 有了上述的关系式，那么此题基本算是解决了。
• 下面直接给出代码

代码如下

#include <iostream>
#include <vector>
using namespace std;void solve() {int n = 0, L = 0, r = 0, t = 0;  // 题目变量scanf("%d%d%d%d", &n, &L, &r, &t);// 在原矩阵周围添加冗余的r行0vector<vector<int>> a(2 * r + n, vector<int>(2 * r + n, 0));// 用于存储所有的正方形框里的和vector<vector<int>> sums(n, vector<int>(n, 0));// 读入，注意起始位置for (int i = r; i < r + n; i++) {for (int j = r; j < r + n; j++) {scanf("%d", &a[i][j]);}}// 先计算出第一个正方形框的和，后续才好移动for (int i = 0; i < 2 * r + 1; i++) {for (int j = 0; j < 2 * r + 1; j++) {sums[0][0] += a[i][j];}}// 先向下移动，为每一行开个头，之后再对每一行进行移动for (int i = r + 1; i < r + n; i++) {sums[i - r][0] =sums[i - r - 1][0];  // 这一行格子的初值是上一行对应格子的值for (int j = 0; j < 2 * r + 1; j++) {sums[i - r][0] -= a[i - r - 1][j];  // 减去离开的那一行sums[i - r][0] += a[i + r][j];      // 加上新覆盖的那一行}}// 对每一行进行移动// 当然也可以把上面的代码合在这里面，不过那样代码很难看，何必呢。for (int i = 0; i < n; i++) {for (int j = r + 1; j < n + r; j++) {sums[i][j - r] = sums[i][j - r - 1];for (int k = 0; k < 2 * r + 1; k++) {sums[i][j - r] -= a[i + k][j - r - 1];sums[i][j - r] += a[i + k][j + r];}}}// 定义存储答案的变量和一个临时变量int ans = 0, tt = 0;// 遍历"和矩阵"，计算区域个数for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {// 计算像素点个数tt = (min(r, n - i - 1) + 1) * (min(r, n - j - 1) + 1) +min(r, i) * (min(r, n - j - 1) + 1) +min(r, j) * (min(r, n - i - 1) + 1) + min(r, i) * min(r, j);// 知道了像素点个数后，也不是用和去除以像素点个数来计算平均值，而是使用乘法来判断// 符合题意就加入答案ans += (tt * t >= sums[i][j]);}}// 输出即可printf("%d\n", ans);
}int main(void) {// freopen("in.txt", "r", stdin);// freopen("out.txt", "w", stdout);solve();// fclose(stdin);// fclose(stdout);return 0;
}