二分图整理

news/2024/12/29 1:36:48/

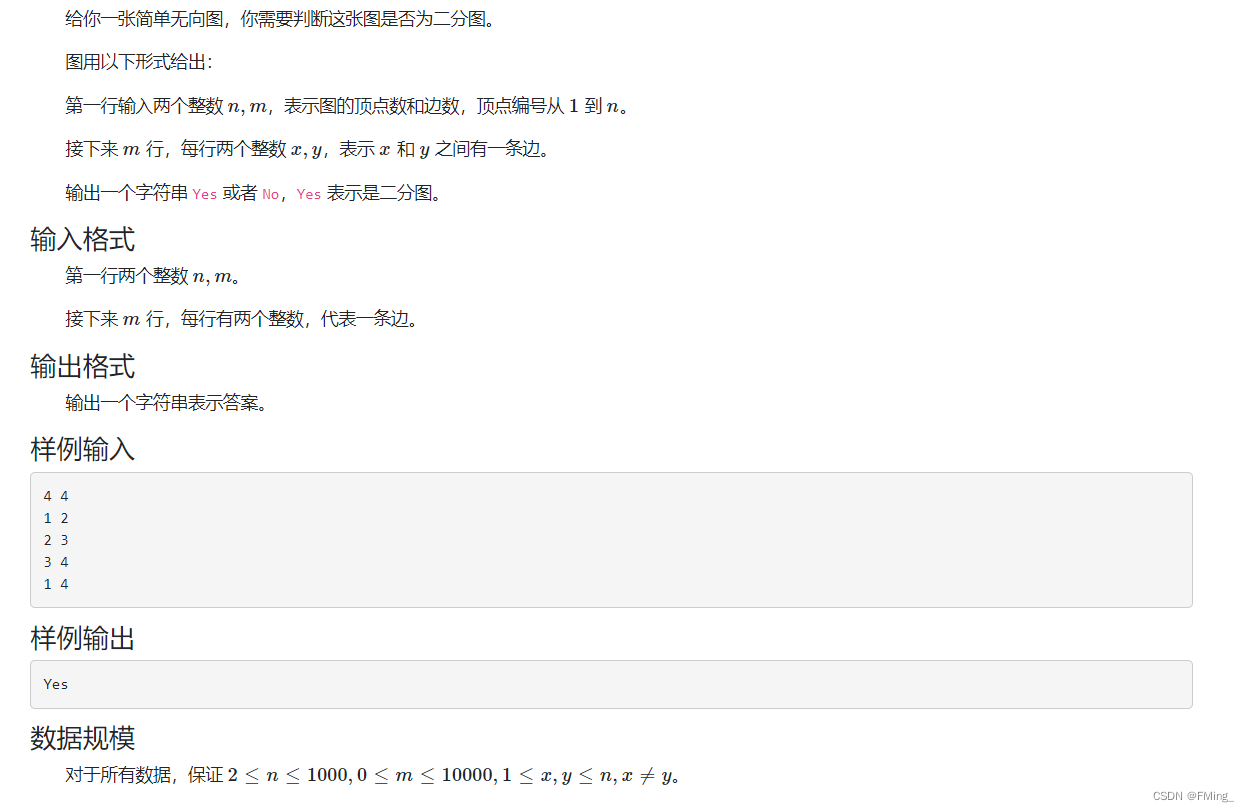
 定义：如果一张图的n个节点可以分成A,B两个不相交的非空集合，并且同一集合内的点之间没有边相连，那么称该无向图为二分图。

定理：二分图中不存在长度为奇数的环；就比如这样的就不是二分图

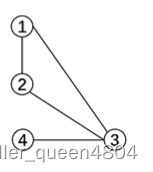
这一发现无论怎么分，总会有一个集合的点之间是有边的；

判断一个图是否是二分图可以用黑白染色法来处理，当一个点被标记成黑色，那么与他相连的边都要是白色，如果有冲突了说明不是二分图；

匈牙利算法求二分图最大匹配

P3386 【模板】二分图最大匹配 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

以上面这个题目为准来讲，可以把题目中的n个点看成是n个男人，m个点是m个女人，然后去枚举n个男生，假设到了第i个男生A，先去看看他中意的第一个女生是否已经和别人配对了，如果没有就让这个男的A和这个女生配对，否则就要看与这个女生配对的男B是否可以让出这个女的来，如何能够让出呢？也就是看看这个男B可不可以和别的女生配对，如果可以就把原来的那个女生让给男A，如果让不出来就去看下一个男A中意的女的，如果都不行，那就return 0；

#include <bits/stdc++.h>
#define endl '\n'
using namespace std;
#define int long long
const int N = 1e6+100;
int head[100005],cnt;
struct Edge
{int next,to;
}e[100005];
void addedge(int from,int to)
{e[++cnt].to=to;e[cnt].next=head[from];head[from]=cnt;
}
int n,m,E,ans,vis[505],match[505],g[505][505];
bool dfs(int u)
{for(int i=head[u];i;i=e[i].next){int v = e[i].to;if(vis[v]) continue;//这一个女的已经被访问过了vis[v]=1;if(!match[v]||dfs(match[v]))//这个女的没有配对或者这个女的可以被让出来{match[v]=u;return 1;}}return 0;
}
signed main()
{//cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);cin>>n>>m>>E;memset(g,0,sizeof(g));memset(match,0,sizeof(match));for(int i=1;i<=E;i++){int u,v;cin>>u>>v;if(g[u][v]) continue;g[u][v]=1;addedge(u,v);}ans=0;for(int i=1;i<=n;i++){memset(vis,0,sizeof(vis));if(dfs(i)) ans++;}cout<<ans<<endl;system("pause");return 0;
}

dinic

自己设一个虚拟的源点和汇点，源点到每个男生的容量是1，男生到自己心仪的女生的边容量也是1，女生到汇点的容量是1，反向边都是0，然后跑一遍dinic最后的答案就是最大匹配，这样的复杂度是根号n*m,是比匈牙利要优的

#include <bits/stdc++.h>
#define int long long
#define lowbit(x) ((x)&(-x))
#define endl '\n'
using namespace std;
const int mod=1e9+7;
int qpow(int a,int b)
{int res=1;while(b){if(b&1) res=res*a%mod;a=a*a%mod;b>>=1;}return res;
}
int getinv(int x){return qpow(x,mod-2);}
int head[500005],cnt=1;
struct Edge
{int to,next,w;
}e[500005];
void addedge(int from,int to,int w)
{e[++cnt].to=to;e[cnt].next=head[from];e[cnt].w=w;head[from]=cnt;
}
int s,t,d[500005],cur[500005],vis[505][505];
int n,m,E;
bool bfs()
{memset(d,0,sizeof(d));queue<int>q;q.push(s);d[s]=1;while(!q.empty()){int u=q.front();q.pop();for(int i=head[u];i;i=e[i].next){int j=e[i].to;if(d[j]==0&&e[i].w){d[j]=d[u]+1;q.push(j);if(j==t) return 1;}}}return 0;
}
int dfs(int u,int mf)
{if(u==t) return mf;int sum=0;for(int i=cur[u];i;i=e[i].next){cur[u]=i;int j=e[i].to;if(d[j]==d[u]+1&&e[i].w){int f=dfs(j,min(mf,e[i].w));e[i].w-=f;e[i^1].w+=f;sum+=f;mf-=f;if(mf==0) break;}}if(sum==0) d[u]=0;return sum;
}
int dinic()
{int flow=0;while(bfs()){memcpy(cur,head,sizeof(head));flow+=dfs(s,1e18);}return flow;
}
signed main()
{// cin.tie(0);// cout.tie(0);// ios::sync_with_stdio(0);//freopen("in.txt", "r", stdin);cin>>n>>m>>E;s=1;t=n+m+2;memset(vis,0,sizeof(vis));for(int i=1;i<=E;i++){int u,v;cin>>u>>v;if(vis[u][v]) continue;vis[u][v]=1;u+=1;v=n+v+1;addedge(u,v,1);addedge(v,u,0);}for(int i=2;i<=n+1;i++){addedge(s,i,1);addedge(i,s,0);}for(int i=2;i<=m+1;i++){addedge(i+n,t,1);addedge(t,i+n,0);}int ans=dinic();cout<<ans<<endl;system("pause");return 0;
}

最大匹配例题

372. 棋盘覆盖 - AcWing题库

可以发现对于一个点来说如果周围的点都可以用的话可以有四种情况来放置骨牌，这就可以转化成该点和四周的点都连一条线然后将整个棋盘划分成两部分去求最大匹配，可以将期盼划分成奇数点和偶数点，这也很好想，因为一个点和四周的点的奇偶性不能相同才可以，连完边后跑一遍dinic就可以了

AcWing 372. 棋盘覆盖 (最大流) - AcWing

#include <bits/stdc++.h>
#define int long long
#define lowbit(x) ((x)&(-x))
#define endl '\n'
using namespace std;
const int mod=1e9+7;
int qpow(int a,int b)
{int res=1;while(b){if(b&1) res=res*a%mod;a=a*a%mod;b>>=1;}return res;
}
int getinv(int x){return qpow(x,mod-2);}
int dx[5]={0,0,1,-1},dy[5]={1,-1,0,0};
int head[100005],cnt=1;
struct Edge
{int to,next,w;
}e[100005];
void addedge(int from,int to,int w)
{e[++cnt].to=to;e[cnt].w=w;e[cnt].next=head[from];head[from]=cnt;
}
int s,tar;
int d[100005],cur[100005];
int n,t,vis[105][105];
bool bfs()
{memset(d,0,sizeof(d));queue<int>q;q.push(s);d[s]=1;while(!q.empty()){int u=q.front();q.pop();for(int i=head[u];i;i=e[i].next){int j=e[i].to;if(d[j]==0&&e[i].w){d[j]=d[u]+1;q.push(j);if(j==tar) return 1;}}}return 0;
}
int dfs(int u,int mf)
{if(u==tar) return mf;int sum=0;for(int i=cur[u];i;i=e[i].next){cur[u]=i;int j=e[i].to;if(d[j]==d[u]+1&&e[i].w){int f=dfs(j,min(mf,e[i].w));e[i].w-=f;e[i^1].w+=f;mf-=f;sum+=f;if(mf==0) break;}}if(sum==0) d[u]=0;return sum;
}
int dinic()
{int flow=0;while(bfs()){memcpy(cur,head,sizeof(head));flow+=dfs(s,1e18);}return flow;
}
int getnum(int x,int y)
{return (x-1)*n+y;
}
signed main()
{// cin.tie(0);// cout.tie(0);// ios::sync_with_stdio(0);//freopen("in.txt", "r", stdin);cin>>n>>t;s=0,tar=n*n+1;for(int i=1;i<=t;i++) {int u,v;cin>>u>>v;vis[u][v]=1;}for(int i=1;i<=n;i++)for(int j=1;j<=n;j++){if(!vis[i][j]){if((i+j)&1){for(int k=0;k<4;k++){int x=i+dx[k],y=j+dy[k];if(x>n||x<1||y>n||y<1||vis[x][y]) continue;addedge(getnum(i,j),getnum(x,y),1);addedge(getnum(x,y),getnum(i,j),0);}addedge(s,getnum(i,j),1);addedge(getnum(i,j),s,0);}else{addedge(getnum(i,j),tar,1);addedge(tar,getnum(i,j),0);}}}int ans=dinic();cout<<ans<<endl;system("pause");return 0;
}

P1129 [ZJOI2007] 矩阵游戏 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

这个题自己一点思路都没有，感觉看这种图论题越看脑子就越呆，啥也想不进去，，，

其实从第i行看，如果a[i][j]=1的话，那么这个1只会在第j行才会发挥作用，也就说明第i行可以移动到第j行去，我们给像第i行和第j列这样的行列都连一条边，可以发现如果最大匹配大于等于n的话就说明每一行都有相应的列可以换到这，那么跑一遍dinic去看看最大匹配是否大于等于n就可以了

题解 P1129 【[ZJOI2007]矩阵游戏】 - Aurora的博客 - 洛谷博客

#include <bits/stdc++.h>
#define int long long
#define lowbit(x) ((x)&(-x))
#define endl '\n'
using namespace std;
const int mod=1e9+7;
int qpow(int a,int b)
{int res=1;while(b){if(b&1) res=res*a%mod;a=a*a%mod;b>>=1;}return res;
}
int head[500005],cnt=1;
struct Edge
{int to,next,w;
}e[500005];
void addedge(int from,int to,int w)
{e[++cnt].w=w;e[cnt].to=to;e[cnt].next=head[from];head[from]=cnt;
}
int T,n,s,t;
int d[100005],cur[100005];
bool bfs()
{memset(d,0,sizeof(d));queue<int>q;q.push(s);d[s]=1;while(!q.empty()){int u=q.front();q.pop();for(int i=head[u];i;i=e[i].next){int j=e[i].to;if(d[j]==0&&e[i].w){d[j]=d[u]+1;q.push(j);if(j==t) return 1;}}}return 0;
}
int dfs(int u,int mf)
{if(u==t) return mf;int sum=0;for(int i=cur[u];i;i=e[i].next){cur[u]=i;int j=e[i].to;if(d[j]==d[u]+1&&e[i].w){int f=dfs(j,min(e[i].w,mf));e[i].w-=f;e[i^1].w+=f;sum+=f;mf-=f;if(mf==0) break;}}if(sum==0) d[u]=0;return sum;
}
int dinic()
{int flow=0;while(bfs()){memcpy(cur,head,sizeof(cur));flow+=dfs(s,1e18);}return flow;
}
signed main()
{// cin.tie(0);// cout.tie(0);// ios::sync_with_stdio(0);//freopen("in.txt", "r", stdin);cin>>T;while(T--){cin>>n;s=0;t=2*n+1;for(int i=1;i<=n;i++){addedge(s,i,1);addedge(i,s,0);addedge(i+n,t,1);addedge(t,i+n,0);}for(int i=1;i<=n;i++)for(int j=1;j<=n;j++){int x;cin>>x;if(x){addedge(i,j+n,1);addedge(j+n,i,0);}}int ans=dinic();if(ans>=n) cout<<"Yes\n";else cout<<"No\n";for(int i=1;i<=cnt;i++) e[i].next=e[i].to=e[i].w=0;for(int i=1;i<=2*n+10;i++) head[i]=0;}system("pause");return 0;
}

  二分图最大权完美匹配 

 这样的题目前提一般都是保证给出的边是一定有完美匹配的，然后再给每个匹配边赋上权值去求权值总和最大的匹配是多少，这个算法的O(n^4)勉强看懂了，但是O(n^3)的没有看懂，先暂且把板子留在这吧

 模板 - KM算法（O(n^3)）（二分图最大权完美匹配）_繁凡さん的博客-CSDN博客

//Data
const int N=500;
int n,m,e[N+7][N+7];//KM
int mb[N+7],vb[N+7],ka[N+7],kb[N+7],p[N+7],c[N+7];
void Bfs(int u){int a,v=0,vl=0,d;for(int i=1;i<=n;i++) p[i]=0,c[i]=inf;mb[v]=u;do {a=mb[v],d=inf,vb[v]=1;for(int b=1;b<=n;b++)if(!vb[b]){if(c[b]>ka[a]+kb[b]-e[a][b])c[b]=ka[a]+kb[b]-e[a][b],p[b]=v;if(c[b]<d) d=c[b],vl=b;}for(int b=0;b<=n;b++)if(vb[b]) ka[mb[b]]-=d,kb[b]+=d;else c[b]-=d;v=vl;} while(mb[v]);while(v) mb[v]=mb[p[v]],v=p[v];
}
ll KM(){for(int i=1;i<=n;i++) mb[i]=ka[i]=kb[i]=0;for(int a=1;a<=n;a++){for(int b=1;b<=n;b++) vb[b]=0;Bfs(a);}ll res=0;for(int b=1;b<=n;b++) res+=e[mb[b]][b];return res;
}//Main
int main(){n=ri,m=ri;for(int a=1;a<=n;a++)for(int b=1;b<=n;b++) e[a][b]=-inf;for(int i=1;i<=m;i++){int u=ri,v=ri,w=ri;e[u][v]=max(e[u][v],w);}printf("%lld\n",KM());for(int u=1;u<=n;u++) printf("%d ",mb[u]);puts("");return 0;
}

 

有很多知识是借鉴的这篇文章

二分图（概念、相关算法和题目应用）(全面整理)_阐上的博客-CSDN博客_二分图


http://www.ppmy.cn/news/853000.html

相关文章

二 分 图

二 分 图

什么是二分图: 简单来说&#xff0c;如果图中点可以被分为两组&#xff0c;并且使得所有边都跨越组的边界&#xff0c;则这就是一个二分图。准确地说&#xff1a;把一个图的顶点划分为两个不相交子集 &#xff0c;使得每一条边都分别连接两个集合中的顶点。如果存在这样的划分…
阅读更多...
二分图（仅二分图基础讲解）

二分图（仅二分图基础讲解）

闲的无聊来写个二分图的讲解吧。 读者可能会疑惑&#xff0c;二分图&#xff1f;什么叫做二分图&#xff0c;是由二分思想演变的图吗&#xff1f; 但是&#xff0c;二分图各位都见过&#xff0c;只是不知道它叫二分图。以下开始二分图的讲解 二分图&#xff1a; 大家小学肯…
阅读更多...
embedding和向量数据库(pinecone)

embedding和向量数据库(pinecone)

embedding和向量数据库(pinecone) 玩了这么久的gpt&#xff0c;大家多少都会发现使用过程中有一些尴尬的点&#xff1a; LLM的训练数据是有ddl的&#xff0c;无法获取到最新的一些信息 LLM不知道答案&#xff0c;开始放飞自我&#xff0c;出现hallucination 想应用化&#xff…
阅读更多...
Linux rpm命令详解

Linux rpm命令详解

rpm -aq|grep yum|xargs rpm -e --nodeps #卸载所有yum相关包 rpm常见命令参数 用法: rpm [选项...] -a&#xff1a;查询所有套件&#xff1b; -b<完成阶段><套件档>或-t <完成阶段><套件档>&#xff1a;设置包装套件的完成阶段&#xff0c;并…
阅读更多...
苹果开发者_苹果iOS14.2/iPadOS开发者预览版下载-苹果iOS14.2/iPadOS开发者预览版Beta4固件大全下载 v1.0...

苹果开发者_苹果iOS14.2/iPadOS开发者预览版下载-苹果iOS14.2/iPadOS开发者预览版Beta4固件大全下载 v1.0...

苹果开发者预览版是一款可以帮助你更新最新的苹果系统的软件&#xff0c;很多人用习惯了苹果系统感觉改不过来了&#xff0c;其实习惯这个事情&#xff0c;突然的转变对于很多人来说都会有点不习惯&#xff0c;在这里你可以自己更新一个苹果的最新系统&#xff0c;虽然这个系统…
阅读更多...
Mac 防还原系统(设置固件密码)

Mac 防还原系统(设置固件密码)

分享一个给Mac设备设置固件密码的方法&#xff0c;一起来看看具体步骤吧。 1.OS X用户可以在开机的时候按住Option键&#xff0c;进入Recovery HD。注意&#xff0c;Recovery HD是OS X系统自带的急救模式&#xff0c;主要用于重装系统与修复磁盘等操作&#xff0c;删除了会有…
阅读更多...
简单提取iOS13的ipsw固件的内置壁纸(或文件)

简单提取iOS13的ipsw固件的内置壁纸(或文件)

1.先百度下“TransMac”,下载并安装。 没看到官方网站&#xff0c;就点第一个下载就好了 2.在下载安装的同时&#xff0c;将下载的ipsw文件的后缀ipsw改成rar,然后进行解压&#xff0c;得到下面文件夹里的东西。 其中有3个后缀为dmg的文件&#xff0c;找到大小最大的那个&#…
阅读更多...
airpods版本号_苹果更新 AirPods Pro 固件

airpods版本号_苹果更新 AirPods Pro 固件

原标题&#xff1a;苹果更新 AirPods Pro 固件 今日凌晨&#xff0c;苹果为 AirPods Pro 进行了固件升级&#xff0c;版本号由之前的 2C54/2B588 更新至 2D15。对于此次固件更新的内容仍未知&#xff0c;但有部分 AirPods Pro 用户一直抱怨前一个固件版本 2C54/2B588 的主动降噪…
阅读更多...
最新文章

Copyright @ 2022~2023