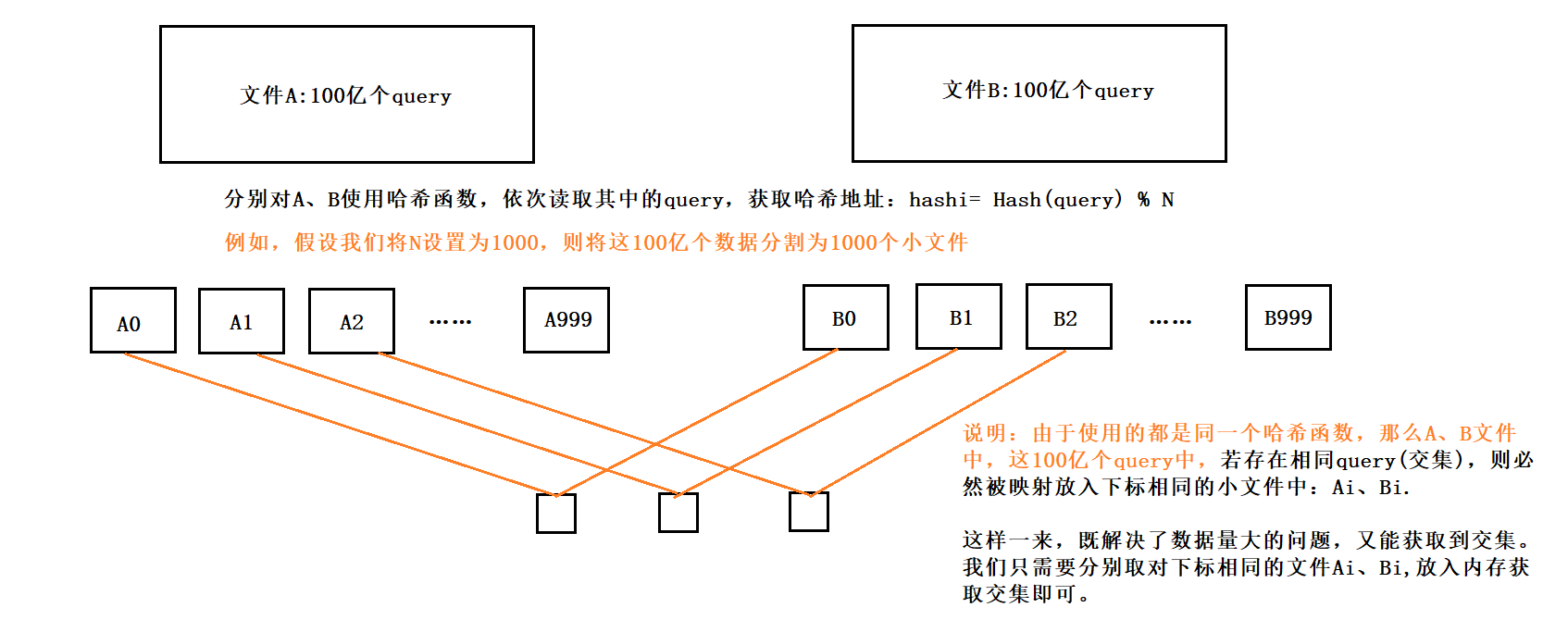
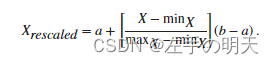🔗 运行环境:Matlab
🚩 撰写作者:左手の明天
🥇 精选专栏:《python》
🔥 推荐专栏:《算法研究》
#### 防伪水印——左手の明天 ####
💗 大家好🤗🤗🤗,我是左手の明天!好久不见💗
💗今天开启新的系列——重新定义matlab强大系列💗
📆 最近更新:2023 年 05 月 25 日,左手の明天的第 286 篇原创博客
📚 更新于专栏:matlab
#### 防伪水印——左手の明天 ####
🔥函数说明
N = normalize(A) 按向量返回 A 中数据的z值(中心为 0、标准差为 1)。
-
如果
A是向量,则normalize对整个向量A进行运算。 -
如果
A是矩阵,则normalize分别对A的每列进行运算。 -
如果
A是多维数组,则normalize沿A的大小不等于 1 的第一个维度进行运算。 -
如果
A是表或时间表,则normalize分别对A的每个变量进行运算。
N = normalize(A,dim) 指定要沿其进行运算的 A 的维度。例如,normalize(A,2) 对每个行进行归一化。
N = normalize(___,method) 使用上述任一语法指定归一化方法。例如,normalize(A,'norm') 通过欧几里德范数(2-范数)对 A 中的数据进行归一化。
N = normalize(___,method,methodtype) 指定给定方法的归一化类型。例如,normalize(A,'norm',Inf) 使用无穷范数归一化 A 中的数据。
method— 归一化方法归一化方法,指定为下列选项之一:
方法
描述
'zscore'均值为 0、标准差为 1 的 z值。
'norm'2-范数。
'scale'按标准差缩放。
'range'将数据范围重新缩放至 [0,1]。
'center'对数据进行中心化以使其均值为 0。
'medianiqr'中心化和缩放数据,使中位数为 0 且四分位差为 1。 要返回函数用于归一化数据的形参,请指定 C 和 S 输出实参。
methodtype— 方法类型方法类型,指定为数组、表、二元素行向量或类型名称,具体取决于指定的方法:
方法
方法类型选项
描述
'zscore'
'std'(默认值)中心化并缩放,使之均值为 0,标准差为 1。
'robust'中心化并缩放,使之中位数为 0,中位数绝对偏差为 1。
'norm'正数值标量(默认值为 2)
p-范数
Inf无穷范数。
'scale'
'std'(默认值)按标准差缩放。
'mad'按中位数绝对偏差缩放。
'first'按数据的第一个元素进行缩放。
'iqr'按四分位差 缩放。 数值数组
按数值缩放。 表
使用表中的变量缩放。输入数据 A中的每个表变量都使用缩放表中名称相似的变量的值进行缩放。
'range'二元素行向量(默认为 [0 1])
将数据范围重新缩放至 [a b]形式的区间,其中a < b。
'center'
'mean'(默认值)中心化以使其均值为 0。
'median'中心化以使其中位数为 0。 数值数组
按数值平移中心。该数组必须具有与输入 A 兼容的大小。表
使用表中的变量平移中心。输入数据 A中的每个表变量使用中心化表中名称相似的变量中的值进行中心化。要返回函数用于归一化数据的形参,请指定 C 和 S 输出实参。
N = normalize(___,'center',centertype,'scale',scaletype) 同时使用 'center' 和 'scale' 方法。只有这两种方法可以一起使用。如果未指定 centertype 或 scaletype,则 normalize 将使用该方法的默认方法类型(中心化以使均值为 0 并按标准差缩放)。
此语法支持使用任意中心化和缩放类型同时执行这两个方法。例如,N = normalize(A,'center','median','scale','mad')。您也可以使用此语法指定以前计算的归一化的中心化和缩放值 C 和 S。例如,用 [N1,C,S] = normalize(A1) 归一化一个数据集并保存参数。然后,用 N2 = normalize(A2,'center',C,'scale',S) 对不同数据集重用这些参数。
N = normalize(___,Name,Value) 使用一个或多个名称-值参数指定用于平滑处理的其他参数。例如,当 A 是表或时间表时,normalize(A,'DataVariables',datavars) 对 datavars 指定的变量进行归一化。
[N,C,S] = normalize(___) 还返回用于执行归一化的中心化和缩放值 C 和 S。然后,您可以通过 N = normalize(A2,'center',C,'scale',S) 使用 C 和 S 中的值来归一化不同输入数据。
N— 归一化值归一化值,以数组、表或时间表形式返回。
除非
ReplaceValues的值为false,否则N与A的大小相同。如果ReplaceValues的值是false,则N的宽度是输入数据宽度和指定的数据变量数目之和。
normalize通常对输入表和时间表的所有变量进行运算,以下情况除外:
如果指定
DataVariables,则normalize只对指定的变量执行运算。如果您使用语法
normalize(T,'center',C,'scale',S)来使用先前计算的参数C和S来归一化表或时间表T,则normalize会自动使用C和S中的变量名称来确定要对其进行运算的T中的数据变量。
C— 中心化值中心化值,以数组或表形式返回。
当
A是数组时,normalize将C和S以数组形式返回,满足N = (A - C) ./ S。C中的每个值都是用于在指定维度上执行归一化的中心化值。例如,如果A是 10×10 数据矩阵,并且normalize在第一个维度上执行运算,则C是 1×10 向量,其中包含A中每列的中心化值。当
A是表或时间表时,normalize以表形式返回C和S,其中包含归一化的每个表变量的中心化值和缩放值的表,即N.Var = (A.Var - C.Var) ./ S.Var。C和S的表变量名称与输入中对应的表变量匹配。C中的每个变量都包含用于归一化A中名称相似的变量的中心化值。
S— 缩放值缩放值,以数组或表形式返回。
当
A是数组时,normalize将C和S以数组形式返回,满足N = (A - C) ./ S。S中的每个值都是用于在指定维度上执行归一化的缩放值。例如,如果A是 10×10 数据矩阵,并且normalize在第一个维度上执行运算,则S是 1×10 向量,其中包含A中每列的缩放值。当
A是表或时间表时,normalize以表形式返回C和S,其中包含归一化的每个表变量的中心化值和缩放值的表,即N.Var = (A.Var - C.Var) ./ S.Var。C和S的表变量名称与输入中对应的表变量匹配。S中的每个变量都包含用于归一化A中名称相似的变量的缩放值。
Z 值
z 值以标准差为单位测量数据点与均值的距离。标准化后的数据集均值为 0,标准差为 1,并保留原始数据集的形状属性(相同的偏斜度和峰度)。
对于具有均值 μ 和标准差 σ 的随机变量 X,值 x 的 z 值是 z=(x−μ)/σ.。对于具有均值 ‾‾X 和标准差 S 的采样数据,数据点 x 的 z 值是 z=(x−‾‾X)/S.
P-范数
具有 N 个元素的向量 v 的 p-范数的常规定义是

,其中 p 是任何正的实数值、
Inf或-Inf。p 的一些常见值是 1、2 和Inf。
如果 p 为 1,则所得的 1-范数是向量元素的绝对值之和。
如果 p 为 2,则所得的 2-范数是向量的模或欧几里德长度。
如果 p 为
Inf,则 ‖v‖∞=maxi(∣v(i)∣)。重新缩放
重新缩放通过沿数字线拉伸或压缩点来更改数据集中最小值和最大值之间的距离。数据的 z 分数会保留,因此分布的形状保持不变。
将数据
X重新缩放到任意区间[a b]的方程是
虽然
normalize和 rescale 函数都可以将数据重新缩放到任意区间,但rescale还允许将输入数据裁剪到指定的最小值和最大值。四分位差
数据集的四分位差 (IQR) 说明对值进行排序时中间 50% 的值的范围。如果数据的中位数为 Q2,数据下半部分的中位数为 Q1,数据上半部分的中位数为 Q3,则 IQR = Q3 - Q1。
当数据包含离群值(非常大或非常小的值)时,IQR 通常优于查看全部数据范围,因为 IQR 排除了数据中最大 25% 和最小 25% 的值。
中位数绝对偏差
数据集的中位数绝对偏差 (MAD) 是距数据中位数 ˜X 的绝对偏差的中位数值:MAD=median(∣∣x−˜X∣∣)。因此,MAD 说明数据相对于中位数的变异性。
当数据包含离群值(非常大或非常小的值)时,MAD 通常优于使用数据的标准差,因为标准差对距均值的偏差求平方,从而使离群值的影响过大。相反,少量离群值的偏差不会影响 MAD 的值。
🔥示例
向量和矩阵数据
通过计算 Z 分数来归一化向量和矩阵中的数据。
创建一个向量 v 并计算 Z 分数,从而将数据归一化,使其均值为 0,标准差为 1。
v = 1:5;
N = normalize(v)N = 1×5-1.2649 -0.6325 0 0.6325 1.2649
创建一个矩阵 B 并计算每列的 Z 分数。然后,对每个行进行归一化。
B = magic(3)B = 3×38 1 63 5 74 9 2
N1 = normalize(B)N1 = 3×31.1339 -1.0000 0.3780-0.7559 0 0.7559-0.3780 1.0000 -1.1339
N2 = normalize(B,2)N2 = 3×30.8321 -1.1094 0.2774-1.0000 0 1.0000-0.2774 1.1094 -0.8321
缩放数据
对向量 A 按其标准差进行缩放。
A = 1:5;
Ns = normalize(A,'scale')Ns = 1×50.6325 1.2649 1.8974 2.5298 3.1623
对 A 进行缩放,使其范围在 [0,1] 区间内。
Nr = normalize(A,'range')Nr = 1×50 0.2500 0.5000 0.7500 1.0000
指定方法类型
创建向量 A 并用它的 1-范数对其进行归一化。
A = 1:5;
Np = normalize(A,'norm',1)Np = 1×50.0667 0.1333 0.2000 0.2667 0.3333
对 A 中的数据进行中心化,使其均值为 0。
Nc = normalize(A,'center','mean')Nc = 1×5-2 -1 0 1 2
表变量
创建一个表,其中包含五个人的身高信息。
LastName = {'Sanchez';'Johnson';'Lee';'Diaz';'Brown'};
Height = [71;69;64;67;64];
T = table(LastName,Height)T=5×2 tableLastName Height_________ ______'Sanchez' 71 'Johnson' 69 'Lee' 64 'Diaz' 67 'Brown' 64
按最大身高对身高数据进行归一化。
N = normalize(T,'norm',Inf,'DataVariables','Height')N=5×2 tableLastName Height _________ _______'Sanchez' 1'Johnson' 0.97183'Lee' 0.90141'Diaz' 0.94366'Brown' 0.90141
用相同的参数归一化多个数据集
归一化数据集,返回计算出的参数值,并重用这些参数以对另一个数据集应用相同的归一化。
创建一个包含两个变量 Temperature 和 WindSpeed 的时间表。然后用同样的变量创建第二个时间表,但使用的采样是一年后收集的。
rng default
Time1 = (datetime(2019,1,1):days(1):datetime(2019,1,10))';
Temperature = randi([10 40],10,1);
WindSpeed = randi([0 20],10,1);
T1 = timetable(Temperature,WindSpeed,'RowTimes',Time1)T1=10×2 timetableTime Temperature WindSpeed___________ ___________ _________01-Jan-2019 35 3 02-Jan-2019 38 20 03-Jan-2019 13 20 04-Jan-2019 38 10 05-Jan-2019 29 16 06-Jan-2019 13 2 07-Jan-2019 18 8 08-Jan-2019 26 19 09-Jan-2019 39 16 10-Jan-2019 39 20
Time2 = (datetime(2020,1,1):days(1):datetime(2020,1,10))';
Temperature = randi([10 40],10,1);
WindSpeed = randi([0 20],10,1);
T2 = timetable(Temperature,WindSpeed,'RowTimes',Time2)T2=10×2 timetableTime Temperature WindSpeed___________ ___________ _________01-Jan-2020 30 14 02-Jan-2020 11 0 03-Jan-2020 36 5 04-Jan-2020 38 0 05-Jan-2020 31 2 06-Jan-2020 33 17 07-Jan-2020 33 14 08-Jan-2020 22 6 09-Jan-2020 30 19 10-Jan-2020 15 0
将第一个时间表归一化。指定三个输出:归一化后的表,以及函数用于执行归一化的中心化和缩放参数值 C 和 S。
[T1_norm,C,S] = normalize(T1)T1_norm=10×2 timetableTime Temperature WindSpeed___________ ___________ _________01-Jan-2019 0.57687 -1.4636 02-Jan-2019 0.856 0.92885 03-Jan-2019 -1.4701 0.92885 04-Jan-2019 0.856 -0.4785 05-Jan-2019 0.018609 0.36591 06-Jan-2019 -1.4701 -1.6044 07-Jan-2019 -1.0049 -0.75997 08-Jan-2019 -0.26052 0.78812 09-Jan-2019 0.94905 0.36591 10-Jan-2019 0.94905 0.92885
C=1×2 tableTemperature WindSpeed___________ _________28.8 13.4
S=1×2 tableTemperature WindSpeed___________ _________10.748 7.1056
现在使用第一个归一化的参数值来归一化第二个时间表 T2。此方法确保 T2 中的数据以与 T1 相同的方式中心化并缩放。
T2_norm = normalize(T2,"center",C,"scale",S)T2_norm=10×2 timetableTime Temperature WindSpeed___________ ___________ _________01-Jan-2020 0.11165 0.084441 02-Jan-2020 -1.6562 -1.8858 03-Jan-2020 0.66992 -1.1822 04-Jan-2020 0.856 -1.8858 05-Jan-2020 0.2047 -1.6044 06-Jan-2020 0.39078 0.50665 07-Jan-2020 0.39078 0.084441 08-Jan-2020 -0.6327 -1.0414 09-Jan-2020 0.11165 0.78812 10-Jan-2020 -1.284 -1.8858
默认情况下,normalize 对 T2 中也存在于 C 和 S 中的全部变量进行操作。要归一化 T2 中的变量子集,请使用 DataVariables 名称-值参数指定要对其进行操作的变量。您指定的变量子集必须出现在 C 和 S 中。
将 WindSpeed 指定为要对其进行操作的数据变量。normalize 对该变量进行操作并原样返回 Temperature。
T2_partial = normalize(T2,"center",C,"scale",S,"DataVariables","WindSpeed")T2_partial=10×2 timetableTime Temperature WindSpeed___________ ___________ _________01-Jan-2020 30 0.084441 02-Jan-2020 11 -1.8858 03-Jan-2020 36 -1.1822 04-Jan-2020 38 -1.8858 05-Jan-2020 31 -1.6044 06-Jan-2020 33 0.50665 07-Jan-2020 33 0.084441 08-Jan-2020 22 -1.0414 09-Jan-2020 30 0.78812 10-Jan-2020 15 -1.8858
#### 防伪水印——左手の明天 ####
💗 大家好🤗🤗🤗,我是左手の明天!好久不见💗
💗今天开启新的系列——重新定义matlab强大系列💗
📆 最近更新:2023 年 05 月 25 日,左手の明天的第 286 篇原创博客
📚 更新于专栏:matlab
#### 防伪水印——左手の明天 ####