198.打家劫舍

教程视频：https://www.bilibili.com/video/BV1Te411N7SX
在这里插入图片描述
思路：
1、dp[i]定义：到第 i 间时能拿到的最大金额（此时房间号从0开始）
2、递推公式：当前dp[i]可从两个渠道获得：1、不拿nums[i]；2、拿nums[i]。所以递推公式为dp[i]=Math.max(dp[i-1], dp[i-2]+nums[i]);
3、dp数组初始化：dp[0]=nums[0];dp[1]=Math.max(nums[0], nums[1]);（注意nums长度）
4、遍历顺序：当前金额由前面的金额决定，正序遍历房间
5、打印验证

解法一：动态规划

class Solution {public int rob(int[] nums) {int[] dp = new int[nums.length];//初始化dp[0]=nums[0];if(nums.length<2){return dp[0];}else{dp[1]=Math.max(nums[1],nums[0]);}for(int j=2;j<dp.length;j++){dp[j]=Math.max(dp[j-1], dp[j-2]+nums[j]);}return dp[dp.length-1];}
}// 优化空间 dp数组只用3格空间 记录与当前计算相关的前两个结果和当前结果
class Solution {public int rob(int[] nums) {int[] dp = new int[3];//初始化if(nums.length==1){return nums[0];}else if(nums.length==2){return Math.max(nums[1],nums[0]);}dp[0]=nums[0];dp[1]=Math.max(nums[1],nums[0]);for(int j=2;j<nums.length;j++){dp[2]=Math.max(dp[1], dp[0]+nums[j]);dp[0]=dp[1];dp[1]=dp[2];}return dp[2];}
}// 统一处理
class Solution {public int rob(int[] nums) {int[] dp = new int[3];for(int i=0;i<nums.length;i++){dp[2]=Math.max(dp[1], dp[0]+nums[i]);dp[0]=dp[1];        dp[1]=dp[2]; }return dp[2];}
}

213.打家劫舍II

教程视频：https://www.bilibili.com/video/BV1oM411B7xq
在这里插入图片描述
思路：
将环形问题转化为线性问题。本题可将环形问题分解为取第一个元素和不取第一个元素两种情况，考虑的长度为nums.length-1。即掐头和去尾，然后使用上一题的思路解决。

解法一：分别掐头和去尾，动态规划

class Solution {public int rob(int[] nums) {int len = nums.length;if (len == 1)return nums[0];int num0 = robLiner(nums, nums.length-1, 0);int num1 = robLiner(nums, nums.length-1, 1);return Math.max(num0, num1);}public int robLiner(int[] nums, int len,int startIndex) {int[] dp = new int[3];for(int i=startIndex;i<len+startIndex;i++){dp[2]=Math.max(dp[1], dp[0]+nums[i]);dp[0]=dp[1];        dp[1]=dp[2]; }return dp[2];}
}

337.打家劫舍III

教程视频：https://www.bilibili.com/video/BV1H24y1Q7sY
在这里插入图片描述

解法一：树的递归遍历+动态规划

思路：

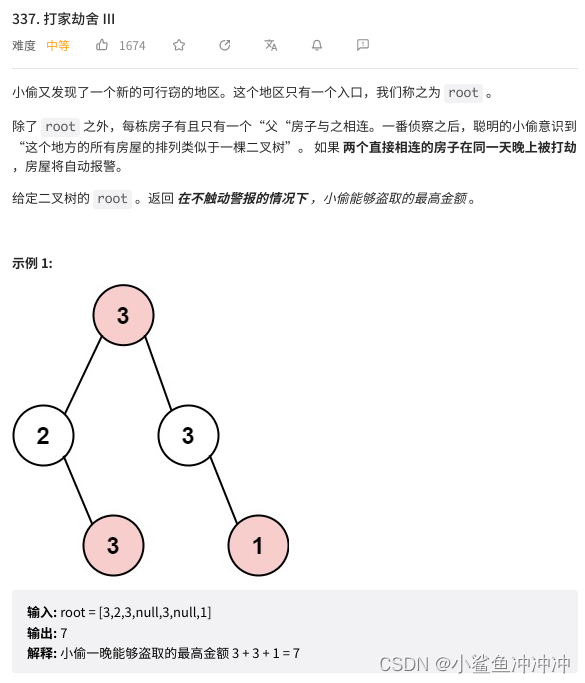
对于树来说，当前节点能不能偷，需要依照其左子树根节点和右子树根节点是否被偷来判断，因此需要采用后序遍历（左右中）。
其次，为了保证计算出当以前节点的为根节点的二叉树能偷的最大金额，需要记录器左右子节点偷和不偷两种状态，因此递归函数的返回值是一个二维数组int[]，其中mid[0]表示不偷的最大值，mid[1]表示偷的最大值。
最后考虑递归逻辑：
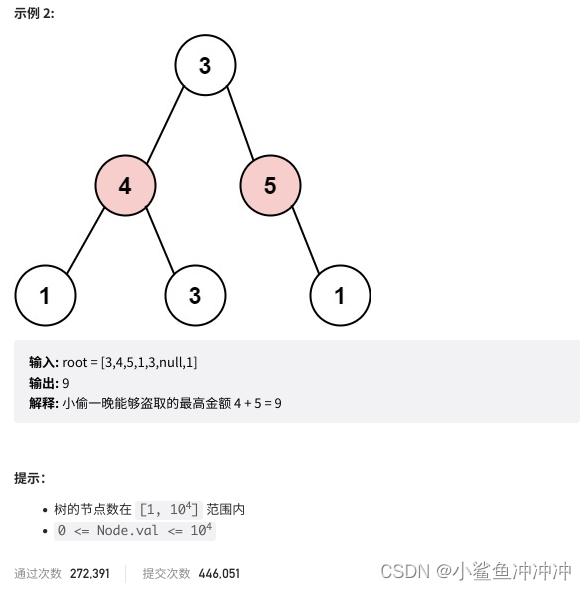
如果是偷当前节点，那么左右孩子就不能偷，mid[1] = left[0]+right[0]+node.val;
如果不偷当前节点，那么左右孩子就可以偷，至于到底偷不偷一定是选一个最大的，所以mid[0] = Math.max(left[0],left[1]) + Math.max(right[0],right[1]);

class Solution {public int rob(TreeNode root) {int[] res = traversal(root);return Math.max(res[0], res[1]);}public int[] traversal(TreeNode node){if(node==null)return new int[2];int[] left = traversal(node.left);int[] right = traversal(node.right);int[] mid = new int[2];mid[0] = Math.max(left[0],left[1])+Math.max(right[0],right[1]); //不偷nodemid[1] = left[0]+right[0]+node.val; //偷nodereturn mid;}
}